
计算机图形学曲线
在计算机图形学中,我们经常需要在屏幕上绘制不同类型的对象。对象并非总是平坦的,我们需要多次绘制曲线来绘制对象。
曲线的类型
曲线是无限大的点集。每个点都有两个邻居,除了端点。曲线可以大致分为三类:**显式曲线、隐式曲线**和**参数曲线**。
隐式曲线
隐式曲线表示通过使用可以测试点是否在曲线上的过程来定义曲线上的点集。通常,隐式曲线由以下形式的隐函数定义:
f(x, y) = 0
它可以表示多值曲线(对于一个 x 值有多个 y 值)。一个常见的例子是圆,其隐式表示为
x2 + y2 - R2 = 0
显式曲线
数学函数 y = f(x) 可以绘制成曲线。这样的函数是曲线的显式表示。显式表示不通用,因为它不能表示垂直线,并且也是单值的。对于每个 x 值,函数通常只计算一个 y 值。
参数曲线
具有参数形式的曲线称为参数曲线。显式和隐式曲线表示仅在已知函数时才能使用。在实践中,使用参数曲线。二维参数曲线具有以下形式:
P(t) = f(t), g(t) 或 P(t) = x(t), y(t)
函数 f 和 g 成为曲线上的任何点的 (x, y) 坐标,当参数 t 在某个区间 [a, b](通常为 [0, 1])内变化时获得这些点。
贝塞尔曲线
贝塞尔曲线是由法国工程师**皮埃尔·贝塞尔**发现的。这些曲线可以在其他点的控制下生成。使用控制点近似切线来生成曲线。贝塞尔曲线可以用数学方式表示为:
$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$
其中 $p_{i}$ 是点集,${B_{i}^{n}}(t)$ 表示伯恩斯坦多项式,由以下公式给出:
$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$
其中**n**是多项式的次数,**i**是索引,**t**是变量。
最简单的贝塞尔曲线是从点 $P_{0}$ 到 $P_{1}$ 的直线。二次贝塞尔曲线由三个控制点确定。三次贝塞尔曲线由四个控制点确定。
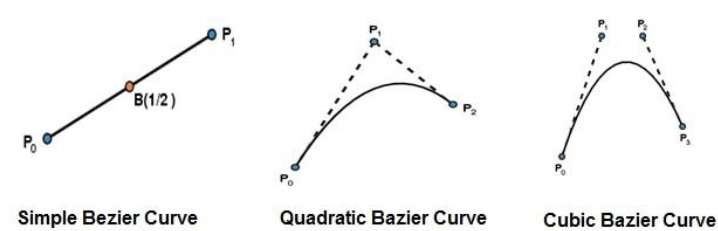
贝塞尔曲线的性质
贝塞尔曲线具有以下性质:
它们通常遵循控制多边形的形状,控制多边形由连接控制点的线段组成。
它们始终穿过第一个和最后一个控制点。
它们包含在其定义控制点的凸包中。
定义曲线段的多项式的次数比定义多边形点的数量少 1。因此,对于 4 个控制点,多项式的次数为 3,即三次多项式。
贝塞尔曲线通常遵循定义多边形的形状。
端点处切向量的方向与由第一段和最后一段确定的向量方向相同。
贝塞尔曲线的凸包属性确保多项式平滑地遵循控制点。
任何直线与贝塞尔曲线的交点次数不超过它与控制多边形的交点次数。
它们在仿射变换下是不变的。
贝塞尔曲线表现出全局控制,这意味着移动一个控制点会改变整个曲线的形状。
给定的贝塞尔曲线可以在点 t=t0 处细分为两个贝塞尔段,这两个段在对应于参数值 t=t0 的点处连接在一起。
B 样条曲线
由伯恩斯坦基函数生成的贝塞尔曲线灵活性有限。
首先,指定的polygon顶点数固定了定义曲线的所得多项式的阶数。
第二个限制特性是混合函数的值在整个曲线上对所有参数值都非零。
B 样条基包含伯恩斯坦基作为特例。B 样条基是非全局的。
B 样条曲线定义为控制点 Pi 和 B 样条基函数 $N_{i,}$ k (t) 的线性组合,由下式给出
$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$
其中,
{$p_{i}$: i=0, 1, 2….n} 是控制点
k 是 B 样条曲线的曲线段的阶数。阶数 k 表示曲线由 k - 1 次的分段多项式段组成,
the $N_{i,k}(t)$ 是“归一化 B 样条混合函数”。它们由阶数 k 和通常称为“节点序列”的实数的非递减序列描述。
$${t_{i}:i = 0, ... n + K}$$
Ni, k 函数描述如下:
$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$
如果 k > 1,则
$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$
并且
$$t \: \epsilon \: [t_{k-1},t_{n+1})$$
B 样条曲线的性质
B 样条曲线具有以下性质:
对于任何参数值,B 样条基函数的总和为 1。
每个基函数对于所有参数值都为正或零。
除了 k=1 之外,每个基函数都恰好有一个最大值。
曲线的最大阶数等于定义多边形顶点数。
B 样条多项式的次数与定义多边形顶点数无关。
B 样条允许对曲线曲面进行局部控制,因为每个顶点仅在其关联的基函数非零的参数值范围内影响曲线的形状。
曲线表现出降维特性。
曲线通常遵循定义多边形的形状。
任何仿射变换都可以通过将其应用于定义多边形的顶点来应用于曲线。
曲线位于其定义多边形的凸包内。