计算机图形学 - 观察与裁剪

---

---

裁剪在计算机图形学中的主要用途是去除视区之外的对象、线条或线段。观察变换对点相对于观察体积的位置不敏感——尤其是那些在观察者后面的点——因此在生成视图之前必须去除这些点。

点裁剪

从给定窗口裁剪点非常容易。考虑下图，其中矩形表示窗口。点裁剪告诉我们给定点 (X, Y) 是否在给定窗口内；并决定我们是否将使用窗口的最小和最大坐标。

如果 X 位于 Wx1 ≤ X ≤ Wx2 之间，则给定点的 X 坐标在窗口内。同理，如果 Y 位于 Wy1 ≤ Y ≤ Wy2 之间，则给定点的 Y 坐标在窗口内。

线裁剪

线裁剪的概念与点裁剪相同。在线裁剪中，我们将剪掉窗口外部的线段，只保留窗口内部的线段。

Cohen-Sutherland 线裁剪

此算法使用下图所示的裁剪窗口。裁剪区域的最小坐标为 $(XW_{min,} YW_{min})$，裁剪区域的最大坐标为 $(XW_{max,} YW_{max})$。

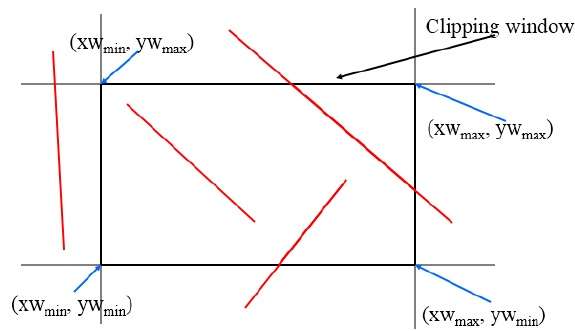
我们将使用 4 位来划分整个区域。这 4 位分别表示区域的顶部、底部、右侧和左侧，如下面的图所示。这里，顶部和左侧位被设置为 1，因为它位于左上角。

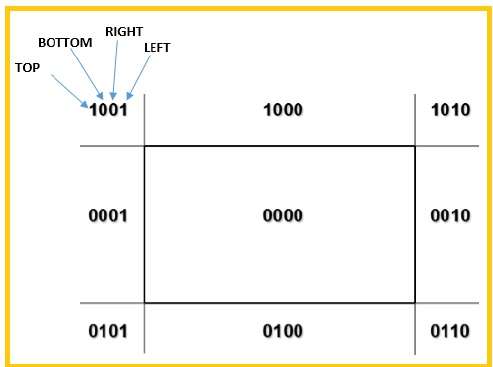
对于直线，存在 3 种可能性：

• 直线可以完全位于窗口内（此直线应被接受）。

• 直线可以完全位于窗口外（此直线将完全从区域中移除）。

• 直线可以部分位于窗口内（我们将找到交点，并仅绘制位于区域内的线段）。

算法

步骤 1 - 为每个端点分配区域代码。

步骤 2 - 如果两个端点的区域代码均为0000，则接受此直线。

步骤 3 - 否则，对两个区域代码执行逻辑与运算。

步骤 3.1 - 如果结果不是0000，则拒绝此直线。

步骤 3.2 - 否则，您需要裁剪。

步骤 3.2.1 - 选择窗口外部的直线端点。

步骤 3.2.2 - 在窗口边界处找到交点（基于区域代码）。

步骤 3.2.3 - 用交点替换端点并更新区域代码。

步骤 3.2.4 - 重复步骤 2，直到我们找到一条被平凡接受或平凡拒绝的裁剪直线。

步骤 4 - 对其他直线重复步骤 1。

Cyrus-Beck 线裁剪算法

此算法比 Cohen-Sutherland 算法更有效率。它采用参数线表示和简单的点积。

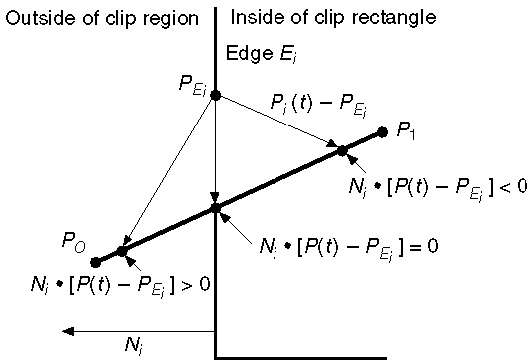
直线参数方程为：

P0P1:P(t) = P0 + t(P1 - P0)

设 N_i 为外法线边 E_i。现在在边 E_i 上选择任意点 P_Ei，则点积 N_i.[P(t) – P_Ei] 决定点 P(t) 是“在裁剪边内”还是“在裁剪边外”或“在裁剪边上”。

如果 N_i.[P(t) – P_Ei] < 0，则点 P(t) 在内部

如果 N_i.[P(t) – P_Ei] > 0，则点 P(t) 在外部

如果 N_i.[P(t) – P_Ei] = 0（交点），则点 P(t) 在边上

N_i.[P(t) – P_Ei] = 0

N_i.[ P₀ + t(P₁ - P₀) – P_Ei] = 0（用 P₀ + t(P₁ - P₀) 替换 P(t)）

N_i.[P₀ – P_Ei] + N_i.t[P₁ - P₀] = 0

N_i.[P₀ – P_Ei] + N_i∙tD = 0（将 D 替换为 [P₁ - P₀]）

N_i.[P₀ – P_Ei] = - N_i∙tD

t 的方程变为：

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

它对于以下条件有效：

• N_i ≠ 0（错误不可能发生）
• D ≠ 0（P₁ ≠ P₀）
• N_i∙D ≠ 0（P₀P₁ 不平行于 E_i）

多边形裁剪（Sutherland Hodgman 算法）

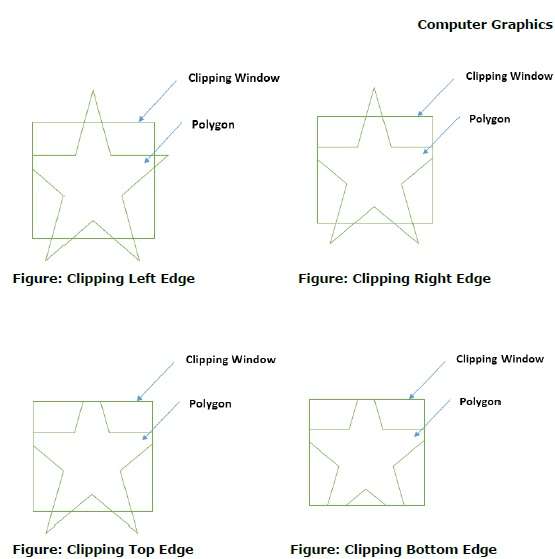
也可以通过指定裁剪窗口来裁剪多边形。Sutherland Hodgeman 多边形裁剪算法用于多边形裁剪。在此算法中，多边形的所有顶点都针对裁剪窗口的每条边进行裁剪。

首先，多边形针对多边形窗口的左边缘进行裁剪，以获得多边形的新顶点。这些新顶点用于针对裁剪窗口的右边缘、上边缘、下边缘裁剪多边形，如下面的图所示。

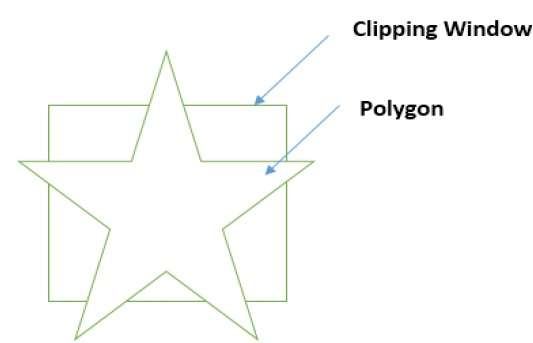
在处理多边形与裁剪窗口的边缘时，如果边缘不完全位于裁剪窗口内，则会找到一个交点，并且从交点到外部边缘的部分边缘会被裁剪。下图显示了左、右、上和下边缘裁剪：

文本裁剪

在计算机图形学中，使用各种技术来提供文本裁剪。它取决于用于生成字符的方法和特定应用程序的要求。文本裁剪有三种方法，如下所示：

• 全部或无字符串裁剪
• 全部或无字符裁剪
• 文本裁剪

下图显示了全部或无字符串裁剪：

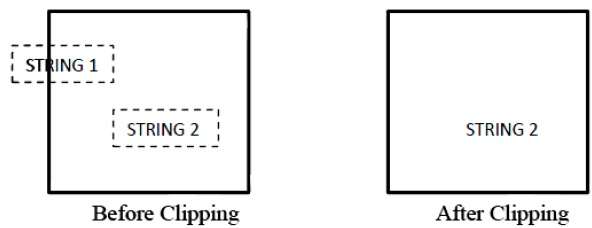
在全部或无字符串裁剪方法中，我们根据裁剪窗口保留整个字符串或拒绝整个字符串。如上图所示，STRING2 完全位于裁剪窗口内，因此我们保留它；STRING1 仅部分位于窗口内，因此我们拒绝它。

下图显示了全部或无字符裁剪：

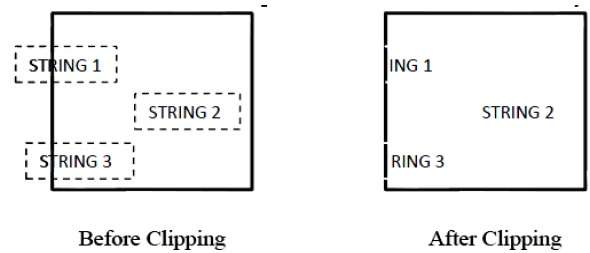
此裁剪方法基于字符而不是整个字符串。在此方法中，如果字符串完全位于裁剪窗口内，则我们保留它。如果它部分位于窗口外，则：

• 您仅拒绝字符串的外部部分

• 如果字符位于裁剪窗口的边界上，则我们丢弃该整个字符并保留其余字符串。

下图显示了文本裁剪：

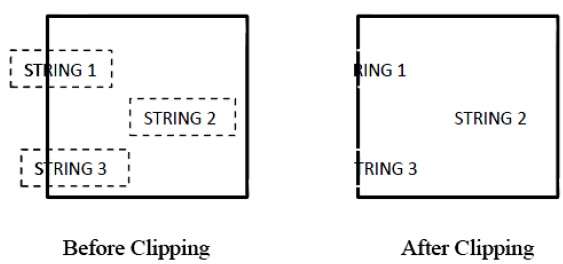
此裁剪方法基于字符而不是整个字符串。在此方法中，如果字符串完全位于裁剪窗口内，则我们保留它。如果它部分位于窗口外，则

• 您仅拒绝字符串的外部部分。

• 如果字符位于裁剪窗口的边界上，则我们仅丢弃字符的窗口外部部分。

位图图形

位图是描述图像的像素集合。它是计算机图形的一种类型，计算机使用它来存储和显示图片。在这种类型的图形中，图像逐位存储，因此被称为位图图形。为了更好地理解，让我们考虑以下示例，其中我们使用位图图形绘制笑脸。

现在我们将了解此笑脸如何在计算机图形学中逐位存储。

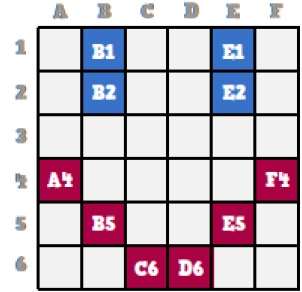
仔细观察原始笑脸，我们可以看到有两条蓝线，在上图中分别表示为 B1、B2 和 E1、E2。

同样，笑脸分别使用 A4、B5、C6、D6、E5 和 F4 的组合位表示。

位图图形的主要缺点是：

• 我们无法调整位图图像的大小。如果您尝试调整大小，像素会变得模糊。

• 彩色位图可能非常大。