数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++中计算内接于等边三角形的不同矩形的数量
我们有一个边长为n的等边三角形。目标是计算在三角形内可以存在的不同矩形的数量，矩形的水平边平行于底边。所有矩形的端点都与图中所示的点相接触。
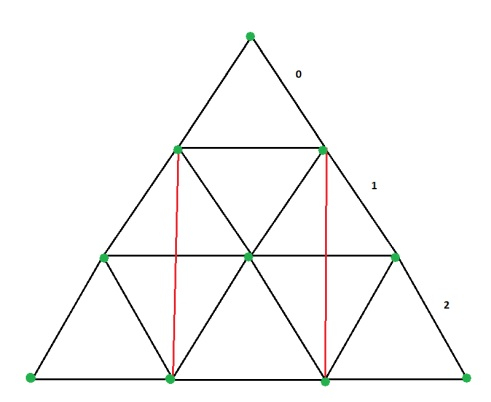
让我们通过例子来理解
输入 − 边长=3
输出 − 内接于等边三角形的不同矩形的数量为 − 1
解释 − 上图显示了该矩形。
输入 − 边长=10
输出 − 内接于等边三角形的不同矩形的数量为 − 200
下面程序中使用的算法如下
从上图可以看出，水平边存在于交替层级的点之间。
点的数量可以从第0层到第1层，第1层到第2层……第n层到第n+1层计算。
输入边长作为整数变量，并将其传递给函数以进行进一步处理。
将计数、临时变量和检查作为临时变量。
如果边长是奇数，则启动循环 FOR i 从 sides - 1 到 i 大于 1
在循环内，如果 i & 1，则将 temp 设置为 (sides - i)/2，将 check 设置为 (i * (i + 1))/2，并将 count 设置为 check * temp；否则，将 temp 设置为 ((sides - 1) - i)/2，并将 check 设置为 (i * (i + 1))/2，并将 count 设置为 check * temp。
否则，如果边长是偶数，则启动另一个循环 FOR，i 从 sides - 1 到 i 大于 1。
在循环内，如果 i & 1，则将 temp 设置为 ((sides - 1) - i ) / 2，将 check 设置为 (i * (i + 1)) / 2，并将 count 设置为 check * temp；否则，将 temp 设置为 (sides - i) / 2，将 check 设置为 (i * (i + 1)) / 2，并将 count 设置为 check * temp。
返回 count
打印结果。
示例
#include <iostream>
using namespace std;
int rec_inside_equi(int sides){
int count = 0, temp, check;
if(sides%2 != 0){
for(int i = sides - 2; i >= 1; i--){
if (i & 1){
temp = (sides - i) / 2;
check = (i * (i + 1)) / 2;
count += check * temp;
}
else{
temp = ((sides - 1) - i) / 2;
check = (i * (i + 1)) / 2;
count += check * temp;
}
}
}
else{
for(int i = sides - 2; i >= 1; i--){
if (i & 1){
temp = ((sides - 1) - i) / 2;
check = (i * (i + 1)) / 2;
count += check * temp;
}
else{
temp = (sides - i) / 2;
check = (i * (i + 1)) / 2;
count += check * temp;
}
}
}
return count;
}
int main(){
int sides = 4;
cout<<"Count of distinct rectangles inscribed in an equilateral triangle are: "<<rec_inside_equi(sides);
return 0;
}输出
如果我们运行上面的代码，它将生成以下输出：
Count of distinct rectangles inscribed in an equilateral triangle are: 4
88 次浏览
