数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
安卓
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会科学
时尚学
法学使用拓扑排序在图中检查环路
在有向无环图中，我们可以使用拓扑排序按照线性顺序对顶点进行排序。
拓扑排序仅适用于有向无环图。在有向无环图 (DAG) 中，可能有多个拓扑排序。
我们考虑一个 C++ 程序，它将执行拓扑排序以检查图中的环路。
例如
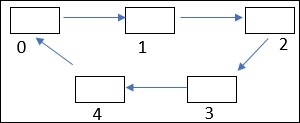
算法
Topological Sort: Begin Declare topo_sort(int *v, int T_S[][5], int i) function a = new NodeInfo. a->n = i a->S_Time = cn. Call push_node(a) function to insert data. v[i] = 1. for (int j = 0; j < 5; j++) if (T_S[i][j] == 0 || (T_S[i][j] == 1 && v[j] == 1)) then continue. else if(T_S[i][j] == 1 && v[j] == 0) then cn++. Call topo_sort(v,T_S, j) function. cn++. a = pop(). a->L_Time = cn. Store_Node(a). End.
示例
#include<iostream>
#include<conio.h>
using namespace std;
struct NodeInfo {
int n;
int L_Time, S_Time;
}
*a = NULL;
struct Node {
NodeInfo *ptr;
Node *nxt;
}
*t = NULL, *b = NULL, *npt = NULL;
struct Node_Link {
Node_Link *lk;
NodeInfo *ptr1;
}
*hd = NULL, *m = NULL, *n = NULL, *npt1 = NULL;
int cn = 0;
bool flag = false;
void push_node(NodeInfo *pt) { //insert data
npt = new Node;
npt->ptr = pt;
npt->nxt = NULL;
if (t == NULL) {
t = npt;
} else {
npt->nxt = t;
t = npt;
}
}
NodeInfo *pop() {
if (t == NULL) {
cout<<"underflow\n";
} else {
b = t;
t = t->nxt;
return(b->ptr);
delete(b);
}
}
void Store_Node(NodeInfo *pt1) { //store data
npt1 = new Node_Link;
npt1->ptr1 = pt1;
npt1->lk = NULL;
if (cn == 0) {
hd = npt1;
m = hd;
m->lk = NULL;
cn++;
} else {
m = hd;
npt1->lk = m;
hd = npt1;
}
}
void delete_node(int x) { //delete node
m = hd;
if ((m->ptr1)->n == x) {
hd = hd->lk;
delete(m);
} else {
while ((m->ptr1)->n != x && m->lk != NULL) {
n = m;
m = m->lk;
}
if ((m->ptr1)->n == x) {
n->lk = m->lk;
delete(m);
} else if (m->lk == NULL) {
flag = true;
cout<<"There is no circle in this graph\n";
}
}
}
void topo_sort(int *v, int T_S[][5], int i) { //performing topological sort
a = new NodeInfo;
a->n = i;
a->S_Time = cn;
push_node(a);
v[i] = 1;
for (int j = 0; j < 5; j++) {
if (T_S[i][j] == 0 || (T_S[i][j] == 1 && v[j] == 1))
continue;
else if(T_S[i][j] == 1 && v[j] == 0) {
cn++;
topo_sort(v,T_S,j);
}
}
cn++;
a = pop();
a->L_Time = cn;
Store_Node(a);
return;
}
void topologic_sort(int *v, int T_S[][5], int i) {
v[i] = 1;
delete_node(i);
for (int j = 0; j < 5; j++) {
if (T_S[i][j] == 0 || (T_S[i][j] == 1 && v[j] == 1)) {
continue;
} else if(T_S[i][j] == 1 && v[j] == 0) {
topologic_sort(v, T_S, j);
}
}
return;
}
void Insert_Edge(int T_S[][5], int source, int destination) { // insert the value of edge.
T_S[source][destination] = 1;
return;
}
int main() {
int v[5], T_S[5][5], T_S_N[5][5], cn = 0, a, b;
for (int i = 0; i < 5; i++) {
v[i] = 0;
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
T_S[i][j] = 0;
}
}
while (cn < 5) {
cout<<"Enter the source: ";
cin>>a;
cout<<"Enter the destination: ";
cin>>b;
cout<<endl;
Insert_Edge(T_S, a, b);
cn++;
}
topo_sort(v, T_S, 0);
for (int i = 0; i < 5; i++) {
v[i] = 0;
for (int j = 0; j < 5; j++) {
T_S_N[j][i] = T_S[i][j];
}
}
if (hd != NULL) {
topologic_sort(v, T_S_N, (hd->ptr1)->n);
if (flag == false) {
cout<<"There is a cycle in this graph...\n";
}
}
getch();
}输出
Enter the source: 0 Enter the destination: 1 Enter the source: 1 Enter the destination: 2 Enter the source: 2 Enter the destination: 3 Enter the source: 3 Enter the destination: 4 Enter the source: 4 Enter the destination: 0 There is a cycle in this graph...
更新于： 30-7-2019
326 次浏览
广告