圆柱体

---

引言

绕平行于其自身的固定直线旋转线段所得到的圆柱体称为旋转圆柱体。在我们的日常生活中，我们熟悉许多圆柱形物体。传统上，圆柱体或圆柱形结构的定义包括一个具有棱柱形形状和圆形底部的三维实体，例如铅笔、压路机和管道是一些基本的圆柱体示例。

这是最基本的曲线几何形状之一。这种传统观点在解决简单的几何问题时仍然有用。然而，从复杂的数学角度来看，圆柱面被视为无限弯曲的曲面。如今，许多现代几何和拓扑领域都遵循这一概念。在本文中，我们将讨论与圆柱形结构相关的特性、变体和公式。

今天我们将讨论圆柱体的属性、形状中使用的参数，并处理一些问题。

圆柱体

它由平行的圆盘组成；我们可以说许多圆盘构成一个圆柱体。如果我们连接所有圆盘的中心，连接轴的线段就是圆柱体的高度。

• 从顶部看，圆柱体看起来像一个圆。

• 圆柱体的正面视图看起来像一个矩形。它具有曲线，不像立方体和长方体那样是直线。

圆柱体的类型

• 椭圆柱体 - 椭圆柱体结构是一个具有椭圆形底部的圆柱体。

• 直圆柱体 - 通过绕其一边作为轴旋转矩形，创建了一个称为直圆柱体的物体。如果轴（矩形的一边）垂直于半径 (r)，则该圆柱体称为直圆柱体。圆柱体的高度 (h) 是其顶部和底部的圆形面之间的距离，这两个圆形面彼此平行。

• 斜圆柱体 - 斜圆柱体是指圆形面侧向而不是彼此叠加，并且轴与底面形成非直角的圆柱体。

• 空心圆柱体 - 空心圆柱体是一种圆柱形结构，其内外表面直径存在差异，内部为空心。由于内外径可变，因此它们可以具有不同的内外侧表面积。

圆柱体的公式

在三维几何中，圆柱体占据的整个空间称为其面积。圆柱体的面积包括两个圆形底部的总表面积加上侧表面积。两个圆形底部之间有一个弯曲的或侧表面。当弯曲的表面打开时，表示一个矩形。高度、半径、轴、边和底是用于计算圆柱体面积的许多变量。圆柱体的半径等于其两个圆形边之间的距离。两个圆形边之间的垂直距离称为圆柱体的高度，其半径可以写成 (r)。圆柱体的高度指定为 (h)

圆柱形结构的表面积可分为两类。

• 曲面面积 (CSA)

• 总表面积 (TSA)

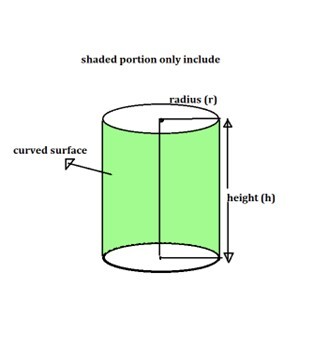
曲面面积或侧表面积

侧表面积是曲面面积的另一个名称。曲面的面积是圆柱形结构的面积，不包括其圆形底部的面积。

一般情况下，面积使用平方厘米、平方米等平方单位来测量。

如果打开圆柱体的曲面面积，可以看到一个矩形。

曲面面积上的两个圆形边缘的大小可能与圆的直径相符。

圆的周长可以使用公式 2r 计算。

因此，矩形的长度（打开曲面后）为 2r，其宽度为 (h)。因此，曲面的面积为 2Πrh。

所以，公式如下所示：

$$\mathrm{圆柱体的曲面面积 = 2Πrh 平方单位.}$$

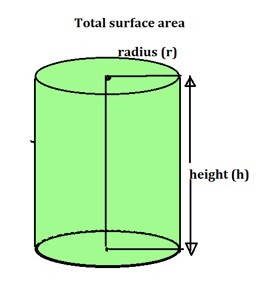
总表面积

圆柱体的总表面积是两个圆的面积和弯曲或侧表面的面积之和，其公式如下：

总表面积 = 两个圆的面积 + 曲面面积

$$\mathrm{=2×Πr^2+2Πrh }$$

$$\mathrm{ =2Πr(r+h) 平方单位}$$

体积

每个实体或三维形状都具有占据一定空间的体积。圆柱体在任何三维平面中占据的区域就是它的体积。圆柱体的容量表示其内部可能容纳多少水。

$$\mathrm{圆柱体的体积 = Πr^2 h 立方单位}$$

例题

1)如果圆柱体的高度为 12 厘米，圆柱体的体积为 8478 立方厘米，那么圆柱体的半径是多少？

答案

已知，圆柱体的高度 (h) = 12 厘米

圆柱体的体积 (v) = 8478 立方厘米

我们知道，

圆柱体的体积 (v) = Πr² h

$$\mathrm{8478 = 3.14×r^2×12}$$

$$\mathrm{8478 = 37.68×r^2}$$

$$\mathrm{225 = r^2}$$

因此，r = 15 厘米

所以圆柱体的半径是 15 厘米。

2)如果水箱的直径和高度分别为 30 厘米和 40 厘米，那么圆柱形水箱的体积是多少？

答案

已知，圆柱形水箱的高度 (h) = 40 厘米

圆柱形水箱的直径 (d) = 30 厘米

所以，圆柱形水箱的半径 (r) = 30/2 = 15 厘米

我们知道，

圆柱体的体积 = Πr² h

$$\mathrm{= 3.14×15×15×40}$$

$$\mathrm{= 28260 立方厘米}$$

3) 半径和高度分别为 7 厘米和 20 厘米的圆柱体的总表面积是多少？

答案

已知：

圆柱体的半径 (r) = 7 厘米

圆柱体的高度 (h) = 20 厘米

我们知道，

圆柱体的总表面积 = 2Πr(r+h)

$$\mathrm{= 2×3.14×7×(20 +7)}$$

$$\mathrm{ = 1,186.92 平方厘米}$$

所以，圆柱体的表面积是 1,186.92 平方厘米。

结论

圆柱形结构具有零个顶点、两个边、一个曲面和两个底面。它有两个底面，就像棱柱一样。它们的形状可分为四类：空心圆柱形结构、椭圆柱体、直圆柱体和圆柱形结构。圆柱形结构有两个平行的底面，两个底面之间的距离称为其高度。

• 圆柱体的曲面面积 = 2Πrh 平方单位。

• 圆柱体的总表面积 = 两个圆的面积 + 曲面面积

  $$\mathrm{= 2×Πr^2+2Πrh}$$

  $$\mathrm{= 2Πr(r+h) 平方单位}$$

• 圆柱体的体积 = Πr² h 立方单位

常见问题

1. 圆柱体有多少个面？

圆柱体有两个平坦的圆形侧面和一个曲面。因此，它总共有三个面。

2. 圆柱体有顶点吗？

构成圆柱体的两个平行的圆形侧面具有相同的形状。但是，由于其曲率，它没有任何顶点。

3. 还有哪些其他类型的圆柱体？

直圆柱体、斜圆柱体、椭圆柱体和空心圆柱体是四种不同类型的圆柱体。

4. 什么使圆柱体成为一个三维形状？

圆柱体是一个三维形状，两端有两个平行的圆形侧面。一个曲面。没有顶点或边。