直立圆柱体

---

引言

一个三维立体图形称为直立圆柱体。直立圆柱体的两端都有一个封闭的圆形表面，并且互相平行。直立圆柱体也称为直圆柱体。封闭表面上的所有点都与直立圆柱体的轴线等距。在日常生活中，直立圆柱体是最常见的3D图形。通过堆叠许多圆形的纸片可以创建一个直立圆柱体。因为它与圆形底面成直角，所以被称为直立圆柱体。本教程将涵盖直立圆柱体的表面积、体积和特性。

直立圆柱体

直立圆柱体是由两个平行的底面和一个封闭的曲面构成的三维立体形状，每个底面都类似于圆盘状的圆形。直圆柱体的轴线是连接两个圆形底面中心或穿过其中心的直线。高度，或“ℎ”，代表垂直距离，即圆柱体两个底面之间的距离。直立圆柱体的半径，用“𝑟”表示，是从中心到任一两个底面外边界。因此，两个圆和一个矩形组合起来构成一个直立圆柱体。请看直立圆柱体构造图。

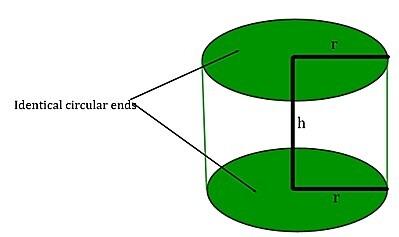
圆柱体的表面积

直立圆柱体的表面所覆盖的面积称为直立圆柱体的表面积。直立圆柱体的表面区域可以分为两类：

直立圆柱体的曲面面积

它也被称为直立圆柱体的侧面积。它是直立圆柱体平行圆形底面之间的空间，由圆柱体的曲面覆盖。因此，求直立圆柱体侧面积的公式为：

$$\mathrm{C.S.A\:=\:2\pi\:rh}$$

直立圆柱体的总表面积

它被描述为圆柱体充满的区域。这个区域包含两个圆和一个曲面。因此，为了计算直立圆柱体的总表面积，我们将两个圆的面积和曲面的面积加起来。

$$\mathrm{T.S.A\:=\:2\pi\:rh\:+\:2\pi\:r^{2}\:=\:2\pi\:r(r\:+\:h)}$$

例题

求半径为1毫米，高为7毫米的圆柱体的侧面积和总表面积。

解：

已知 𝑟 = 1毫米，ℎ = 7毫米

$\mathrm{C.S.A\:=\:2\pi\:rh\:=\:2\:\times\:\frac{22}{7}\:\times\:1\:\times\:7\:=\:44mm^{2}}$

$\mathrm{T.S.A\:=\:2\pi\:r(r\:+\:h)\:=\:2\:\times\:\frac{22}{7}\:\times\:1\:\times\:(1\:+\:7)\:=\:\frac{44\:\times\:8}{7}\:=\:50.285\:mm^{2}}$

圆柱体的体积

直立圆柱体在空间中占据的面积称为体积。直立圆柱体的体积用立方单位表示，如$\mathrm{(m^{3},\:cm^{3},\:in^{3}\:or\:ft^{3})}.$

对于任何高为“ℎ”和半径为“𝑟”的直立圆柱体，其体积公式如下：体积 = 高度 × 圆的面积。因此，求直立圆柱体体积的公式为：

$$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$$

例题

半径为5厘米，高为35厘米的圆柱形水箱的容量是多少？

解：

求直立圆柱体体积的公式为：

$$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$$

已知 $\mathrm{r\:=\:5cm\:,\:h\:=\:35cm}$

因此：

$\mathrm{V\:=\:\pi\:r^{2}h\:=\:\frac{22}{7}\:\times\:5\:\times\:5\:\times\:35\:=\:22\:\times\:125\:=\:2750cm^{3}}$

因此，圆柱形水箱的容量是2750 𝑐𝑚³

解题示例

1. 半径为2米，曲面面积为110平方米的圆柱体的高度是多少？

求直立圆柱体侧面积的公式为

$$\mathrm{C.S.A\:=\:2\pi\:rh}$$

$$\mathrm{110\:=\:2\:\times\:\frac{22}{7}\:\times\:2\:\times\:h}$$

$$\mathrm{h\:=\:\frac{110\:\times\:7}{4\:\times\:22}\:=\frac{35}{4}\:=\:8.75m}$$

因此，直立圆柱体的高度是8.75米

2. 直径为8厘米，高为直径的$\mathrm{\frac{7}{2}}$的圆柱形烧瓶的体积是多少？

解：

求直立圆柱体体积的公式为，$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

已知 $\mathrm{r\:=\:\frac{8}{2}\:=\:4cm\:,\:h\:=\:\frac{7}{2}\:\times\:8cm\:=\:28cm\:V\:=\:\pi\:r^{2}h\:=\:\frac{22}{7}\:\times\:4^{2}\:\times\:28\:=\:22\:\times\:4^{3}\:=\:1408\:cm^{3}}$

因此，圆柱形烧瓶的体积是1408 𝑐𝑚³

3. 半径为7米，高为20米的圆柱形帐篷需要多大面积的篷布？

解：

圆柱形帐篷如下：

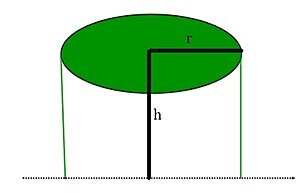
帐篷的总表面积为：

$\mathrm{T.S.A\:=\:2\pi\:rh\:+\:\pi\:r^{2}}$

已知，$\mathrm{r\:\:7m,\:h\:=\:20m}$

所需的篷布总面积为

$$\mathrm{=\:2\pi\:rh\:+\:\pi\:r^{2}\:=\:\pi\:r(2h\:+\:r)}$$

$$\mathrm{=\:\frac{22}{7}\:\times\:7(40\:+\:7)\:=\:22\:\times\:47\:=\:1034\:m^{2}}$$

因此，所需的篷布面积是1034 平方米

4. 体积为200立方厘米，高为5厘米的圆柱体的半径是多少？使用𝜋 = 3.14。

解：

求直立圆柱体体积的公式为 $\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

已知 $\mathrm{V\:=\:200cm^{3}\:,\:h\:=\:5cm}$

$$\mathrm{200\:=\:3.14\:\times\:r^{2}\:\times\:5}$$

$$\mathrm{r^{2}\:=\:\frac{200}{15.7}\:=\:\frac{2000}{157}\:=\:12.74}$$

$$\mathrm{r\:=\:\sqrt{12.74}\:=\:3.57cm}$$

5. 如果直立圆柱体的半径为𝑝单位，高为𝑞单位，写出计算其曲面面积、总表面积和体积的公式。

解：

$$\mathrm{C.S.A\:=\:2\pi\:rh\:=\:2\pi\:pq}$$

$$\mathrm{T.S.A\:=\:2\pi\:r(r\:+\:h)\:=\:2\pi\:p(p\:+\:q)}$$

$$\mathrm{V\:=\:\pi\:r^{2}h\:=\:\pi\:p^{2}q}$$

结论

• 求直立圆柱体侧面积的公式为 $\mathrm{C.S.A\:=\:2\pi\:rh}$

• $\mathrm{T.S.A\:=\:2\pi\:rh\:+\:2\pi\:r^{2}\:=\:2\pi\:r(r\:+\:h)}$ 是求直立圆柱体总表面积的公式。

• 求直立圆柱体体积的公式为 $\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

常见问题

1. 你如何称呼圆柱体的边缘？

圆锥、球体和圆柱体没有平坦的侧面，因此它们没有边缘。顶点是两条或多条边汇合的地方。

2. 直立圆柱体的底面是椭圆形吗？

直立圆柱体有两个平坦的底面，三个侧面和一个曲面。

3. 圆柱体可以有多少个维度？

圆柱体源于希腊字母o，罗马化后为kulindros，意思是“滚筒”或“滚筒”，历史上一直是最基本的曲线几何形状之一。它是三维的。

4. 存在多少种不同类型的圆柱体？

两种最常用的液压缸类型是单作用和双作用液压缸。

5. 圆柱体上是否存在平行线？

圆柱体是一种3D立体形状，由两个平行且相同的底面和一个曲面连接而成。这些底面类似于圆盘。圆柱体的轴线是穿过中心或连接两个圆形底面中心的直线。

6. 圆柱体的曲面叫什么？

总表面积是指圆柱体所有侧面的曲面，不包括底面的面积。

7. 圆柱体不是棱柱，为什么？

棱柱不是旋转几何图形，而圆柱体是。棱柱有两个平坦的矩形面和两个多边形作为其两端，而圆柱体有两个平坦的端面和一个曲面。棱柱有多条对角线，而圆柱体没有。