二叉堆的设计与分析

堆有很多种类型，但在本章中，我们将讨论二叉堆。二叉堆是一种数据结构，它看起来类似于一棵完全二叉树。堆数据结构遵循下面讨论的排序属性。通常，堆用数组表示。在本章中，我们用H表示堆。

由于堆的元素存储在数组中，假设起始索引为1，则第i个元素的父节点的位置可以在⌊ i/2 ⌋找到。第i个节点的左孩子和右孩子分别位于2i和2i + 1的位置。

根据排序属性，二叉堆可以进一步分类为最大堆或最小堆。

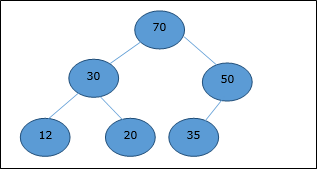
最大堆

在这种堆中，节点的键值大于或等于其最高子节点的键值。

因此，H[Parent(i)] ≥ H[i]

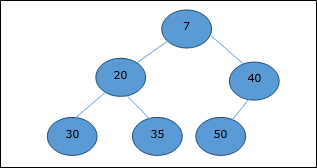
最小堆

在最小堆中，节点的键值小于或等于其最低子节点的键值。

因此，H[Parent(i)] ≤ H[i]

在本例中，基本操作如下所示，针对最大堆。在堆中插入和删除元素需要重新排列元素。因此，需要调用堆化函数。

数组表示

完全二叉树可以用数组表示，使用层序遍历存储其元素。

让我们考虑一个堆（如下所示），它将由数组H表示。

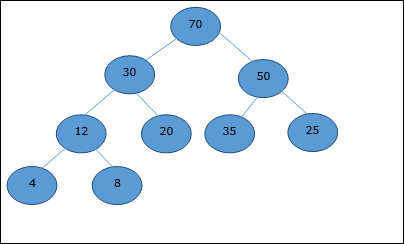
假设起始索引为0，使用层序遍历，元素按如下方式保存在数组中。

在本例中，堆上的操作针对最大堆进行表示。

要查找索引为i的元素的父节点的索引，使用以下算法Parent (numbers[], i)。

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

可以使用以下算法Left-Child (numbers[], i)查找索引为i的元素的左孩子的索引。

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL 

可以使用以下算法Right-Child(numbers[], i)查找索引为i的元素的右孩子的索引。

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL