动态规划

动态规划方法类似于分治法，将问题分解成越来越小的子问题。但与分治法不同的是，这些子问题不是独立解决的。相反，这些较小子问题的结果会被记住并用于类似的或重叠的子问题。

大多数情况下，动态规划算法用于解决优化问题。在解决手头的子问题之前，动态算法会尝试检查先前解决的子问题的结果。子问题的解被组合起来以获得最佳最终解。因此，这种范例被称为自底向上方法。

所以我们可以得出结论：

• 问题应该能够被分解成更小的重叠子问题。

• 可以使用较小子问题的最优解来获得最终的最优解。

• 动态算法使用记忆化。

然而，在一个问题中，两个主要属性可以表明给定的问题可以使用动态规划来解决。它们是：

重叠子问题

与分治法类似，动态规划也组合子问题的解。它主要用于一个子问题的解需要重复使用的地方。计算出的解存储在一个表中，因此不必重新计算。因此，当存在重叠子问题时，需要这种技术。

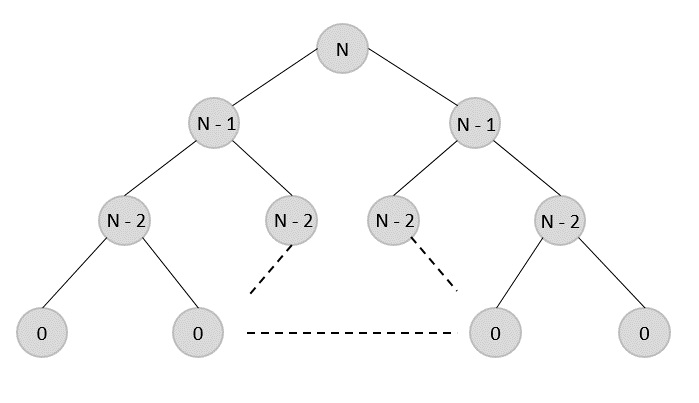
例如，二分查找没有重叠子问题。而斐波那契数的递归程序有很多重叠子问题。

最优子结构

如果给定问题的最优解可以使用其子问题的最优解获得，则给定问题具有最优子结构属性。

例如，最短路径问题具有以下最优子结构属性：

如果节点x位于从源节点u到目标节点v的最短路径中，则从u到v的最短路径是从u到x的最短路径和从x到v的最短路径的组合。

像Floyd-Warshall和Bellman-Ford这样的标准全对最短路径算法是动态规划的典型例子。

动态规划方法的步骤

动态规划算法的设计遵循以下四个步骤：

• 描述最优解的结构。

• 递归地定义最优解的值。

• 计算最优解的值，通常以自底向上的方式。

• 根据计算出的信息构造最优解。

动态规划与贪心算法与分治法的比较

与解决局部优化的贪心算法相比，动态算法的目标是对问题进行全局优化。

与分治算法（其中解被组合以获得全局解）相比，动态算法使用较小子问题的输出，然后尝试优化较大的子问题。动态算法使用记忆化来记住已解决子问题的输出。

动态规划的例子

以下计算机问题可以使用动态规划方法解决：

• 矩阵链乘法

• Floyd-Warshall算法

• 0-1背包问题

• 最长公共子序列算法

• 旅行商问题（动态规划）

动态规划可以自顶向下和自底向上两种方式使用。当然，大多数情况下，参考之前的解输出比重新计算在CPU周期方面更便宜。