最大团

Table of content
上一页
下一页

在一个无向图中，团是一个给定图的完全子图。完全子图意味着这个子图的所有顶点都连接到这个子图的所有其他顶点。

最大团问题是寻找图的最大团的计算问题。最大团用于许多现实世界的问题。

让我们考虑一个社交网络应用程序，其中顶点代表人们的个人资料，边代表图中的相互认识。在这个图中，团代表一群彼此都认识的人。

为了找到最大团，可以系统地检查所有子集，但是这种蛮力搜索对于包含几十个以上顶点的网络来说过于耗时。

最大团算法

寻找图的最大团的算法相对简单。该过程的步骤如下：

步骤1：将一个图作为算法的输入，该图具有非空的顶点集和边集。

步骤2：创建一个输出集，如果边构成图的团，则将它们添加到输出集中。

步骤3：迭代地重复步骤2，直到检查图的所有顶点，并且列表不再形成团。

步骤4：然后回溯输出集以检查哪个团具有最大边数。

伪代码

Algorithm: Max-Clique (G, n, k)
S := ф
for i = 1 to k do
   t := choice (1…n) 
   if t є S then
      return failure
   S := S U t 
for all pairs (i, j) such that i є S and j є S and i ≠ j do
   if (i, j) is not a edge of the graph then 
      return failure
return success

分析

最大团问题是一个非确定性算法。在这个算法中，我们首先尝试确定一组k个不同的顶点，然后我们尝试测试这些顶点是否构成一个完全图。

没有多项式时间确定性算法可以解决这个问题。这个问题是NP完全的。

示例

看下面的图。这里，包含顶点2、3、4和6的子图构成一个完全图。因此，这个子图是一个团。由于这是所提供图的最大完全子图，因此它是一个4-团。

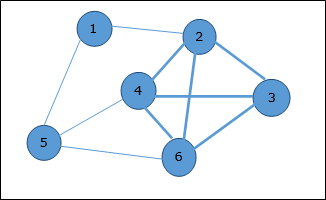
Max Cliques

实现

以下是上述方法在各种编程语言中的实现：

C C++ Java Python
#include <stdio.h>
#define MAX 100
int store[MAX], n;
int graph[MAX][MAX];
int d[MAX];
int max(int a, int b){
   if(a > b){
      return a;
   }
   else{
      return b;
   }
}
int is_clique(int b)
{
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++) {
         if (graph[store[i]][store[j]] == 0) {
            return 0;
         }
      }
   }
   return 1;
}
int maxCliques(int i, int l)
{
   int max_ = 0;
   for (int j = i + 1; j <= n; j++) {
      store[l] = j;
      if (is_clique(l + 1)) {
         max_ = max(max_, l);
         max_ = max(max_, maxCliques(j, l + 1));
      }
   }
   return max_;
}
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
                      { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   printf("Max clique: %d\n", maxCliques(0, 1));
   return 0;
}

输出

Max clique: 3

using namespace std;
#include<iostream>
const int MAX = 100;
// Storing the vertices
int store[MAX], n;
// Graph
int graph[MAX][MAX];
// Degree of the vertices
int d[MAX];
// Function to check if the given set of vertices in store array is a clique or not
bool is_clique(int b)
{
   // Run a loop for all set of edges
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++)
   
      // If any edge is missing
      if (graph[store[i]][store[j]] == 0)
         return false;
   }
   return true;
}
// Function to find all the sizes of maximal cliques
int maxCliques(int i, int l)
{
   // Maximal clique size
   int max_ = 0;
   // Check if any vertices from i+1 can be inserted
   for (int j = i + 1; j <= n; j++) {
      // Add the vertex to store
      store[l] = j;
      // If the graph is not a clique of size k then
      // it cannot be a clique by adding another edge
      if (is_clique(l + 1)) {
   	     // Update max
   	     max_ = max(max_, l);
   	     // Check if another edge can be added
   	     max_ = max(max_, maxCliques(j, l + 1));
   	}
   }
   return max_;
}
// Driver code
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
   				{ 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   cout <<"Max clique: "<<maxCliques(0, 1);
   return 0;
}

输出

Max clique: 3

import java.util.ArrayList;
import java.util.List;
public class MaxCliques {
   static final int MAX = 100;
   static int[] store = new int[MAX];
   static int[][] graph = new int[MAX][MAX];
   static int[] d = new int[MAX];
   static int n;
   // Function to check if the given set of vertices in store array is a clique or not
   static boolean isClique(int b) {
      for (int i = 1; i < b; i++) {
         for (int j = i + 1; j < b; j++)
            if (graph[store[i]][store[j]] == 0)
               return false;
      }
      return true;
   }
   // Function to find all the sizes of maximal cliques
   static int maxCliques(int i, int l) {
      int max_ = 0;
      for (int j = i + 1; j <= n; j++) {
         store[l] = j;
         if (isClique(l + 1)) {
            max_ = Math.max(max_, l);
            max_ = Math.max(max_, maxCliques(j, l + 1));
         }
      }
      return max_;
   }
   // Driver code
public static void main(String[] args) {
   int[][] edges = { { 1, 4 }, { 4, 6 }, { 1, 6 },
           { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = edges.length;
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   System.out.println("Max cliques: " + maxCliques(0, 1));
   }
}

输出

Max cliques: 3

MAX = 100
# Storing the vertices
store = [0] * MAX
n = 0
# Graph
graph = [[0] * MAX for _ in range(MAX)]
# Degree of the vertices
d = [0] * MAX
# Function to check if the given set of vertices in store array is a clique or not
def is_clique(b):
    # Run a loop for all set of edges
    for i in range(1, b):
        for j in range(i + 1, b):
            # If any edge is missing
            if graph[store[i]][store[j]] == 0:
                return False
    return True
# Function to find all the sizes of maximal cliques
def maxCliques(i, l):
    # Maximal clique size
    max_ = 0
    # Check if any vertices from i+1 can be inserted
    for j in range(i + 1, n + 1):
        # Add the vertex to store
        store[l] = j
        # If the graph is not a clique of size k then
        # it cannot be a clique by adding another edge
        if is_clique(l + 1):
            # Update max
            max_ = max(max_, l)
            # Check if another edge can be added
            max_ = max(max_, maxCliques(j, l + 1))
    return max_
# Driver code
def main():
    global n
    edges = [(1, 4), (4, 6), (1, 6),
             (3, 3), (4, 2), (8, 12)]
    size = len(edges)
    n = 6
    for i in range(size):
        graph[edges[i][0]][edges[i][1]] = 1
        graph[edges[i][1]][edges[i][0]] = 1
        d[edges[i][0]] += 1
        d[edges[i][1]] += 1
    print("Max cliques:" ,maxCliques(0, 1))
if __name__ == "__main__":
    main()

输出

Max cliques: 3
打印页面
上一页
下一页
广告