堆排序中的插入操作

Table of content

分析
示例

为了将一个元素插入堆中，新的元素首先被添加到堆的末尾，作为数组的最后一个元素。

插入此元素后，堆属性可能被破坏，因此通过将添加的元素与其父元素进行比较并将添加的元素向上移动一级，与父元素交换位置来修复堆属性。此过程称为 **向上筛选**。

重复比较，直到父元素大于或等于正在筛选的元素。

Algorithm: Max-Heap-Insert (numbers[], key) 
heapsize = heapsize + 1 
numbers[heapsize] = -∞ 
i = heapsize 
numbers[i] = key 
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] 
   exchange(numbers[i], numbers[Parent(numbers[], i)]) 
   i = Parent (numbers[], i)

分析

最初，元素被添加到数组的末尾。如果它违反了堆属性，则元素将与其父元素交换。树的高度为 **log n**。最多需要执行 **log n** 次操作。

因此，此函数的复杂度为 **O(log n)**。

示例

让我们考虑一个最大堆，如下所示，其中需要添加一个新元素 5。

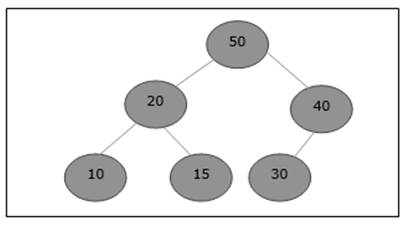
最初，55 将被添加到此数组的末尾。

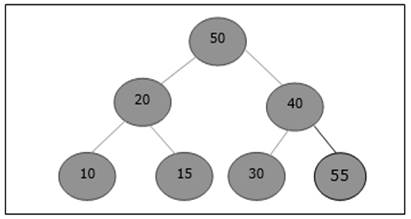
插入后，它违反了堆属性。因此，需要将元素与其父元素交换。交换后，堆如下所示。

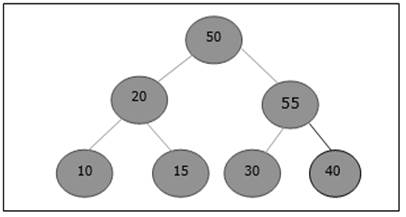
元素再次违反了堆属性。因此，它与其父元素交换。

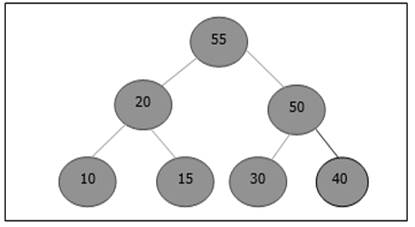
现在，我们必须停止。

示例

以下是此操作在各种编程语言中的实现：

C C++ Java Python

#include <stdio.h>
void swap(int* a, int* b) {
   int temp = *a;
   *a = *b;
   *b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(int arr[], int* heapSize, int key) {
   (*heapSize)++;
   int i = *heapSize;
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(&arr[i], &arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   int arr[100] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, &heapSize, newElement);
   // Print the updated Max-Heap
   printf("Updated Max-Heap: ");
   for (int i = 0; i <= heapSize; i++)
      printf("%d ", arr[i]);
   printf("\n");
   return 0;
}

输出

Updated Max-Heap: 50 30 40 20 15 10 5

#include <iostream>
#include <vector>
using namespace std;
void swap(int& a, int& b) {
   int temp = a;
   a = b;
   b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(vector<int>& arr, int& heapSize, int key) {
   heapSize++;
   int i = heapSize;   
   // Resize the vector to accommodate the new element
   arr.push_back(0);
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(arr[i], arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   vector<int> arr = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, heapSize, newElement);
   // Print the updated Max-Heap
   cout << "Updated Max-Heap: ";
   for (int i = 0; i <= heapSize; i++)
      cout << arr[i] << " ";
   cout << endl;
   return 0;
}

输出

Updated Max-Heap: 50 30 40 20 15 10 5

import java.util.Arrays;
public class MaxHeap {
   public static void swap(int arr[], int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
   }
   public static int parent(int i) {
      if (i == 0)
         return -1;
      else
         return (i - 1) / 2;
   }
   public static void maxHeapInsert(int arr[], int heapSize, int key) {
      heapSize++;
      int i = heapSize - 1; // Adjust the index for array insertion
      arr[i] = key;
      while (i > 0 && arr[parent(i)] < arr[i]) {
         swap(arr, i, parent(i));
         i = parent(i);
      }
   }
   public static void main(String args[]) {
      int arr[] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
      int heapSize = 5; // Current heap size
      // New element to be inserted
      int newElement = 5;
      // Insert the new element into the Max-Heap
      maxHeapInsert(arr, heapSize, newElement);
      // Print the updated Max-Heap
      System.out.print("Updated Max-Heap: ");
      for (int i = 0; i <= heapSize; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

输出

Updated Max-Heap: 50 30 40 20 15 5

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def parent(i):
    if i == 0:
        return -1
    else:
        return (i - 1) // 2
def max_heap_insert(arr, heap_size, key):
    heap_size += 1
    i = heap_size
    arr.append(key)
    while i > 0 and arr[parent(i)] < arr[i]:
        swap(arr, i, parent(i))
        i = parent(i)
if __name__ == "__main__":
    arr = [50, 30, 40, 20, 15, 10] # Initial Max-Heap
    heap_size = 5 # Current heap size
    # New element to be inserted
    new_element = 5
    # Insert the new element into the Max-Heap
    max_heap_insert(arr, heap_size, new_element)
    # Print the updated Max-Heap
    print("Updated Max-Heap:", arr)

输出

Updated Max-Heap: [50, 30, 40, 20, 15, 10, 5]

打印页面