数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究数学思维的发展
为了解决问题并理解数学概念，人们需要能够进行逻辑和分析性推理。这包括理解数字、公式、方程式和符号之间的关系，以及知道如何将这些关系应用于问题。为了发展数学思维，学生必须接触各种数学经验，并鼓励他们思考自己的思维和推理过程。
什么是数学思维的发展？
数学思维是一个推理过程，它涉及应用逻辑、抽象和解决问题的能力来解决数学问题。从简单的计算到尖端的科学和工程研究，它是一项基本技能，对于生活中许多方面的成功至关重要。通过互动游戏，幼儿可以培养他们的数学思维。例如，孩子们可以通过参与诸如玩棋盘游戏、对物体进行分类和解决谜题等活动来学习和理解基本的算术概念。随着孩子们年龄的增长，更具挑战性的活动，如绘图、几何和解决问题练习，将有助于他们数学思维能力的持续发展。
在初中和高中，可以通过更结构化的活动（包括单元计划、调查和模拟）来培养学生的数学思维能力。应鼓励学生在描述他们的推理和思维方式时使用数学术语。此外，他们应该有机会一起工作并与同伴交换想法。
随着学生在学术生涯中的进步，他们应该有机会利用他们的数学推理来解决现实世界的问题。他们将学习如何应用数学来解决日常生活中遇到的问题。最后，重要的是激励学生进行创造性思考并为解决问题制定原创的方法。
数学能力的组成部分
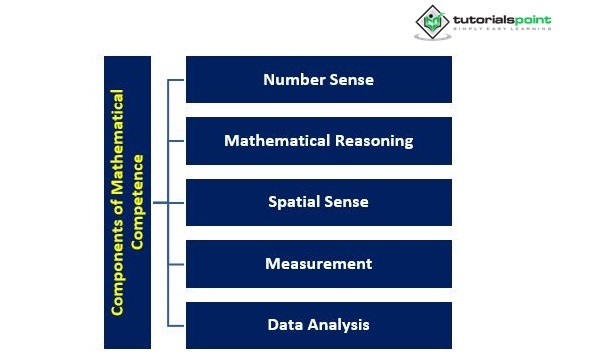
理解、使用和传达数学概念和推理的能力被称为数学能力。这是一个多维的概念，包括许多要素，例如 -
数感 - 理解数字的特性以及它们之间如何相互关联被称为数感。它包括能够进行加、减、乘、除的基本算术运算，以及理解数字的相对大小和位值。
数学推理 - 将逻辑、演绎和批判性思维应用于解决问题和理解数学概念被称为数学推理。它包括模式识别、假设生成和证明开发等能力。
空间感 - 空间感是理解和可视化空间关系和几何概念的能力。它包括识别形状及其属性、理解空间变换（如旋转和反射）以及可视化三维物体等技能。
测量 - 测量包括理解和使用计量单位、估计数量以及准确计算测量值的能力。它包括在计量单位之间进行转换、使用合适的工具测量物体以及理解计量单位之间关系等技能。
数据分析 - 数据分析包括使用统计方法收集、组织和解释数据的能力。它包括创建和解释图表、计算集中趋势和变异性指标以及根据数据进行预测等技能。
设计强大的数学学习环境
设计强大的数学学习环境需要仔细关注一系列可能影响学生参与度、学习和成就的因素。以下是一些关键考虑因素 -
创造积极和包容的学习环境 - 积极和包容的学习环境可以帮助学生感到安全和受到支持，这对他们的学习动机和参与至关重要。这可以通过诸如建立明确的行为期望、在课堂上培养社区意识以及为学生提供表达意见和选择的机会等策略来实现。
使用各种教学策略 - 有效的数学教学应包括一系列教学策略，例如直接教学、基于问题的学习和基于探究的学习。这可以帮助学生对数学概念和技能有深入的理解，并培养他们的解决问题和推理能力
融入技术 - 技术可以成为增强数学教学和吸引学生的强大工具。这可能包括使用交互式工具和模拟、将数字媒体融入教学以及为学生提供使用技术进行协作和交流的机会。
使用真实且相关的任务 - 为学生提供真实且相关的数学任务可以帮助他们了解数学的现实世界相关性，并增强他们的学习动机和参与度。这可能包括分析来自现实世界来源的数据、解决与社区问题相关的难题以及在学生兴趣和经验的背景下探索数学概念等任务。
提供协作和交流的机会 - 协作和交流是数学以及生活中许多其他领域的重要的技能。为学生提供小组合作、分享想法和解释推理的机会可以帮助他们培养这些技能并对数学概念有更深入的理解。
数学思维的评估
数学学习的评估是有效教学的关键组成部分。它为教师提供了有关学生优势和劣势的信息，并帮助他们确定学生可能需要额外支持或指导的领域。以下是在评估数学学习时的一些关键考虑因素 -
使用各种评估方法 - 数学学习的评估应包括一系列方法，例如形成性评估（例如，课堂观察、课堂小测验、测验）、总结性评估（例如，测试、项目、演示）和自我评估（例如，学生反思、同伴评估）。这可以更全面地了解学生的学习情况，并支持分层教学。
促进学生自我评估 - 鼓励学生反思自己的学习并评估自己的进步可以支持元认知技能的发展，并增强学生对学习的所有权。这可以通过自我反思日记、同伴反馈和学生主导的会议等策略来实现。
利用评估数据为教学提供信息 - 评估数据应用于为教学提供信息并支持分层教学。这可能包括根据学生的评估结果为学生提供额外的支持或挑战，以及利用评估数据调整教学和节奏以更好地满足学生的需要。
将评估与学习目标保持一致 - 评估应与数学课程的学习目标保持一致。这确保了评估正在衡量学生预期学习的内容，并为评估学生学习提供了一个清晰且一致的框架。
提供及时和具体的反馈 - 反馈是评估的重要方面，因为它可以帮助学生了解自己的优势和劣势，并为改进提供指导。反馈应及时、具体且可操作，并且应关注学习过程和学习成果。
个体差异
没有两个孩子是完全一样的。他们的学习速度不同，反应也不同，并且有着不同的生活经历。然而，研究揭示了所有这些差异中的一个模式。孩子们经历了认知发展的许多阶段。每个阶段都建立在之前的阶段之上。皮亚杰将这些认知发展阶段划分为感觉运动阶段、前运算阶段、具体运算阶段和形式运算阶段。
当孩子开始上小学时，她已经到达了具体运算阶段。此时，孩子可以通过实际的物质实验来理解抽象的数学概念。孩子在前运算阶段的判断完全取决于事物的表面现象。后来，孩子们到达了一个能够在感知层面上与数字建立联系的阶段。
皮亚杰讲述了一个五岁孩子玩石头收藏的故事。首先，他将它们排成一排并从左到右编号。一共有 10 个。然后他从左到右数了一遍。令他非常惊讶的是，数量再次是 10！他将它们排成一个圆圈，并顺时针和逆时针数了一遍。他发现无论他如何数，总是有 10 个石头。
上述情况超出了成年人的理解范围，但孩子们通过执行我们之前看到的操作说服了他们。孩子在具体运算阶段获得了守恒的概念，孩子在 6 到 10 岁之间经历这个阶段，也就是在小学阶段。认知发展的最后阶段发生在孩子 11 岁或以上的时候。只有现在，孩子才能获得使用形式运算并用文字或符号表示数量或事物的能力。孩子现在可以处理假设陈述并探索陈述之间的逻辑联系。
结论
有效的数学教育需要专注于培养数学能力、设计强大的学习环境以及使用多种评估方法。这需要创建包容性的课堂、使用各种教学策略、融入技术、提供真实的学习任务、支持合作和交流，以及使用评估数据来指导教学。通过关注这些因素，教师可以支持学生在数学方面的学习和成就。
63 次浏览
