
数字通信 - 增量调制
信号的采样率应高于奈奎斯特率,以实现更好的采样。如果差分脉冲编码调制中的此采样间隔大幅减小,则样本间的幅度差非常小,如果该差异为**1 位量化**,则步长将非常小,即**Δ**(delta)。
增量调制
采样率高且量化后步长值较小(**Δ**)的调制类型称为**增量调制**。
增量调制的特点
以下是增量调制的一些特点。
采用过采样输入以充分利用信号相关性。
量化设计简单。
输入序列远高于奈奎斯特率。
质量中等。
调制器和解调器的设计简单。
输出波形的阶梯近似。
步长非常小,即**Δ**(delta)。
用户可以决定比特率。
这涉及更简单的实现。
增量调制是差分脉冲编码调制技术的一种简化形式,也可视为**1 位差分脉冲编码调制方案**。随着采样间隔的减小,信号相关性将更高。
增量调制器
增量调制器包括一个 1 位量化器和一个延迟电路以及两个加法器电路。以下是增量调制器的框图。
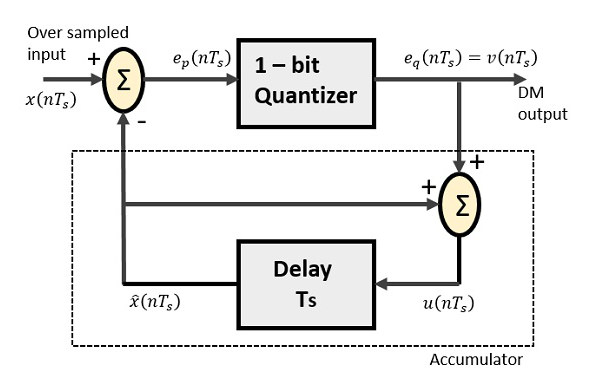
差分脉冲编码调制中的预测器电路在增量调制中被一个简单的延迟电路取代。
从上图,我们有以下符号 -
$x(nT_{s})$ = 过采样输入
$e_{p}(nT_{s})$ = 加法器输出和量化器输入
$e_{q}(nT_{s})$ = 量化器输出 = $v(nT_s)$
$\widehat{x}(nT_{s})$ = 延迟电路的输出
$u(nT_{s})$ = 延迟电路的输入
使用这些符号,我们现在将尝试弄清楚增量调制的过程。
$e_{p}(nT_{s}) = x(nT_{s}) - \widehat{x}(nT_{s})$
---------公式 1
$= x(nT_{s}) - u([n - 1]T_{s})$
$= x(nT_{s}) - [\widehat{x} [[n - 1]T_{s}] + v[[n-1]T_{s}]]$
---------公式 2
此外,
$v(nT_{s}) = e_{q}(nT_{s}) = S.sig.[e_{p}(nT_{s})]$
---------公式 3
$u(nT_{s}) = \widehat{x}(nT_{s})+e_{q}(nT_{s})$
其中,
$\widehat{x}(nT_{s})$ = 延迟电路的先前值
$e_{q}(nT_{s})$ = 量化器输出 = $v(nT_s)$
因此,
$u(nT_{s}) = u([n-1]T_{s}) + v(nT_{s})$
---------公式 4
这意味着,
延迟单元的当前输入
= (延迟单元的先前输出)+ (当前量化器输出)
假设累积的零条件,
$u(nT_{s}) = S \displaystyle\sum\limits_{j=1}^n sig[e_{p}(jT_{s})]$
**增量调制输出的累积版本** = $\displaystyle\sum\limits_{j = 1}^n v(jT_{s})$
---------公式 5
现在,请注意
$\widehat{x}(nT_{s}) = u([n-1]T_{s})$
$= \displaystyle\sum\limits_{j = 1}^{n - 1} v(jT_{s})$
---------公式 6
延迟单元输出是滞后一个样本的累加器输出。
根据公式 5 和 6,我们可以得到解调器的一种可能的结构。
阶梯近似波形将是增量调制器的输出,步长为 delta(**Δ**)。波形的输出质量中等。
增量解调器
增量解调器包括一个低通滤波器、一个加法器和一个延迟电路。此处消除了预测器电路,因此没有假设输入提供给解调器。
以下是增量解调器的图。
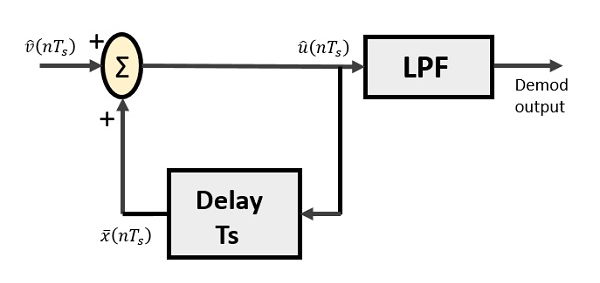
从上图,我们有以下符号 -
$\widehat{v}(nT_{s})$ 是输入样本
$\widehat{u}(nT_{s})$ 是加法器输出
$\bar{x}(nT_{s})$ 是延迟输出
二进制序列将作为输入提供给解调器。阶梯近似输出提供给低通滤波器。
使用低通滤波器的原因有很多,但主要原因是消除带外信号的噪声。发射机可能发生的步长误差称为**颗粒噪声**,此处将其消除。如果不存在噪声,则调制器输出等于解调器输入。
增量调制优于差分脉冲编码调制的优势
1 位量化器
调制器和解调器的设计非常简单
但是,增量调制中存在一些噪声。
斜率过载失真(当**Δ**较小时)
颗粒噪声(当**Δ**较大时)
自适应增量调制 (ADM)
在数字调制中,我们遇到了一些确定步长的问题,步长会影响输出波形的质量。
在调制信号的陡峭斜率处需要较大的步长,而在消息斜率较小的地方需要较小的步长。在此过程中,细微的细节会被遗漏。因此,如果我们可以根据我们的要求控制步长的调整,以便以所需的方式获得采样,将会更好。这就是**自适应增量调制**的概念。
以下是自适应增量调制器的框图。
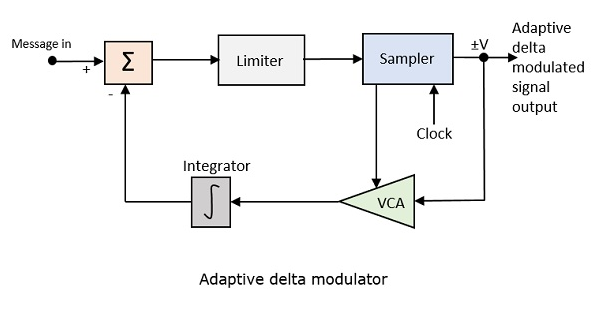
电压控制放大器的增益由采样器的输出信号调整。放大器增益决定步长,两者成正比。
ADM 量化当前样本值与下一个样本的预测值之间的差值。它使用可变步高来预测下一个值,以忠实地再现快速变化的值。