
数字通信 - 采样
采样定义为:“以离散形式测量连续时间信号瞬时值的过程。”
样本是从整体数据中提取的一段数据,在时域上是连续的。
当信源产生模拟信号,并且该信号需要被数字化,即具有1和0(高或低)时,该信号必须在时间上离散化。这种模拟信号的离散化称为采样。
下图显示了连续时间信号x(t)和采样信号xs(t)。当x(t)与周期性脉冲序列相乘时,得到采样信号xs(t)。
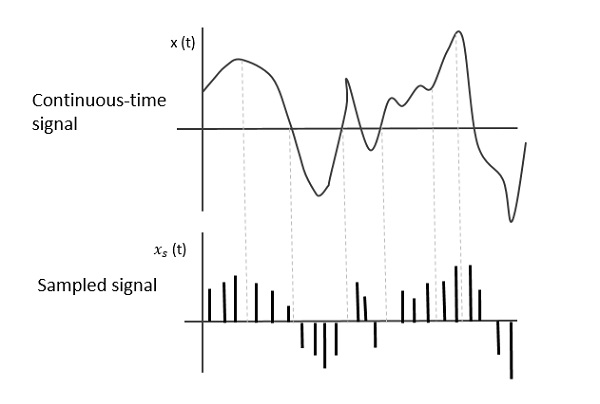
采样率
为了使信号离散化,样本之间的间隔应该固定。该间隔可以称为采样周期Ts。
$$采样频率 = \frac{1}{T_{s}} = f_s$$其中:
$T_{s}$为采样时间
$f_{s}$为采样频率或采样率
采样频率是采样周期的倒数。这个采样频率可以简单地称为采样率。采样率表示每秒采集的样本数,或有限值集的样本数。
为了从数字化信号重建模拟信号,必须高度重视采样率。采样率应使得消息信号中的数据既不会丢失也不会重叠。因此,为此确定了一个速率,称为奈奎斯特率。
奈奎斯特率
假设一个信号是带限的,没有高于W赫兹的频率分量。这意味着W是最高频率。对于这样的信号,为了有效地再现原始信号,采样率应为最高频率的两倍。
这意味着:
$$f_{S} = 2W$$其中:
$f_{S}$是采样率
W是最高频率
这种采样率称为奈奎斯特率。
一个称为采样定理的定理是基于这个奈奎斯特率的理论。
采样定理
采样定理,也称为奈奎斯特定理,根据带限函数类的带宽,提供了关于足够采样率的理论。
采样定理指出:“如果以大于最大频率W两倍的速率fs对信号进行采样,则可以精确地再现该信号。”
为了理解这个采样定理,让我们考虑一个带限信号,即其值在某个–W和W赫兹之间非零的信号。
这样的信号表示为$x(f) = 0 对于 |f| > W$
对于连续时间信号x(t),频域中的带限信号可以如下图所示。
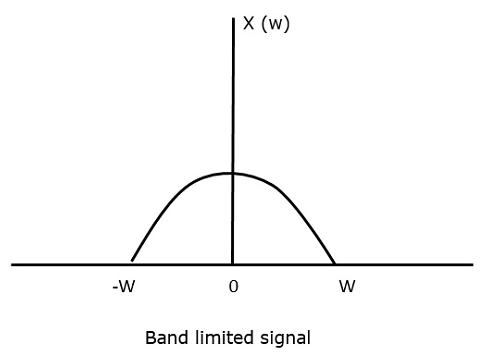
我们需要一个采样频率,在这个频率下,即使在采样后也不会有信息丢失。为此,我们有奈奎斯特率,即采样频率应为最大频率的两倍。这是临界的采样率。
如果信号x(t)的采样率高于奈奎斯特率,则可以恢复原始信号;如果采样率低于奈奎斯特率,则无法恢复信号。
下图解释了在频域中以高于2w的速率采样的信号。
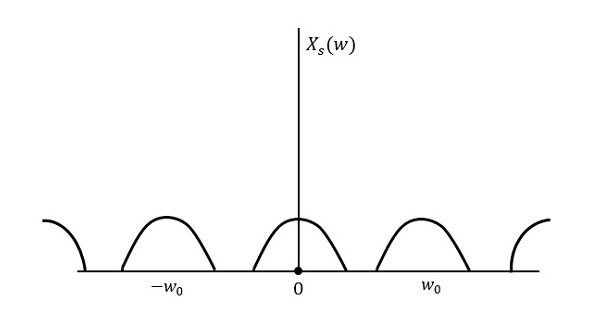
上图显示了信号$x_{s}(t)$的傅里叶变换。在这里,信息在没有任何损失的情况下被再现。没有混合,因此可以恢复。
信号$x_{s}(t)$的傅里叶变换是
$$X_{s}(w) = \frac{1}{T_{s}}\sum_{n = - \infty}^\infty X(w-nw_0)$$其中$T_{s}$ = 采样周期,$w_{0} = \frac{2 \pi}{T_s}$
让我们看看如果采样率等于最高频率的两倍(2W)会发生什么
这意味着:
$$f_{s} = 2W$$其中:
$f_{s}$是采样频率
W是最高频率
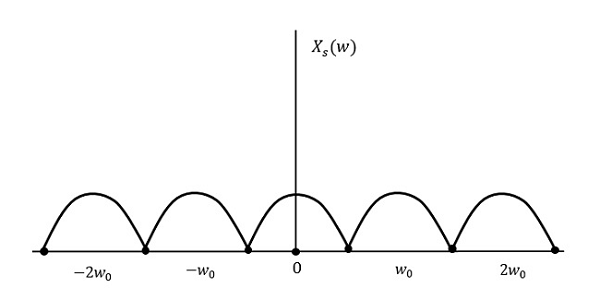
结果将如上图所示。信息在没有任何损失的情况下被替换。因此,这也是一个良好的采样率。
现在,让我们来看一下这个条件:
$$f_{s} < 2W$$所得图案将如下图所示。
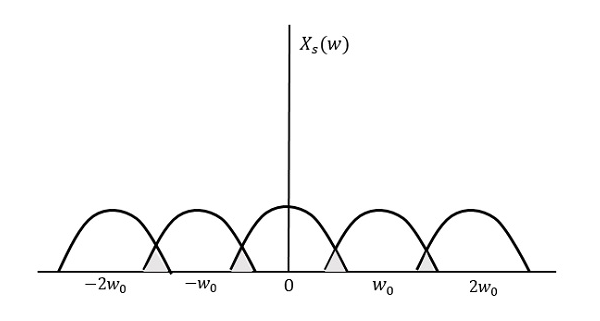
从上图可以看出,信息发生了重叠,导致信息混合和丢失。这种不希望出现的重叠现象称为混叠。
混叠
混叠可以指“信号频谱中的高频分量在其采样版本的频谱中呈现为低频分量的现象”。
为减少混叠效应而采取的纠正措施包括:
在PCM的发射机部分,在采样器之前采用低通抗混叠滤波器,以消除不需要的高频分量。
经过滤波后采样的信号以略高于奈奎斯特率的速率进行采样。
选择高于奈奎斯特率的采样率也有助于更容易设计接收端的重建滤波器。
傅里叶变换的范围
通常观察到,我们在分析信号和证明定理时会借助傅里叶级数和傅里叶变换。这是因为:
傅里叶变换是非周期信号的傅里叶级数的扩展。
傅里叶变换是一种强大的数学工具,它有助于在不同的域中查看信号,并有助于轻松地分析信号。
使用傅里叶变换,任何信号都可以分解为正弦和余弦的总和。
在下一章中,我们将讨论量化的概念。