数字通信 - 快速指南

数字通信 - 模拟到数字

我们日常生活中发生的通信是以信号的形式出现的。这些信号，例如声音信号，通常是模拟性质的。当需要建立远距离通信时，模拟信号通过导线传输，使用不同的技术来实现有效的传输。

数字化的必要性

传统的通信方法使用模拟信号进行长距离通信，但存在许多损耗，例如失真、干扰和其他损耗，包括安全漏洞。

为了克服这些问题，使用不同的技术对信号进行数字化。数字化信号允许通信更加清晰和准确，而不会出现损耗。

下图显示了模拟信号和数字信号之间的区别。数字信号由**1**和**0**组成，分别表示高值和低值。

数字通信的优势

由于信号已数字化，因此数字通信比模拟通信具有许多优势，例如：

数字信号受失真、噪声和干扰的影响较小。
数字电路更可靠。
数字电路的设计更容易，成本也比模拟电路低。
数字电路的硬件实现比模拟电路更灵活。
数字通信中串扰的发生非常罕见。
由于脉冲需要很大的干扰才能改变其特性，这非常困难，因此信号不会被改变。
数字电路中采用加密和压缩等信号处理功能来维护信息的机密性。
通过采用检错码和纠错码来降低错误发生的概率。
使用扩频技术来避免信号干扰。
使用时分多路复用 (TDM) 组合数字信号比使用频分多路复用 (FDM) 组合模拟信号更容易。
数字信号的配置过程比模拟信号更容易。
数字信号比模拟信号更方便保存和检索。
许多数字电路具有几乎相同的编码技术，因此类似的设备可以用于多种用途。
数字信号有效地利用了信道的容量。

数字通信的组成部分

为了便于理解，下图所示的框图表示构成数字通信系统的组成部分。

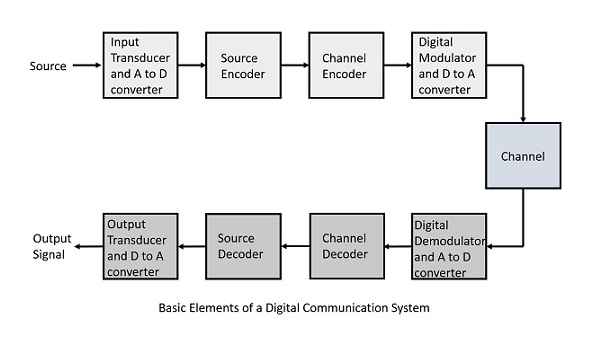
以下是数字通信系统的各个部分。

信源

信源可以是**模拟**信号。**例如**: 声音信号

这是一个传感器，它接收物理输入并将其转换为电信号 (例如: 麦克风)。此模块还包含一个模拟到数字转换器，在需要数字信号进行进一步处理的情况下。

输入传感器

数字信号通常由二进制序列表示。

信源编码器

信源编码器将数据压缩到最少的位数。此过程有助于有效利用带宽。它去除冗余位（不必要的额外位，即零）。

信道编码器

信道编码器进行纠错编码。在信号传输过程中，由于信道中的噪声，信号可能会发生改变，因此为了避免这种情况，信道编码器会向传输的数据添加一些冗余位。这些是纠错位。

数字调制器

此处将要传输的信号由载波调制。为了使其能够通过信道或介质传输，信号也从数字序列转换为模拟信号。

信道

信道或介质允许模拟信号从发射端传输到接收端。

数字解调器

这是接收端的第一个步骤。接收到的信号被解调并再次从模拟转换为数字。信号在此处被重建。

信道解码器

信道解码器在检测到序列后，进行一些纠错。传输过程中可能发生的失真通过添加一些冗余位来纠正。添加这些位有助于完全恢复原始信号。

信源解码器

通过采样和量化再次对所得信号进行数字化，以便获得纯数字输出，而不会丢失信息。信源解码器重建信源输出。

输出传感器

这是最后一个模块，它将信号转换为原始物理形式，该形式在发射机的输入端。

它将电信号转换为物理输出(**例如**: 扬声器)。

输出信号

这是整个过程结束后产生的输出。**例如**- 收到的声音信号。

本单元介绍了数字通信的介绍、信号数字化、优势和组成部分。在接下来的章节中，我们将详细学习数字通信的概念。

脉冲编码调制

**调制**是根据消息信号的瞬时值改变载波信号的一个或多个参数的过程。

消息信号是要传输的通信信号，载波信号是高频信号，没有数据，但用于长距离传输。

有许多调制技术，根据所采用的调制类型进行分类。其中，使用的数字调制技术是**脉冲编码调制 (PCM)**。

对信号进行脉冲编码调制以将其模拟信息转换为二进制序列，即**1**和**0**。PCM 的输出将类似于二进制序列。下图显示了关于给定正弦波的瞬时值的 PCM 输出示例。

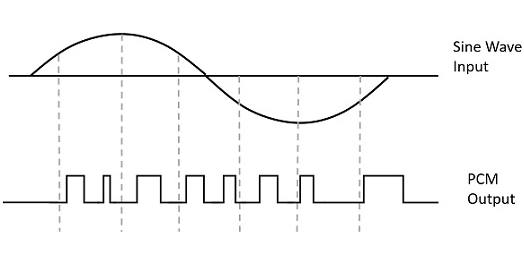
PCM 产生一系列数字而不是脉冲序列，因此此过程称为**数字**。每个数字虽然采用二进制代码，但表示该时刻信号样本的近似幅度。

在脉冲编码调制中，消息信号由一系列编码脉冲表示。通过在时间和幅度上以离散形式表示信号来实现此消息信号。

PCM 的基本元件

脉冲编码调制电路的发射机部分包括**采样、量化**和**编码**，这些操作在模拟到数字转换器部分执行。采样之前的低通滤波器可防止消息信号混叠。

接收机部分的基本操作是**受损信号的再生、解码**和量化脉冲序列的**重建**。以下是 PCM 的框图，它表示发射机和接收机部分的基本元件。

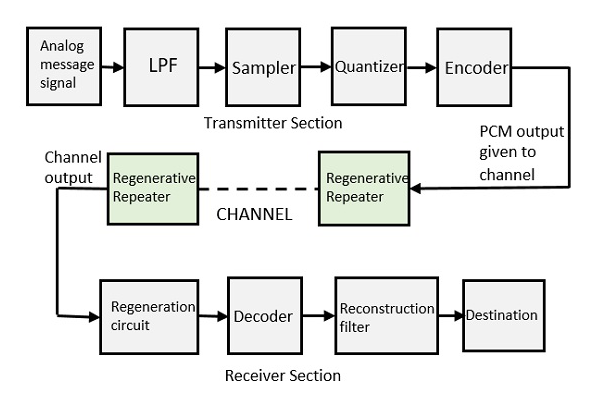
低通滤波器

此滤波器消除输入模拟信号中存在的高于消息信号最高频率的高频分量，以避免消息信号混叠。

采样器

这是一种技术，它有助于在消息信号的瞬时值处收集样本数据，以便重建原始信号。根据采样定理，采样率必须大于消息信号最高频率分量**W**的两倍。

量化器

量化是减少多余位和限制数据的过程。当对量化器提供采样输出时，它会减少冗余位并压缩值。

编码器

编码器对模拟信号进行数字化。它用二进制代码指定每个量化级别。此处进行的采样是采样保持过程。这三个部分（低通滤波器、采样器和量化器）将充当模拟到数字转换器。编码最小化了使用的带宽。

再生中继器

此部分提高信号强度。信道的输出也具有一个再生中继器电路，以补偿信号损耗并重建信号，以及提高其强度。

解码器

解码器电路对脉冲编码波形进行解码以重现原始信号。该电路充当解调器。

重建滤波器

在再生电路和解码器完成数字到模拟转换后，采用低通滤波器（称为重建滤波器）来恢复原始信号。

因此，脉冲编码调制电路对给定的模拟信号进行数字化、编码和采样，然后以模拟形式传输。重复整个过程的反向模式以获得原始信号。

数字通信 - 采样

**采样**定义为“以离散形式测量连续时间信号瞬时值的过程”。

**样本**是从时域连续的整个数据中提取的一段数据。

当信源产生模拟信号并且该信号必须数字化，具有**1**和**0**，即高或低时，必须在时间上对信号进行离散化。这种模拟信号的离散化称为采样。

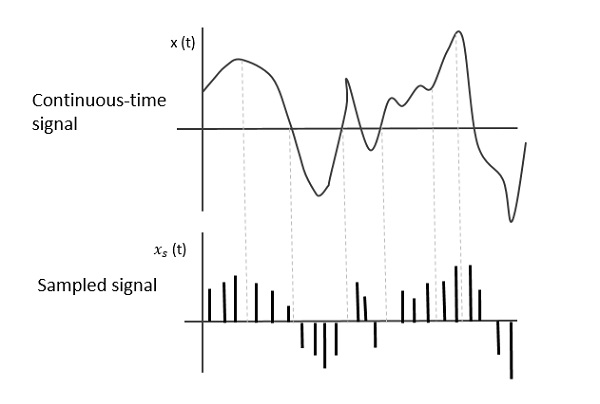
下图显示了连续时间信号**x(t)**和采样信号**x_s(t)**。当**x(t)**乘以周期性脉冲序列时，便获得采样信号**x_s(t)**。

采样率

为了对信号进行离散化，样本之间的间隙应固定。该间隙可以称为**采样周期T_s**。

$$采样频率 = \frac{1}{T_{s}} = f_s$$

其中，

T_s是采样时间
f_s是采样频率或采样率

**采样频率**是采样周期的倒数。此采样频率可以简称为**采样率**。采样率表示每秒采集的样本数，或一组有限的值。

为了从数字化信号重建模拟信号，必须高度重视采样率。采样率应使得消息信号中的数据既不会丢失，也不会重叠。因此，为此确定了一个速率，称为奈奎斯特率。

奈奎斯特率

假设信号是带限的，没有高于**W**赫兹的频率分量。这意味着**W**是最高频率。对于这样的信号，为了有效地再现原始信号，采样率应为最高频率的两倍。

这意味着，

$$f_S = 2W$$

其中，

$f_S$ 是采样率
W 是最高频率

这种采样率被称为奈奎斯特率。

关于奈奎斯特率的理论，有一个定理叫做采样定理。

采样定理

采样定理，也称为奈奎斯特定理，为带限函数类提供了关于带宽方面足够采样率的理论。

采样定理指出：“如果以大于最大频率W两倍的速率f_s对信号进行采样，则可以精确地重构该信号。”

为了理解这个采样定理，让我们考虑一个带限信号，即在某个–W和W赫兹之间值非零的信号。

这样的信号表示为 $x(f) = 0 \: for \: \mid f \mid > W$

对于连续时间信号x (t)，频域中的带限信号可以如下图所示。

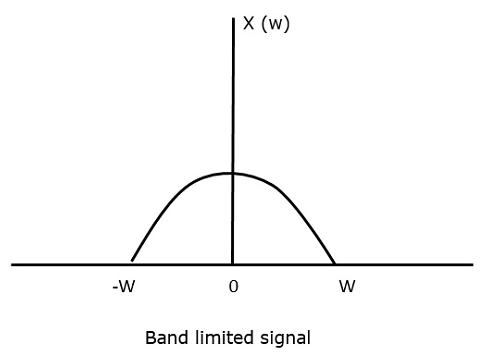
我们需要一个采样频率，在这个频率下，即使在采样后也不会有信息丢失。为此，我们有奈奎斯特率，即采样频率应为最大频率的两倍。这是临界采样率。

如果信号x(t)的采样率高于奈奎斯特率，则可以恢复原始信号；如果采样率低于奈奎斯特率，则无法恢复信号。

下图说明了如果在频域中以高于2w的速率对信号进行采样。

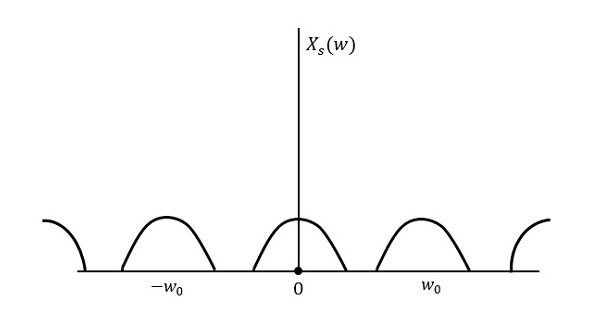
上图显示了信号x_s (t)的傅里叶变换。在这里，信息在没有任何损失的情况下被重现。没有混叠，因此可以恢复。

信号x_s (t)的傅里叶变换为

$$X_s(w) = \frac{1}{T_{s}}\sum_{n = - \infty}^\infty X(w-nw_0)$$

其中 $T_s$ = 采样周期 和 $w_0 = \frac{2 \pi}{T_s}$

让我们看看如果采样率等于最高频率的两倍 (2W) 会发生什么

这意味着：

$$f_s = 2W$$

其中，

$f_s$ 是采样频率
W 是最高频率

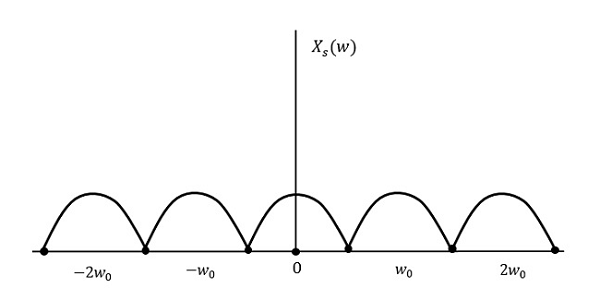
结果将如上图所示。信息被无损地复制。因此，这也是一个良好的采样率。

现在，让我们来看一下这个条件：

$$f_s < 2W$$

结果模式将如下图所示。

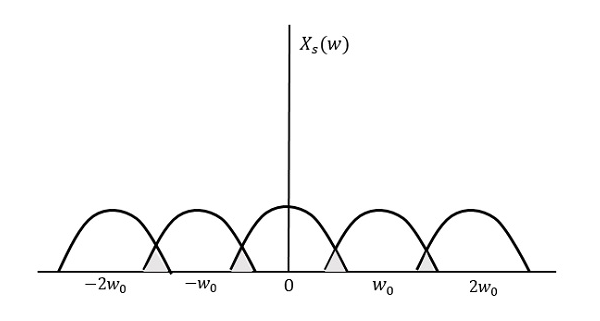
从上图可以看出，信息发生了重叠，导致信息混合和丢失。这种不需要的重叠现象称为混叠。

混叠

混叠可以指“信号频谱中的高频分量在其采样版本的频谱中呈现为低频分量的现象。”

为减少混叠效应而采取的纠正措施：

在PCM的发射机部分，在采样器之前使用低通抗混叠滤波器来消除不需要的高频分量。
滤波后采样的信号以略高于奈奎斯特率的速率进行采样。

选择高于奈奎斯特率的采样率也有助于更容易地设计接收机中的重建滤波器。

傅里叶变换的范围

通常观察到，我们在分析信号和证明定理时会寻求傅里叶级数和傅里叶变换的帮助。这是因为：

傅里叶变换是非周期信号的傅里叶级数的扩展。
傅里叶变换是一种强大的数学工具，它有助于在不同的域中查看信号，并有助于轻松分析信号。
使用傅里叶变换，任何信号都可以分解为正弦和余弦之和。

在下一章中，让我们讨论量化的概念。

数字通信 - 量化

模拟信号的数字化涉及对近似等于模拟值的数值进行四舍五入。采样方法选择模拟信号上的几个点，然后将这些点连接起来，将值四舍五入到接近稳定的值。这样的过程称为量化。

模拟信号的量化

模数转换器执行这种类型的功能，以根据给定的模拟信号创建一系列数字值。下图表示一个模拟信号。为了将此信号转换为数字信号，必须对其进行采样和量化。

模拟信号的量化是通过用许多量化级别对信号进行离散化来完成的。量化是用有限的电平表示样本幅度的采样值，这意味着将连续幅度的样本转换为离散时间信号。

下图显示了模拟信号如何进行量化。蓝线表示模拟信号，棕色线表示量化信号。

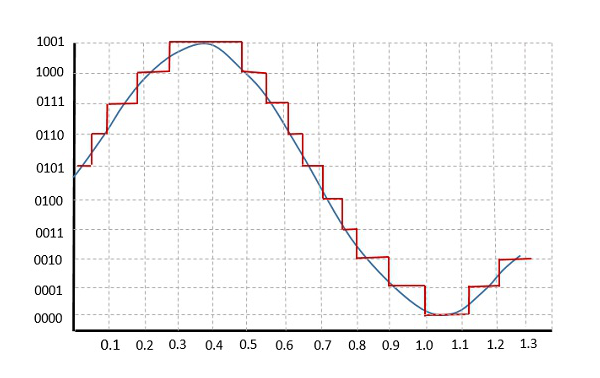
采样和量化都会导致信息丢失。量化器输出的质量取决于使用的量化级别数。量化输出的离散幅度称为表示级别或重建级别。两个相邻表示级别之间的间距称为量子或步长。

下图显示了所得的量化信号，它是给定模拟信号的数字形式。

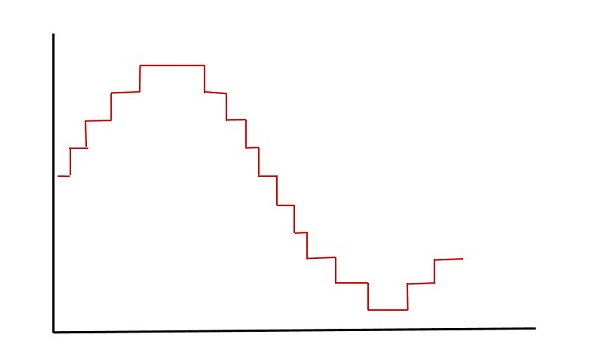
根据其形状，这也称为阶梯波形。

量化类型

量化有两种类型：均匀量化和非均匀量化。

量化级别均匀分布的量化类型称为均匀量化。量化级别不相等且它们之间的关系大多是对数关系的量化类型称为非均匀量化。

均匀量化有两种类型。它们是中位上升型和中位踏步型。下图表示两种类型的均匀量化。

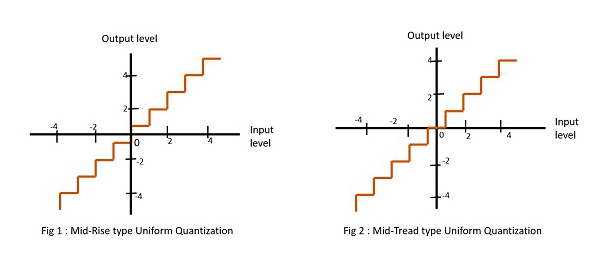
图1显示了中位上升型，图2显示了中位踏步型均匀量化。

中位上升型之所以这样命名，是因为原点位于阶梯状图表的上升部分的中间。这种类型的量化级别是偶数。
中位踏步型之所以这样命名，是因为原点位于阶梯状图表的踏步中间。这种类型的量化级别是奇数。
中位上升型和中位踏步型均匀量化器都关于原点对称。

量化误差

对于任何系统，在其运行过程中，其输入值和输出值之间总存在差异。系统的处理会导致误差，这是这些值的差值。

输入值与其量化值之间的差异称为量化误差。量化器是一个执行量化（对值进行四舍五入）的对数函数。模数转换器 (ADC) 充当量化器。

下图说明了量化误差的一个例子，指出了原始信号和量化信号之间的差异。

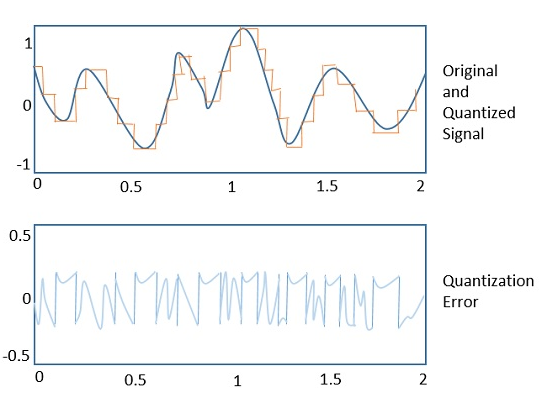
量化噪声

这是一种量化误差，通常发生在模拟音频信号中，在将其量化为数字信号时。例如，在音乐中，信号持续不断地变化，而误差中没有规律性。这些误差会产生称为量化噪声的宽带噪声。

PCM中的压扩

压扩这个词是压缩和扩展的组合，这意味着它两者都做。这是一种在PCM中使用的非线性技术，它在发射机端压缩数据，在接收机端扩展相同的数据。使用这种技术可以降低噪声和串扰的影响。

压扩技术有两种类型：

A律压扩技术

在A = 1时实现均匀量化，其中特性曲线是线性的，并且没有进行压缩。
A律在原点处具有中位上升。因此，它包含非零值。
A律压扩用于PCM电话系统。

μ律压扩技术

在μ = 0时实现均匀量化，其中特性曲线是线性的，并且没有进行压缩。
μ律在原点处具有中位踏步。因此，它包含零值。
μ律压扩用于语音和音乐信号。

μ律在美国和日本使用。

数字通信 - 差分脉冲编码调制 (DPCM)

对于高度相关的样本，当使用PCM技术进行编码时，会留下冗余信息。为了处理这些冗余信息并获得更好的输出，明智的做法是从其之前的输出中假设一个预测的采样值，并将它们与量化值汇总。这样的过程称为差分脉冲编码调制 (DPCM)技术。

DPCM发射机

DPCM发射机由量化器和预测器以及两个加法器电路组成。以下是DPCM发射机的框图。

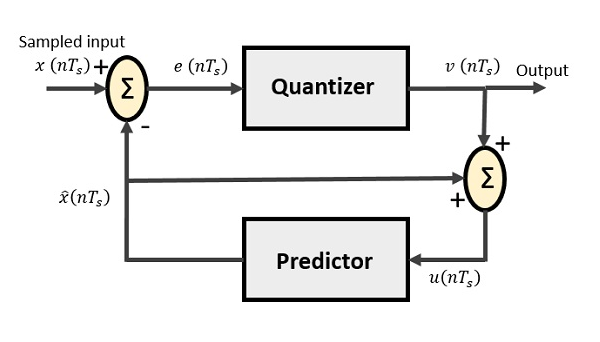
每个点的信号命名为：

$x(nT_s)$ 是采样输入
$\widehat{x}(nT_s)$ 是预测样本
$e(nT_s)$ 是采样输入和预测输出的差值，通常称为预测误差
$v(nT_s)$ 是量化输出
$u(nT_s)$ 是预测器输入，实际上是预测器输出和量化器输出的加法器输出

预测器根据发射机电路的先前输出产生假设样本。此预测器的输入是输入信号 $x(nT_s)$ 的量化版本。

量化器输出表示为：

$$v(nT_s) = Q[e(nT_s)]$$

$= e(nT_s) + q(nT_s)$

其中q (nT_s)是量化误差

预测器输入是量化器输出和预测器输出的总和，

$$u(nT_s) = \widehat{x}(nT_s) + v(nT_s)$$

$u(nT_s) = \widehat{x}(nT_s) + e(nT_s) + q(nT_s)$

$$u(nT_s) = x(nT_s) + q(nT_s)$$

解码器中使用相同的预测器电路来重建原始输入。

DPCM接收机

DPCM接收机的框图由解码器、预测器和加法器电路组成。以下是DPCM接收机的图。

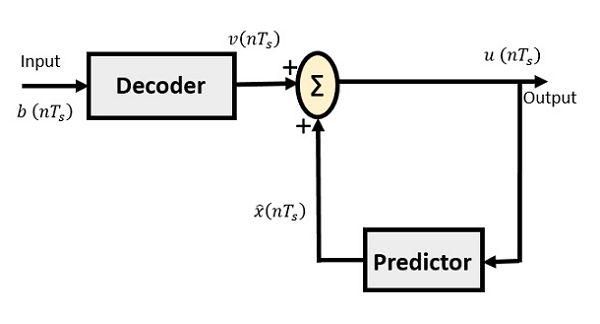
信号的表示法与之前的相同。在没有噪声的情况下，编码的接收机输入将与编码的发射机输出相同。

如前所述，预测器根据先前的输出假设一个值。给解码器的输入进行处理，并将该输出与预测器的输出相加，以获得更好的输出。

数字通信 - 增量调制

为了获得更好的采样，信号的采样率应该高于奈奎斯特率。如果差分脉冲编码调制中的采样间隔大大减少，则样本间的幅度差将非常小，如果差值为1比特量化，则步长将非常小，即Δ（增量）。

增量调制

采样率高得多，并且量化后的步长值较小Δ的调制类型，这种调制称为增量调制。

增量调制的特点

以下是增量调制的一些特点。

采用过采样输入以充分利用信号相关性。
量化设计简单。
输入序列远高于奈奎斯特率。
质量中等。
调制器和解调器的设计简单。
输出波形的阶梯式逼近。
步长非常小，即Δ（增量）。
比特率可由用户决定。
这涉及更简单的实现。

增量调制是DPCM技术的简化形式，也可视为1比特DPCM方案。随着采样间隔的减小，信号相关性将更高。

增量调制器

增量调制器由一个1比特量化器、一个延时电路和两个加法器组成。以下是增量调制器的框图。

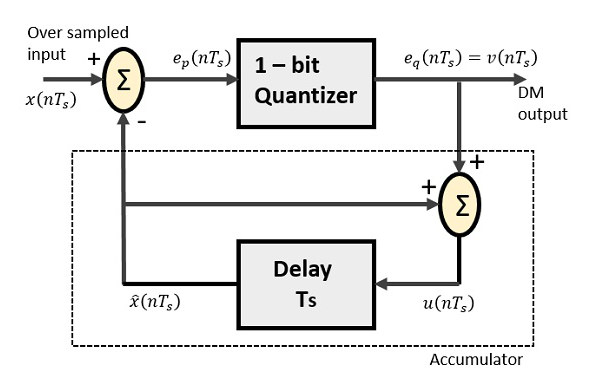
在差分脉冲编码调制(DPCM)中的预测电路在增量调制(DM)中被一个简单的延时电路代替。

从上图中，我们有以下符号：

$x(nT_s)$ = 过采样输入
$e_p(nT_s)$ = 加法器输出和量化器输入
$e_q(nT_s)$ = 量化器输出 = $v(nT_s)$
$\widehat{x}(nT_s)$ = 延时电路输出
$u(nT_s)$ = 延时电路输入

使用这些符号，我们现在将尝试弄清楚增量调制的过程。

$e_p(nT_s) = x(nT_s) - \widehat{x}(nT_s)$

---------公式1

$= x(nT_s) - u([n - 1]T_s)$

$= x(nT_s) - [\widehat{x} [[n - 1]T_s] + v[[n-1]T_s]]$

---------公式2

此外，

$v(nT_s) = e_q(nT_s) = S.sig.[e_p(nT_s)]$

---------公式3

$u(nT_s) = \widehat{x}(nT_s)+e_q(nT_s)$

其中，

$\widehat{x}(nT_s)$ = 延时电路的先前值
$e_q(nT_s)$ = 量化器输出 = $v(nT_s)$

因此，

$u(nT_s) = u([n-1]T_s) + v(nT_s)$

---------公式4

这意味着，

延时单元的当前输入

= (延时单元的前一个输出) + (当前量化器输出)

假设累积为零，

$u(nT_s) = S \displaystyle\sum\limits_{j=1}^n sig[e_p(jT_s)]$

**DM输出的累积版本** = $\displaystyle\sum\limits_{j = 1}^n v(jT_s)$

---------公式5

现在，请注意

$\widehat{x}(nT_s) = u([n-1]T_s)$

$= \displaystyle\sum\limits_{j = 1}^{n - 1} v(jT_s)$

---------公式6

延时单元输出是滞后一个样本的累加器输出。

从公式5和6，我们可以得到解调器的可能结构。

阶梯逼近波形将是增量调制器的输出，步长为delta (**Δ**)。波形的输出质量中等。

增量解调器

增量解调器由一个低通滤波器、一个加法器和一个延时电路组成。这里的预测电路被消除，因此没有假设输入给出到解调器。

以下是增量解调器的图。

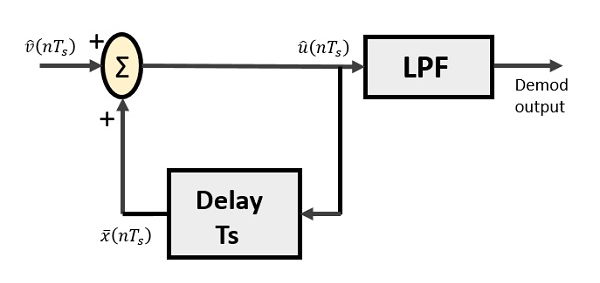
从上图中，我们有以下符号：

$\widehat{v}(nT_s)$ 是输入样本
$\widehat{u}(nT_s)$ 是加法器输出
$\bar{x}(nT_s)$ 是延迟输出

二进制序列将作为输入提供给解调器。阶梯逼近输出提供给低通滤波器。

使用低通滤波器的原因有很多，但最主要的原因是消除带外信号的噪声。在发射机可能出现的步长误差称为**颗粒噪声**，在这里被消除。如果没有噪声，则调制器输出等于解调器输入。

增量调制优于差分脉冲编码调制的优点

1比特量化器
调制器和解调器的设计非常简单

然而，增量调制中存在一些噪声。

斜率过载失真（当**Δ**很小时）
颗粒噪声（当**Δ**很大时）

自适应增量调制 (ADM)

在数字调制中，我们遇到了一些确定步长的问题，这会影响输出波的质量。

在调制信号的陡峭斜率处需要更大的步长，而在消息斜率较小的地方需要更小的步长。在这个过程中，细微的细节会被遗漏。因此，如果我们可以根据我们的要求控制步长的调整，以便以我们想要的方式获得采样，将会更好。这就是**自适应增量调制**的概念。

以下是自适应增量调制器的框图。

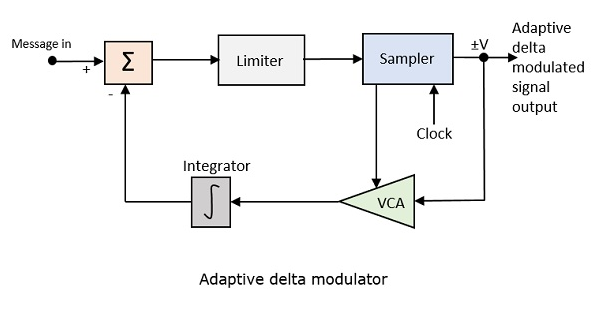
电压控制放大器的增益由采样器的输出信号调整。放大器增益决定步长，两者成正比。

ADM 量化当前样本值与下一个样本预测值之间的差值。它使用可变步高来预测下一个值，以忠实地再现快速变化的值。

数字通信 - 技术

有一些技术为数字通信过程奠定了基础。为了使信号数字化，我们有采样和量化技术。

为了用数学方法表示它们，我们有线性预测编码和数字多路复用技术。这些数字调制技术将在后面进一步讨论。

线性预测编码

**线性预测编码 (LPC)** 是一种使用线性预测模型表示数字语音信号的工具。这主要用于音频信号处理、语音合成、语音识别等。

线性预测基于这样的思想：当前样本基于过去样本的线性组合。该分析将离散时间信号的值估计为先前样本的线性函数。

使用线性预测模型的信息，以压缩形式表示频谱包络。这可以用数学方式表示为：

$s(n) = \displaystyle\sum\limits_{k = 1}^p \alpha_k s(n - k)$ 对于某个值 **p** 和 **α_k**

其中

**s(n)** 是当前语音样本
**k** 是特定样本
**p** 是最新的值
**α_k** 是预测系数
**s(n - k)** 是先前的语音样本

对于 LPC，通过最小化实际语音样本与线性预测样本之间平方差的总和（在一个有限的区间内）来确定预测系数的值。

这是一种非常有用的以低比特率**编码语音**的方法。LPC 方法非常接近**快速傅里叶变换 (FFT)** 方法。

多路复用

**多路复用**是将多个信号组合成一个信号，通过共享介质的过程。如果这些信号本质上是模拟信号，则该过程称为**模拟多路复用**。如果对数字信号进行多路复用，则称为**数字多路复用**。

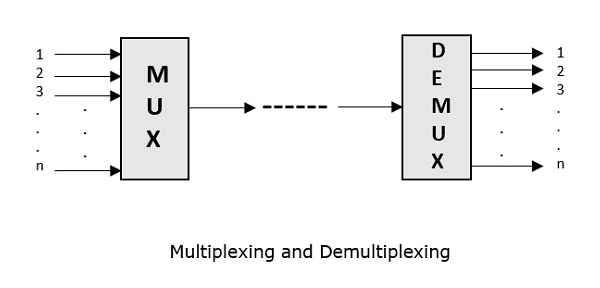
多路复用最初是在电话中开发的。许多信号被组合起来通过一根电缆发送。多路复用的过程将通信信道划分为多个逻辑信道，为每个逻辑信道分配不同的消息信号或要传输的数据流。执行多路复用的设备称为**MUX**。相反的过程，即从一个信号中提取多个信道，这在接收端完成，称为**解多路复用**。执行解多路复用的设备称为**DEMUX**。

下图显示了 MUX 和 DEMUX。它们主要用于通信领域。

多路复用器的类型

多路复用器主要有两种类型，即模拟和数字。它们进一步分为FDM、WDM和TDM。下图详细说明了这种分类。

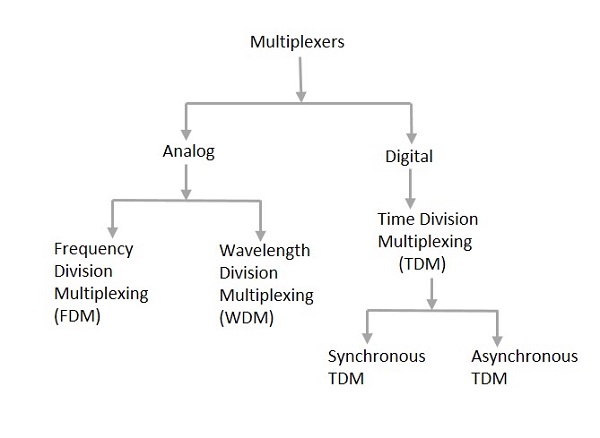
实际上，有多种多路复用技术。在所有这些技术中，我们有上面图中提到的主要类型和一般分类。

模拟多路复用

模拟多路复用技术涉及本质上是模拟的信号。模拟信号根据它们的频率 (FDM) 或波长 (WDM) 进行多路复用。

频分多路复用 (FDM)

在模拟多路复用中，最常用的技术是**频分多路复用 (FDM)**。这项技术使用不同的频率来组合数据流，以便将它们作为单个信号发送到通信介质上。

**示例** - 通过单根电缆发送多个频道的传统电视发射机使用 FDM。

波分多路复用 (WDM)

波分多路复用是一种模拟技术，其中许多不同波长的数据流在光谱中传输。如果波长增加，则信号频率降低。可以在 MUX 的输出和 DEMUX 的输入处使用可以将不同波长转换为单线的**棱镜**。

**示例** - 光纤通信使用 WDM 技术将不同波长合并成单束光进行通信。

数字多路复用

术语“数字”代表离散的信息位。因此，可用数据以帧或数据包的形式存在，这些帧或数据包是离散的。

时分多路复用 (TDM)

在 TDM 中，时间帧被分成时隙。这项技术用于通过分配给每个消息一个时隙，在单个通信信道上传输信号。

在所有类型的 TDM 中，主要类型是同步和异步 TDM。

同步 TDM

在同步 TDM 中，输入连接到一个帧。如果有“**n**”个连接，则该帧被分成“**n**”个时隙。为每个输入线路分配一个时隙。

在这种技术中，所有信号的采样率都是相同的，因此给出相同的时钟输入。MUX 始终为每个设备分配相同的时隙。

异步 TDM

在异步 TDM 中，每个信号的采样率不同，不需要公共时钟。如果为时隙分配的设备不传输任何内容并处于空闲状态，则该时隙将分配给另一个设备，这与同步不同。这种类型的 TDM 用于异步传输模式网络。

再生中继器

对于任何可靠的通信系统，它都应该有效地传输和接收信号，而不会有任何损失。PCM 波在通过信道传输后，由于信道引入的噪声而发生失真。

再生脉冲与原始脉冲和接收脉冲的比较，如下图所示。

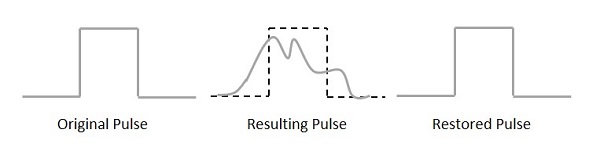
为了更好地再现信号，在接收器之前的路径中采用了一个称为**再生中继器**的电路。这有助于恢复因损失而造成的信号。

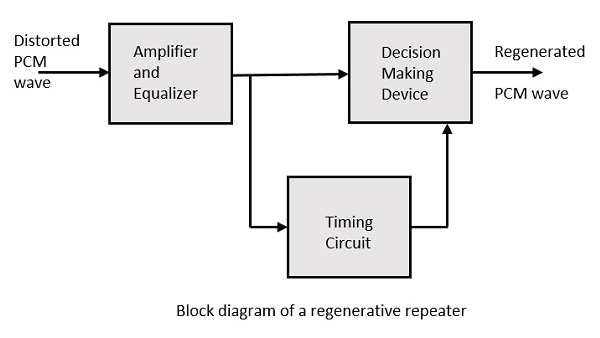
这包括一个均衡器以及一个放大器、一个定时电路和一个决策设备。每个组件的工作原理如下所示。

均衡器

信道会对信号产生幅度和相位失真。这是由于信道的传输特性造成的。均衡器电路通过整形接收到的脉冲来补偿这些损失。

定时电路

为了获得高质量的输出，应该在信噪比 (SNR) 最大的地方对脉冲进行采样。为了实现这种完美的采样，必须从接收到的脉冲中导出一个周期性脉冲序列，这是由定时电路完成的。

因此，定时电路通过接收到的脉冲，为在高 SNR 下采样分配定时间隔。

决策设备

定时电路确定采样时间。决策设备在这些采样时间被启用。决策设备根据量化脉冲和噪声的幅度是否超过预定值来决定其输出。

这些是数字通信中使用的一些技术。还有其他重要的技术需要学习，称为数据编码技术。在了解线路代码之后，我们将在后续章节中学习这些内容。

数字通信 - 线路码

**线路码**是在传输线上传输数字信号时使用的数据传输码。选择这种编码过程是为了避免信号重叠和失真，例如符号间干扰。

线路编码的特性

以下是线路编码的特性：

由于编码是为了使更多比特在一个信号上传输，因此使用的带宽大大减少。
对于给定的带宽，功率得到有效利用。
误差概率大大降低。
进行错误检测，双极性也具有纠错能力。
功率密度更有利。
定时内容足够。
避免长时间的“**1**”和“**0**”字符串以保持透明性。

线路编码的类型

线路编码有3种类型

单极性
极性
双极性

单极性信号

单极性信号也称为开关键控或简称为OOK。

脉冲的存在表示1，脉冲的不存在表示0。

单极性信号有两种变体：

不归零 (NRZ)
归零 (RZ)

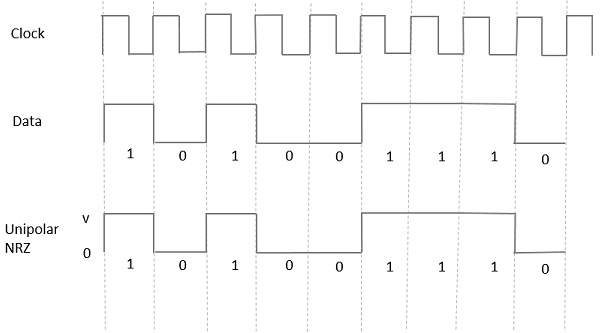
单极性不归零 (NRZ)

在这种类型的单极性信号中，数据中的高电平由称为标记的正脉冲表示，其持续时间T₀等于符号位持续时间。数据输入中的低电平没有脉冲。

下图清楚地描述了这一点。

优点

单极性NRZ的优点是：

它很简单。
需要较少的带宽。

缺点

单极性NRZ的缺点是：

没有错误校正。
低频分量的存在可能会导致信号下垂。
没有时钟。
容易发生同步丢失（尤其是在1和0的长串情况下）。

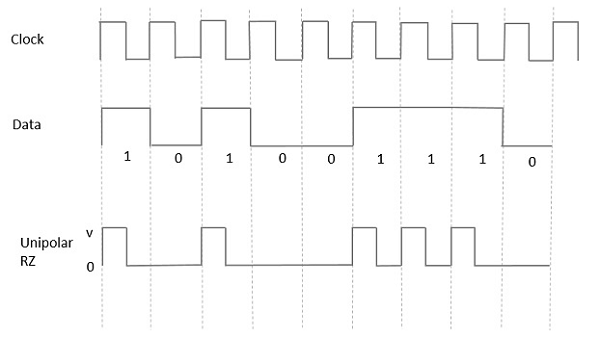
单极性归零 (RZ)

在这种类型的单极性信号中，数据中的高电平虽然由标记脉冲表示，但其持续时间T₀小于符号位持续时间。位持续时间的一半保持高电平，但它立即返回到零，并在位持续时间的剩余一半显示脉冲不存在。

借助下图可以清楚地理解这一点。

优点

单极性RZ的优点是：

它很简单。
在符号速率处存在的谱线可用作时钟。

缺点

单极性RZ的缺点是：

没有错误校正。
占用单极性NRZ的两倍带宽。
在信号在0 Hz处非零的地方会产生信号下垂。

双极性信号

双极性信号有两种方法。它们是：

双极性NRZ
双极性RZ

双极性NRZ

在这种类型的双极性信号中，数据中的高电平由正脉冲表示，而数据中的低电平由负脉冲表示。下图很好地描述了这一点。

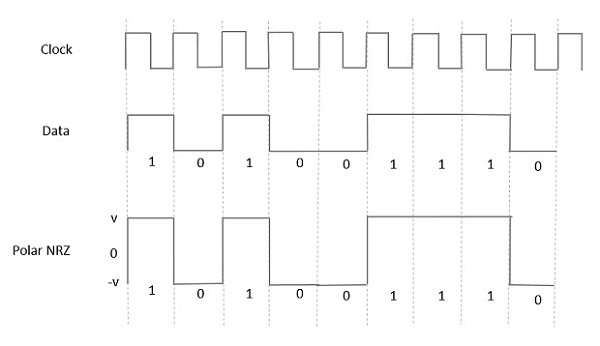
优点

双极性NRZ的优点是：

它很简单。
不存在低频分量。

缺点

双极性NRZ的缺点是：

没有错误校正。
没有时钟。
在信号在0 Hz处非零的地方会产生信号下垂。

双极性RZ

在这种类型的双极性信号中，数据中的高电平虽然由标记脉冲表示，但其持续时间T₀小于符号位持续时间。位持续时间的一半保持高电平，但它立即返回到零，并在位持续时间的剩余一半显示脉冲不存在。

但是，对于低电平输入，负脉冲表示数据，零电平在位持续时间的另一半保持不变。下图清楚地描述了这一点。

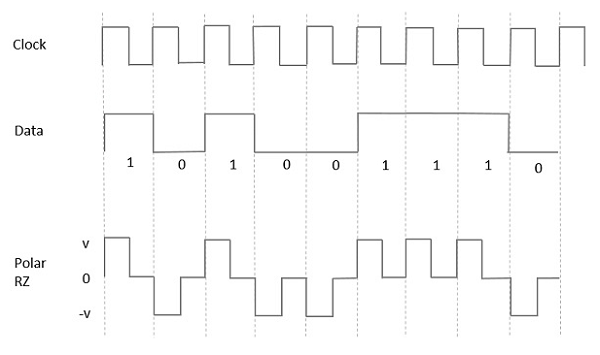
优点

双极性RZ的优点是：

它很简单。
不存在低频分量。

缺点

双极性RZ的缺点是：

没有错误校正。
没有时钟。
占用双极性NRZ的两倍带宽。
在信号在0 Hz处非零的地方会产生信号下垂。

双极性信号

这是一种编码技术，它具有三个电压电平，即+、-和0。这种信号称为双二进制信号。

此类型的一个示例是交替标记反转 (AMI)。对于1，电压电平从+到-或从-到+发生转换，交替的1具有相同的极性。0将具有零电压电平。

即使在这种方法中，我们也有两种类型。

双极性NRZ
双极性RZ

从目前为止讨论的模型中，我们了解了NRZ和RZ之间的区别。这里也是一样的。下图清楚地描述了这一点。

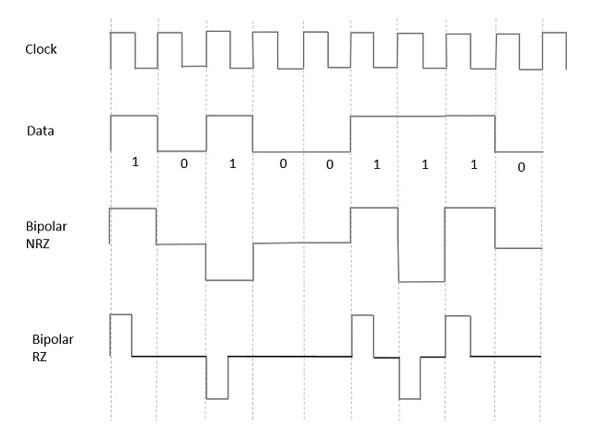
上图同时显示了双极性NRZ和RZ波形。NRZ类型的脉冲持续时间和符号位持续时间相等，而RZ类型的脉冲持续时间是符号位持续时间的一半。

优点

以下是优点：

它很简单。
不存在低频分量。
比单极性和双极性NRZ方案占用更低的带宽。
此技术适用于通过AC耦合线路传输，因为这里不会发生信号下垂。
此方法具有单错误检测能力。

缺点

以下是缺点：

没有时钟。
长串数据会导致同步丢失。

功率谱密度

描述信号的功率如何在频域的各种频率上分布的函数称为功率谱密度 (PSD)。

PSD是自相关（观测值之间的相似性）的傅里叶变换。它呈矩形脉冲的形式。

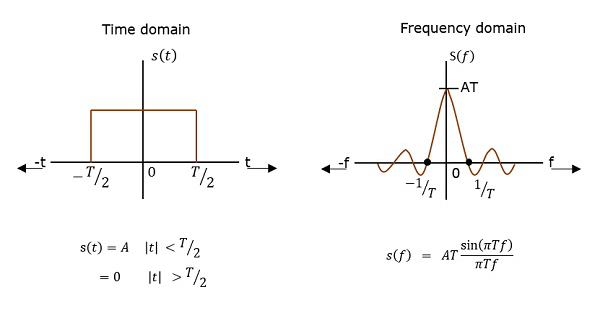
PSD推导

根据爱因斯坦-维纳-辛钦定理，如果已知随机过程的自相关函数或功率谱密度，则可以精确地找到另一个。

因此，为了推导功率谱密度，我们将使用功率信号x(t)的时间自相关(R_x(τ))，如下所示。

R_x(τ) = lim_{T_p→∞}(1/T_p)∫_{-T_p/2}^T_p/2x(t)x(t+τ)dt

由于x(t)由脉冲组成，R_x(τ)可以写成

R_x(τ) = (1/T)∑_n=-∞^∞R_nδ(τ-nT)

其中R_n = lim_N→∞(1/N)∑_ka_ka_k+n

已知对于实信号R_n = R_-n，我们有

S_x(w) = (1/T)(R₀ + 2∑_n=1^∞R_ncosnwT)

由于脉冲滤波器的频谱为(w)↔f(t)，我们有

s_y(w) = |F(w)|²S_x(w)

= |F(w)|²/T(∑_n=-∞^∞R_ne^-jnwT_b)

= |F(w)|²/T(R₀ + 2∑_n=1^∞R_ncosnwT)

因此，我们得到了功率谱密度的方程。利用这个方程，我们可以找到各种线路码的PSD。

数据编码技术

编码是将数据或给定的字符、符号、字母等序列转换为指定格式的过程，用于安全传输数据。解码是编码的反向过程，用于从转换后的格式中提取信息。

数据编码

编码是使用各种电压或电流电平模式来表示传输链路上数字信号的1和0的过程。

常见的线路编码类型包括单极性、双极性、双极性和曼彻斯特编码。

编码技术

根据数据转换的类型，数据编码技术分为以下几种类型。

模拟数据到模拟信号 - 模拟信号的调幅、调频和调相等调制技术属于此类。
模拟数据到数字信号 - 此过程可以称为数字化，通过脉冲编码调制 (PCM) 完成。因此，它只不过是数字调制。正如我们已经讨论过的，采样和量化是其中的重要因素。增量调制比PCM提供更好的输出。
数字数据到模拟信号 - 幅移键控 (ASK)、频移键控 (FSK)、相移键控 (PSK) 等调制技术属于此类。这些将在后续章节中讨论。
数字数据到数字信号 - 这些都包含在本节中。有多种方法可以将数字数据映射到数字信号。其中一些是：

不归零 (NRZ)

NRZ码对高电压电平使用1，对低电压电平使用0。NRZ码的主要特性是电压电平在位区间保持恒定。不会指示位的结束或开始，如果前一位的值和当前位的值相同，它将保持相同的电压状态。

下图解释了NRZ编码的概念。

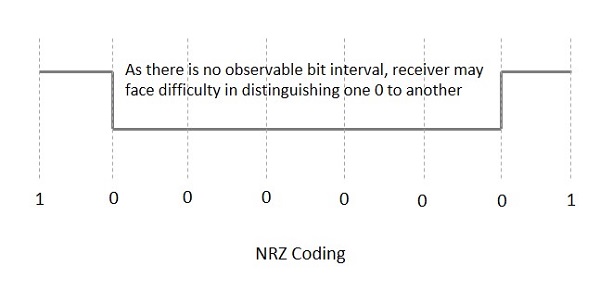
如果考虑上述示例，由于存在长时间的恒定电压电平序列，并且由于缺少位间隔可能会丢失时钟同步，接收器难以区分0和1。

NRZ有两种变体，即：

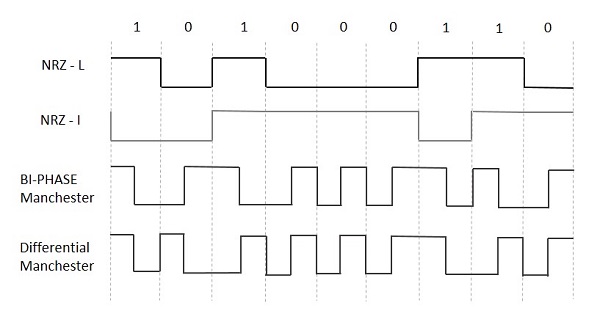
NRZ-L（NRZ-电平）

只有当输入信号从1变为0或从0变为1时，信号的极性才会发生变化。它与NRZ相同，但是输入信号的第一位应该改变极性。

NRZ-I（NRZ-反相）

如果输入信号出现1，则在位间隔的开始处会发生转换。对于输入信号的0，在位间隔的开始处不会发生转换。

NRZ码的缺点是，当存在1和0的字符串时，发射机时钟与接收机时钟的同步将完全被打乱。因此，需要提供单独的时钟线。

双相编码

每位时间检查信号电平两次，分别在初始和中间。因此，时钟速率是数据传输速率的两倍，因此调制速率也是两倍。时钟来自信号本身。这种编码所需的带宽更大。

双相编码有两种类型。

曼彻斯特双相
差分曼彻斯特

曼彻斯特双相

在这种编码类型中，转换在位间隔的中间进行。对于输入位1，结果脉冲的转换在间隔中间从高到低。而对于输入位0，转换是从低到高。

差分曼彻斯特

在这种编码类型中，总是在位间隔的中间发生转换。如果在位间隔的开始处发生转换，则输入位为0。如果在位间隔的开始处没有发生转换，则输入位为1。

下图说明了针对不同数字输入的NRZ-L、NRZ-I、双相曼彻斯特和差分曼彻斯特编码的波形。

分组码

在分组码类型中，著名的有4B/5B编码和8B/6T编码。在这两种过程中，位数的处理方式不同。

4B/5B编码

在曼彻斯特编码中，要发送数据，需要比NRZ编码快两倍的时钟。顾名思义，这里将4位代码与5位代码映射，组中1位的数量最少。

通过为每4个连续位的块分配一个等效的5位字，避免了NRZ-I编码中的时钟同步问题。这些5位字在一个字典中预先确定。

选择5位代码的基本思想是，它应该以0开头，并且最多有两个尾随0。因此，选择这些字是为了确保每位块发生两次事务。

8B/6T编码

我们使用了两个电压电平来通过单个信号发送单个位。但是，如果我们使用超过3个电压电平，我们可以通过单个信号发送更多位。

例如，如果使用6个电压电平在一个信号上表示8位，则这种编码称为8B/6T编码。因此，在这种方法中，我们有多达729 (3^6)个信号组合和256 (2^8)个位组合。

这些技术主要用于通过压缩或编码数字数据将其转换为数字信号，以便可靠地传输数据。

数字通信 - 脉冲整形

在学习了不同类型的编码技术之后，我们了解了数据如何容易失真，以及为防止数据受到影响而采取的措施，以便建立可靠的通信。

还有一种很可能发生的重要的失真，称为**符号间干扰 (ISI)**。

符号间干扰

这是一种信号失真形式，其中一个或多个符号会干扰后续信号，从而产生噪声或导致输出质量差。

ISI 的原因

ISI 的主要原因是：

多径传播
信道中的非线性频率响应

ISI 是不需要的，应该完全消除以获得干净的输出。为了减轻其影响，也应该解决导致 ISI 的原因。

为了查看接收机输出中存在的 ISI 的数学形式，我们可以考虑接收机输出。

接收滤波器的输出 $y(t)$ 在时间 $t_i = iT_b$（其中**i**取整数值）进行采样，得到：

$y(t_i) = \mu \displaystyle\sum\limits_{k = -\infty}^{\infty}a_kp(iT_b - kT_b)$

$= \mu a_i + \mu \displaystyle\sum\limits_{k = -\infty \\ k \neq i}^{\infty}a_kp(iT_b - kT_b)$

在上式中，第一项 $\mu a_i$ 由第**i**个发送的比特产生。

第二项表示所有其他发送的比特对第**i**个比特解码的残留影响。这种残留影响称为**符号间干扰**。

在没有 ISI 的情况下，输出将为：

$$y(t_i) = \mu a_i$$

此方程表明，正确地再现了第**i**个发送的比特。但是，ISI 的存在会在输出中引入比特错误和失真。

在设计发射机或接收机时，重要的是要尽量减少 ISI 的影响，以便以尽可能低的错误率接收输出。

眼图

研究 ISI 影响的一种有效方法是**眼图**。眼图的名称来源于其对于二进制波形的类似人眼的形状。眼图的内部区域称为**眼图开口**。下图显示了眼图的图像。

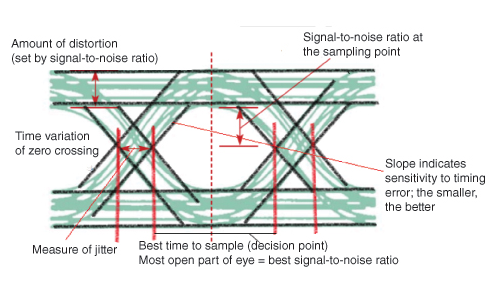
**抖动**是数字信号瞬时偏离其理想位置的短期变化，这可能会导致数据错误。

当 ISI 的影响增加时，从眼图开口的上部到下部的轨迹会增加，如果 ISI 非常高，眼图将完全闭合。

眼图提供有关特定系统的信息。

实际眼图用于估计误码率和信噪比。
眼图开口的宽度定义了可以在不产生 ISI 误差的情况下对接收波进行采样的时间间隔。
眼图开口最宽的时刻将是优选的采样时间。
根据采样时间，眼图闭合的速度决定了系统对定时误差的敏感程度。
在指定的采样时间，眼图开口的高度定义了噪声裕度。

因此，眼图的解释是一个重要的考虑因素。

均衡

为了建立可靠的通信，我们需要高质量的输出。必须处理信道的传输损耗和其他影响信号质量的因素。正如我们所讨论的，最常见的损耗是 ISI。

为了使信号免受 ISI 的影响，并确保最大信噪比，我们需要实现一种称为**均衡**的方法。下图显示了通信系统接收部分中的均衡器。

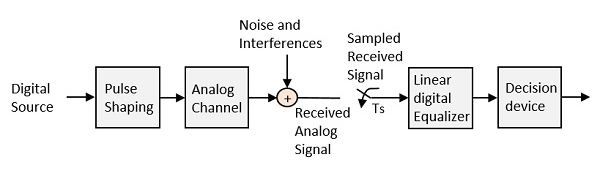
图中所示的噪声和干扰在传输过程中很可能发生。再生中继器具有均衡器电路，该电路通过整形电路来补偿传输损耗。均衡器是可行的。

误码率和品质因数

可以通信数据的速率称为**数据速率**。在传输数据时比特中发生的错误速率称为**误码率 (BER)**。

BER 发生的概率是**误码概率**。信噪比 (SNR) 的提高会降低 BER，因此误码概率也会降低。

在模拟接收器中，检测过程中的**品质因数**可以定义为输出 SNR 与输入 SNR 的比率。较高的品质因数将是有利的。

数字调制技术

数字到模拟信号是本章接下来将讨论的转换。这些技术也称为**数字调制技术**。

**数字调制**提供更大的信息容量、更高的数据安全性、更快的系统可用性和高质量的通信。因此，数字调制技术因其比模拟调制技术能够传输更大数据量而需求量更大。

根据需要，存在许多类型的数字调制技术及其组合。在所有这些技术中，我们将讨论一些突出的技术。

ASK – 幅移键控

结果输出的幅度取决于输入数据，即它应该是零电平还是正负变化，这取决于载波频率。

FSK – 频移键控

输出信号的频率将根据应用的输入数据而变高或变低。

PSK – 相移键控

输出信号的相位将根据输入而发生变化。根据相移的数量，它们主要分为两种类型，即二进制相移键控 (BPSK) 和正交相移键控 (QPSK)。另一种是差分相移键控 (DPSK)，它根据前一个值改变相位。

M进制编码

M 进制编码技术是在单个信号上同时传输多个比特的方法。这有助于减少带宽。

M 进制技术的类型包括：

M 进制 ASK
M 进制 FSK
M 进制 PSK

所有这些都将在后续章节中讨论。

幅移键控

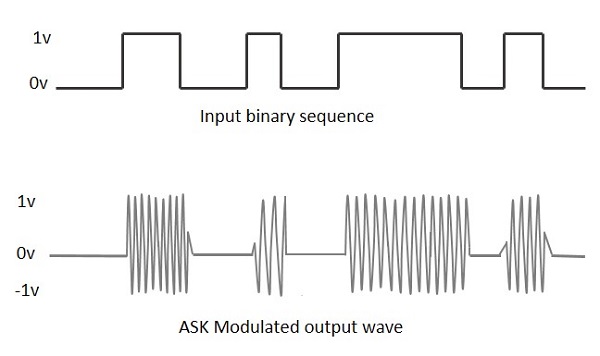
**幅移键控 (ASK)** 是一种幅度调制，它以信号幅度的变化形式表示二进制数据。

任何调制信号都具有高频载波。当 ASK 调制时，二进制信号在**低**输入时给出**零**值，而在**高**输入时给出**载波输出**。

下图显示了 ASK 调制波形及其输入。

为了了解获得这种 ASK 调制波的过程，让我们学习 ASK 调制器的原理。

ASK 调制器

ASK 调制器框图包括载波信号发生器、来自消息信号的二进制序列和带限滤波器。以下是 ASK 调制器的框图。

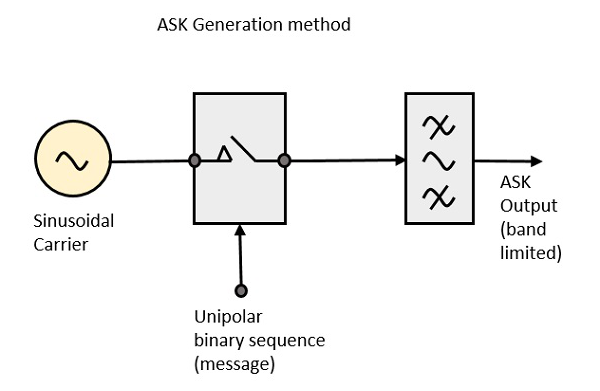
载波发生器发送连续的高频载波。来自消息信号的二进制序列使单极性输入变为高或低。高信号闭合开关，允许载波波。因此，输出将是高输入下的载波信号。当输入低时，开关打开，不允许出现电压。因此，输出将为低。

带限滤波器根据带限滤波器或脉冲整形滤波器的幅度和相位特性来整形脉冲。

ASK 解调器

有两种类型的 ASK 解调技术。它们是：

异步 ASK 解调/检测
同步 ASK 解调/检测

当发射机的时钟频率与接收机的时钟频率匹配时，这被称为**同步方法**，因为频率已同步。否则，它被称为**异步**。

异步 ASK 解调器

异步 ASK 检测器由半波整流器、低通滤波器和比较器组成。以下是相同的框图。

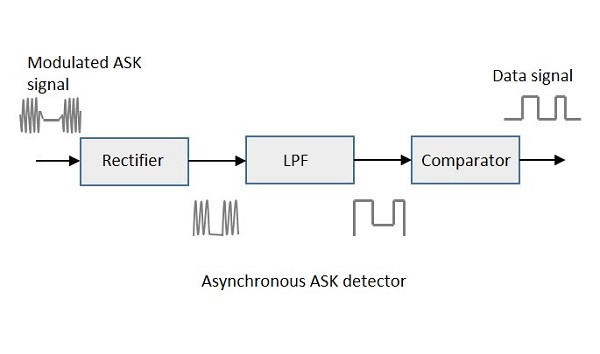
调制的 ASK 信号被馈送到半波整流器，半波整流器提供正半波输出。低通滤波器抑制较高的频率，并提供包络检波输出，比较器从中提供数字输出。

同步 ASK 解调器

同步 ASK 检测器由平方律检测器、低通滤波器、比较器和电压限制器组成。以下是相同的框图。

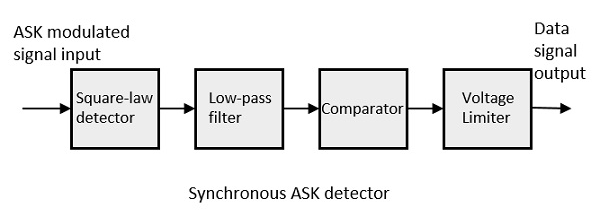
ASK 调制输入信号被馈送到平方律检测器。平方律检测器的输出电压与幅度调制输入电压的平方成正比。低通滤波器最小化较高的频率。比较器和电压限制器有助于获得干净的数字输出。

频移键控

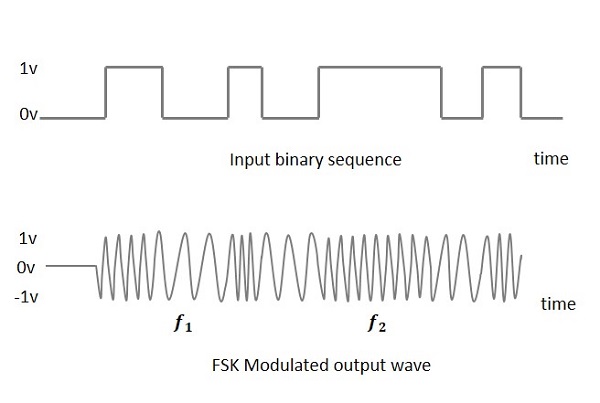
**频移键控 (FSK)** 是一种数字调制技术，其中载波信号的频率根据数字信号的变化而变化。FSK 是一种频移键控方案。

FSK调制波的输出，对于二进制高电平输入，频率较高；对于二进制低电平输入，频率较低。二进制的1和0分别称为标记频率（Mark frequency）和间隔频率（Space frequency）。

下图是FSK调制波形及其输入的示意图。

为了了解获得此FSK调制波的过程，让我们了解一下FSK调制器的工作原理。

FSK调制器

FSK调制器的框图包括两个振荡器、一个时钟和二进制输入序列。以下是其框图。

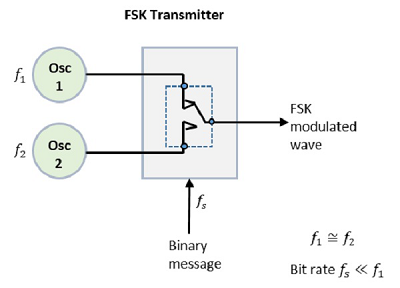
两个振荡器产生高频和低频信号，它们与一个开关和一个内部时钟连接。为了避免在消息传输过程中输出波形的突变相位不连续性，内部向两个振荡器都施加了时钟。二进制输入序列被应用于发射器，以便根据二进制输入选择频率。

FSK解调器

解调FSK波的方法有很多种。FSK检测的主要方法是异步检测器和同步检测器。同步检测器是相干的，而异步检测器是非相干的。

异步FSK检测器

异步FSK检测器的框图由两个带通滤波器、两个包络检测器和一个判决电路组成。以下是示意图。

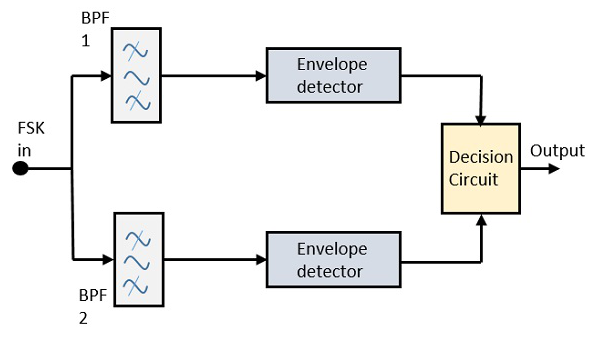
FSK信号通过两个调谐到间隔频率和标记频率的带通滤波器（BPF）。这两个BPF的输出看起来像ASK信号，该信号被送入包络检测器。每个包络检测器中的信号都是异步调制的。

判决电路选择哪个输出更可能，并从任一个包络检测器中选择它。它还将波形重新整形为矩形波。

同步FSK检测器

同步FSK检测器的框图由两个带本地振荡器电路的混频器、两个带通滤波器和一个判决电路组成。以下是示意图。

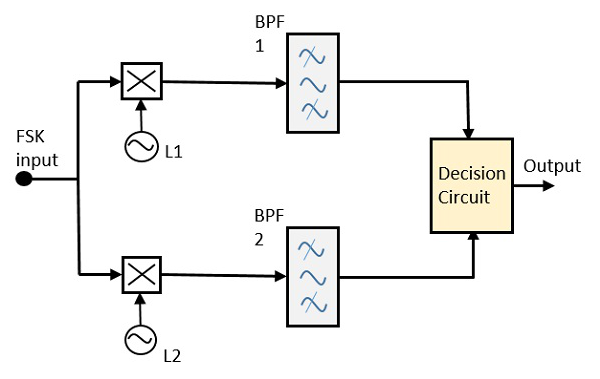
FSK信号输入被送入两个带本地振荡器电路的混频器。这两个混频器连接到两个带通滤波器。这些组合充当解调器，判决电路选择哪个输出更可能，并从任一个检测器中选择它。两个信号具有最小的频率间隔。

对于这两个解调器，每个解调器的带宽都取决于它们的比特率。这种同步解调器比异步解调器复杂一些。

数字通信 - 相移键控

相移键控 (PSK) 是一种数字调制技术，其中通过在特定时间改变正弦和余弦输入来改变载波信号的相位。PSK技术广泛应用于无线局域网、生物识别、非接触式操作以及RFID和蓝牙通信。

PSK根据信号的相移分为两种类型：

二进制相移键控 (BPSK)

这也被称为2相PSK或相位反转键控。在这种技术中，正弦波载波进行两次相位反转，例如0°和180°。

对于消息为数字信息，BPSK基本上是一种双边带抑制载波 (DSBSC) 调制方案。

正交相移键控 (QPSK)

这是一种相移键控技术，其中正弦波载波进行四次相位反转，例如0°、90°、180°和270°。

如果进一步扩展此类技术，则PSK也可以通过八个或十六个值来完成，具体取决于需求。

BPSK调制器

二进制相移键控的框图包括平衡调制器，该调制器的一个输入是载波正弦波，另一个输入是二进制序列。以下是示意图。

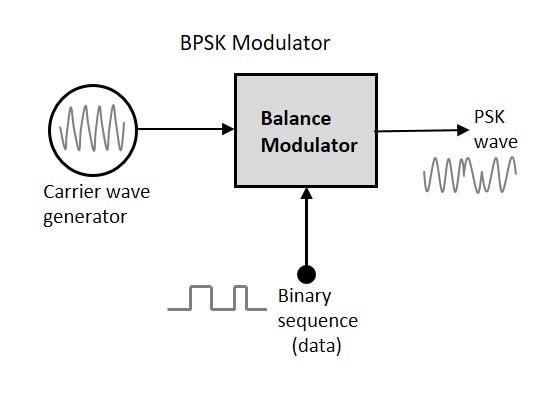
BPSK的调制是使用平衡调制器完成的，它将施加在输入端的两个信号相乘。对于零二进制输入，相位将为0°；对于高电平输入，相位反转为180°。

以下是BPSK调制输出波形及其给定输入的示意图。

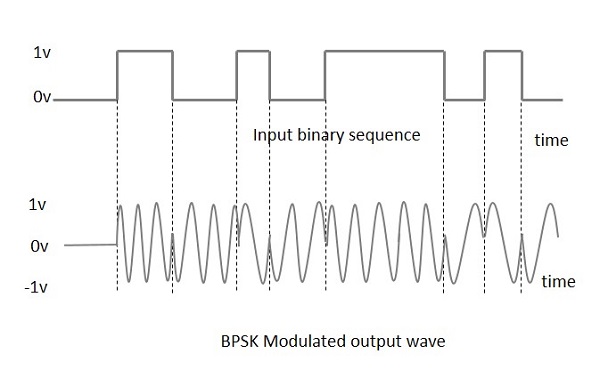
调制器的输出正弦波将是直接输入载波或反相（180°相移）输入载波，它是数据信号的函数。

BPSK解调器

BPSK解调器的框图包括一个带本地振荡器电路的混频器、一个带通滤波器和一个双输入检测电路。图如下所示。

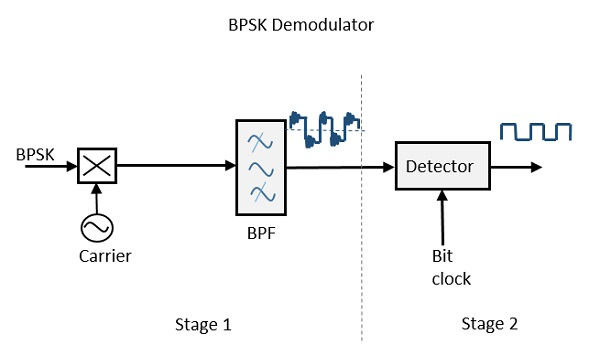
通过在混频器电路和带通滤波器的帮助下恢复带限消息信号，解调的第一阶段完成。获得带限基带信号，并使用此信号来再生二进制消息比特流。

在解调的下一阶段，检测电路需要比特时钟速率来产生原始的二进制消息信号。如果比特率是载波频率的子倍数，则比特时钟再生将简化。为了使电路更容易理解，也可以在检测的第二阶段插入一个决策电路。

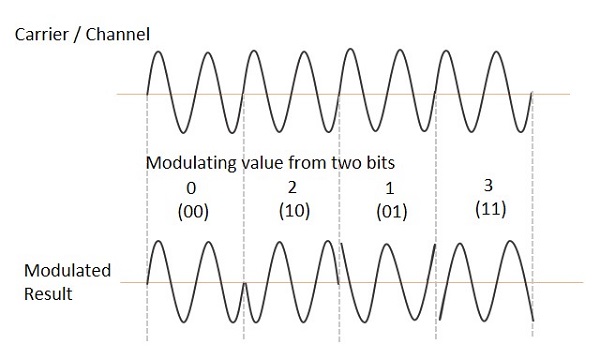
正交相移键控

正交相移键控 (QPSK) 是BPSK的一种变体，它也是一种双边带抑制载波 (DSBSC) 调制方案，它一次发送两位数字信息，称为双比特 (bigits)。

它不是将数字比特转换为一系列数字流，而是将它们转换为比特对。这将数据比特率降低了一半，从而为其他用户留出空间。

QPSK调制器

QPSK调制器使用比特分割器、两个带本地振荡器的乘法器、一个2比特串行到并行转换器和一个求和电路。以下是相同的框图。

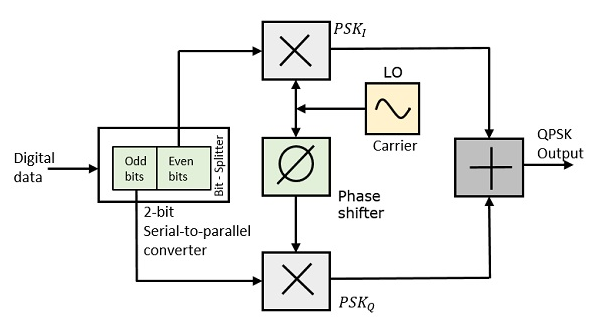
在调制器的输入端，消息信号的偶数比特（即第2位、第4位、第6位等）和奇数比特（即第1位、第3位、第5位等）通过比特分割器分离，并与相同的载波相乘以产生奇数BPSK（称为PSK_I）和偶数BPSK（称为PSK_Q）。PSK_Q信号在调制前以90°的相位进行移位。

针对两位输入的QPSK波形如下所示，它显示了不同二进制输入的调制结果。

QPSK解调器

QPSK解调器使用两个带本地振荡器的乘积解调器电路、两个带通滤波器、两个积分器电路和一个2比特并行到串行转换器。以下是相同的框图。

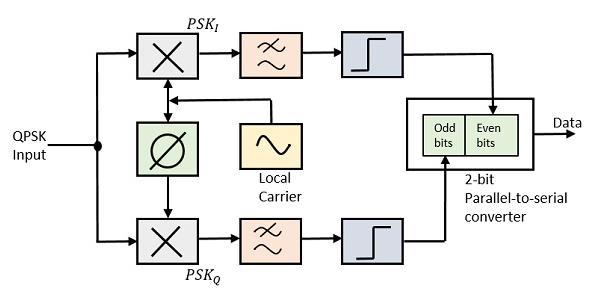
解调器输入端的两个乘积检测器同时解调两个BPSK信号。此处从原始数据中恢复比特对。这些信号经过处理后，被传递到并行到串行转换器。

差分相移键控

在差分相移键控 (DPSK) 中，调制信号的相位相对于前一个信号元素发生偏移。这里没有考虑参考信号。信号相位遵循前一个元素的高或低状态。这种DPSK技术不需要参考振荡器。

下图表示DPSK的模型波形。

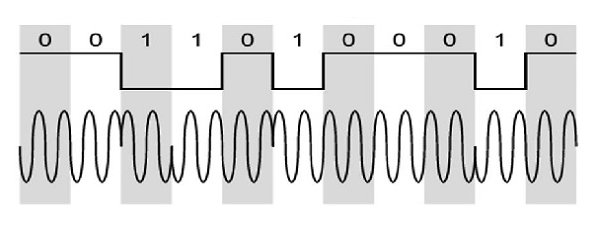
从上图可以看出，如果数据位为低电平，即0，则信号相位不反转，而是继续保持不变。如果数据为高电平，即1，则信号相位反转，与NRZI一样，在1时反转（一种差分编码）。

如果我们观察上面的波形，我们可以说高状态在调制信号中表示M，低状态在调制信号中表示W。

DPSK调制器

DPSK是BPSK的一种技术，其中没有参考相位信号。在这里，发射信号本身可以用作参考信号。以下是DPSK调制器的框图。

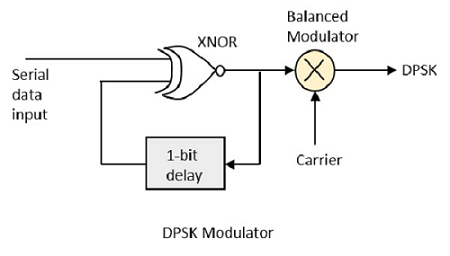
DPSK编码两个不同的信号，即载波和调制信号，每个信号都具有180°的相移。串行数据输入被送入异或非门，输出通过1位延迟再次反馈到另一个输入。异或非门的输出与载波信号一起送入平衡调制器，以产生DPSK调制信号。

DPSK解调器

在DPSK解调器中，反转位的相位与前一位的相位进行比较。以下是DPSK解调器的框图。

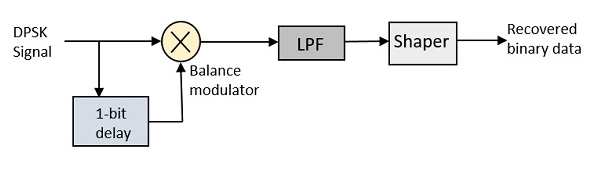
从上图可以看出，平衡调制器接收DPSK信号以及1位延迟输入。该信号借助低通滤波器 (LPF) 被限制在较低的频率范围内。然后将其传递到整形电路（比较器或施密特触发器电路），以恢复原始二进制数据作为输出。

数字通信 - M进制编码

单词二进制表示两位。M 代表一个数字，它对应于给定数量的二进制变量可能存在的条件、级别或组合的数量。

这是一种用于数据传输的数字调制技术，其中一次传输两位或更多位而不是一位。由于使用单个信号进行多比特传输，因此信道带宽降低。

M进制方程

如果数字信号处于四种状态下，例如电压电平、频率、相位和幅度，则M = 4。

产生给定数量条件所需的比特数可以用数学表达式表示为

$$N = \log_{2}{M}$$

其中

N 是所需的比特数

M 是使用N位可能存在的条件、级别或组合的数量。

上述方程可以重新排列为

$$2^N = M$$

例如，使用两位，2² = 4 种条件是可能的。

M进制技术的类型

一般来说，多电平 (M进制) 调制技术用于数字通信，因为允许在发射器的输入端使用具有两个以上调制电平的数字输入。因此，这些技术具有带宽效率。

有很多M进制调制技术。其中一些技术调制载波信号的一个参数，例如幅度、相位和频率。

M 进制 ASK

这称为M进制振幅移键 (M-ASK) 或M进制脉冲幅度调制 (PAM)。

载波信号的幅度采用M个不同的电平。

M进制ASK的表示

$S_m(t) = A_mcos (2 \pi f_ct) \quad A_m\epsilon {(2m - 1 - M) \Delta, m = 1,2... \: .M} \quad and \quad 0 \leq t \leq T_s$

M进制ASK的一些突出特点是：

此方法也用于PAM。
它的实现很简单。
M进制ASK易受噪声和失真的影响。

M 进制 FSK

这称为M进制频移键控 (M-ary FSK)。

载波信号的频率采用M个不同的电平。

M进制FSK的表示

$S_i(t) = \sqrt{\frac{2E_s}{T_s}} \cos \left ( \frac{\pi}{T_s}\left (n_c+i\right )t\right )$ $0 \leq t \leq T_s \quad and \quad i = 1,2,3... \: ..M$

其中，对于某个固定整数n，$f_c = \frac{n_c}{2T_s}$。

M进制FSK的一些突出特点是：

不像ASK那样容易受到噪声的影响。
传输的M个信号在能量和持续时间上是相等的。
信号间隔为$\frac{1}{2T_s}$ Hz，使信号彼此正交。
由于M个信号是正交的，因此信号空间中没有拥挤。
随着M的增加，M进制FSK的带宽效率降低，功率效率提高。

M 进制 PSK

这被称为M进制相移键控（M-ary PSK）。

载波信号的相位取M个不同的级别。

M进制PSK的表示

$S_i(t) = \sqrt{\frac{2E}{T}} \cos \left (w_o t + \phi _it\right )$ $0 \leq t \leq T \quad and \quad i = 1,2 ... M$

$$\phi _i \left ( t \right ) = \frac{2 \pi i}{M} \quad where \quad i = 1,2,3 ... \: ...M$$

M进制PSK的一些突出特点是：

包络恒定，相位可能性更多。
这种方法在早期空间通信中使用。
性能优于ASK和FSK。
接收端的相位估计误差最小。
M进制PSK的带宽效率随着M的增加而降低，功率效率随着M的增加而提高。

到目前为止，我们已经讨论了不同的调制技术。所有这些技术的输出都是一个二进制序列，表示为1和0。这种二进制或数字信息有很多类型和形式，将在后面讨论。

数字通信 - 信息论

信息是通信系统的源头，无论是模拟的还是数字的。信息论是一种对信息编码以及信息的量化、存储和通信进行研究的数学方法。

事件发生的条件

如果我们考虑一个事件，则有三个发生的条件。

如果事件没有发生，则存在不确定性的条件。
如果事件刚刚发生，则存在意外性的条件。
如果事件发生了一段时间，则存在一些信息的条件。

这三个事件发生在不同的时间。这些条件的差异有助于我们了解事件发生概率的知识。

熵

当我们观察事件发生的可能性时，它有多么令人惊讶或不确定，这意味着我们试图了解事件源的平均信息量。

熵可以定义为每个信源符号的平均信息量的度量。“信息论之父”克劳德·香农为此提供了一个公式：

$$H = - \sum_{i} p_i \log_{b}p_i$$

其中p_i是给定字符流中字符编号i出现的概率，b是所用算法的基数。因此，这也称为香农熵。

观察信道输出后，关于信道输入剩余的不确定性量称为条件熵。它用$H(x \mid y)$表示。

互信息

让我们考虑一个输出为Y，输入为X的信道。

设先验不确定性的熵为X = H(x)

（这假设在输入应用之前）。

为了了解应用输入后输出的不确定性，让我们考虑条件熵，假设Y = y_k

$$H\left ( x\mid y_k \right ) = \sum_{j = 0}^{j - 1}p\left ( x_j \mid y_k \right )\log_{2}\left [ \frac{1}{p(x_j \mid y_k)} \right ]$$

这是一个关于$H(X \mid y = y_0) \: ... \: ... \: ... \: ... \: ... \: H(X \mid y = y_k)$的随机变量，其概率分别为$p(y_0) \: ... \: ... \: ... \: ... \: p(y_{k-1})$。

输出字母表y的$H(X \mid y = y_k)$的均值为：

$H\left ( X\mid Y \right ) = \displaystyle\sum\limits_{k = 0}^{k - 1}H\left ( X \mid y=y_k \right )p\left ( y_k \right )$

$= \displaystyle\sum\limits_{k = 0}^{k - 1} \displaystyle\sum\limits_{j = 0}^{j - 1}p\left (x_j \mid y_k \right )p\left ( y_k \right )\log_{2}\left [ \frac{1}{p\left ( x_j \mid y_k \right )} \right ]$

$= \displaystyle\sum\limits_{k = 0}^{k - 1} \displaystyle\sum\limits_{j = 0}^{j - 1}p\left (x_j ,y_k \right )\log_{2}\left [ \frac{1}{p\left ( x_j \mid y_k \right )} \right ]$

现在，考虑这两种不确定性条件（应用输入之前和之后），我们知道它们的差，即$H(x) - H(x \mid y)$必须表示通过观察信道输出而解决的关于信道输入的不确定性。

这称为信道的互信息。

将互信息表示为$I(x;y)$，我们可以将整个内容写成一个方程，如下所示：

$$I(x;y) = H(x) - H(x \mid y)$$

因此，这是互信息的方程表示。

互信息的性质

这些是互信息的性质。

信道的互信息是对称的。

$$I(x;y) = I(y;x)$$
互信息是非负的。

$$I(x;y) \geq 0$$
互信息可以用信道输出的熵来表示。

$$I(x;y) = H(y) - H(y \mid x)$$

其中$H(y \mid x)$是条件熵。
信道的互信息与信道输入和信道输出的联合熵有关。

$$I(x;y) = H(x)+H(y) - H(x,y)$$

其中联合熵$H(x,y)$定义为：

$$H(x,y) = \displaystyle\sum\limits_{j=0}^{j-1} \displaystyle\sum\limits_{k=0}^{k-1}p(x_j,y_k)\log_{2} \left ( \frac{1}{p\left ( x_i,y_k \right )} \right )$$

信道容量

到目前为止，我们已经讨论了互信息。当通过离散无记忆信道传输时，在信号间隔的瞬间，最大平均互信息，最大可靠数据传输速率的概率，可以理解为信道容量。

它用C表示，以每信道比特为单位测量。

离散无记忆信源

一个信源，其数据在连续间隔发出，并且与先前值无关，可以称为离散无记忆信源。

该信源是离散的，因为它不被认为是连续时间间隔，而是在离散时间间隔。该信源是无记忆的，因为它在每个时刻都是新的，不考虑先前的值。

信源编码定理

离散无记忆信源产生的码必须有效地表示，这是通信中的一个重要问题。为了实现这一点，有一些码字来表示这些信源码。

例如，在电报中，我们使用莫尔斯电码，其中字母用点和划表示。如果考虑字母E，它使用最多，则表示为“.”而字母Q很少使用，表示为“--.-”

让我们看一下框图。

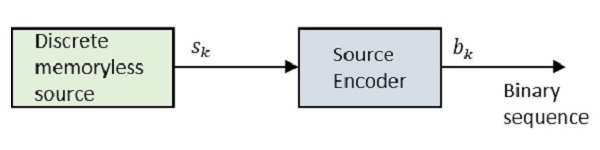
其中S_k是离散无记忆信源的输出，b_k是信源编码器的输出，用0和1表示。

编码后的序列可以方便地在接收端解码。

让我们假设信源有一个具有k个不同符号的字母表，并且第k个符号S_k出现的概率为P_k，其中k = 0, 1…k-1。

设编码器分配给符号S_k的二进制码字长度为l_k（以比特为单位）。

因此，我们将信源编码器的平均码字长度L定义为：

$$\overline{L} = \displaystyle\sum\limits_{k=0}^{k-1} p_kl_k$$

L表示每个信源符号的平均比特数。

如果$L_{min} = \: 最小可能值 \: of \: \overline{L}$

则编码效率可以定义为：

$$\eta = \frac{L{min}}{\overline{L}}$$

由于$\overline{L}\geq L_{min}$，我们将有$\eta \leq 1$

然而，当$\eta = 1$时，信源编码器被认为是有效的。

为此，必须确定$L_{min}$的值。

让我们参考定义：“给定一个熵为$H(\delta)$的离散无记忆信源，任何信源编码的平均码字长度L都受限于$\overline{L} \geq H(\delta)$。”

简单来说，码字（例如，单词QUEUE的莫尔斯电码是 -.- ..- . ..- . ）总是大于或等于信源码（例如QUEUE）。这意味着码字中的符号大于或等于信源码中的字母。

因此，用$L_{min} = H(\delta)$，信源编码器关于熵$H(\delta)$的效率可以写成：

$$\eta = \frac{H(\delta)}{\overline{L}}$$

这个信源编码定理被称为无噪声编码定理，因为它建立了无错误编码。它也称为香农第一定理。

信道编码定理

信道中存在的噪声会在数字通信系统的输入和输出序列之间产生不需要的错误。为了可靠的通信，错误概率应该非常低，几乎≤ 10^-6。

通信系统中的信道编码引入了具有控制的冗余，以提高系统的可靠性。信源编码减少了冗余以提高系统的效率。

信道编码包括两个部分的动作。

映射传入数据序列到信道输入序列。
逆映射信道输出序列到输出数据序列。

最终目标是最小化信道噪声的整体影响。

映射由发射机在编码器的帮助下完成，而逆映射由接收机中的解码器完成。

信道编码

让我们考虑一个熵为H (δ)的离散无记忆信道(δ)

T_s表示δ每秒提供的符号数

信道容量用C表示

信道每T_c秒可以使用一次

因此，信道的最大能力为C/T_c

发送的数据 = $\frac{H(\delta)}{T_s}$

如果$\frac{H(\delta)}{T_s} \leq \frac{C}{T_c}$，这意味着传输良好，并且可以以很小的错误概率重现。

其中，$\frac{C}{T_c}$是信道容量的临界速率。

如果$\frac{H(\delta)}{T_s} = \frac{C}{T_c}$，则系统被称为以临界速率进行信号传输。

相反，如果$\frac{H(\delta)}{T_s} > \frac{C}{T_c}$，则传输是不可能的。

因此，为了可靠的无错误消息，传输的最大速率等于信道容量的临界速率，这可以在离散无记忆信道上发生。这被称为信道编码定理。

数字通信 - 差错控制编码

噪声或错误是信号中的主要问题，它会干扰通信系统的可靠性。差错控制编码是用于控制错误发生的编码过程。这些技术有助于错误检测和错误纠正。

根据应用于它们的数学原理，存在许多不同的纠错码。但是，历史上，这些代码被分为线性分组码和卷积码。

线性分组码

在线性分组码中，奇偶校验位和消息位具有线性组合，这意味着生成的码字是任意两个码字的线性组合。

让我们考虑一些数据块，每个数据块包含k位。这些位映射到每个数据块包含n位的块中。这里n大于k。发送器添加冗余位，即(n-k)位。比率k/n是码率。它用r表示，r的值为r < 1。

这里添加的(n-k)位是奇偶校验位。奇偶校验位有助于错误检测和纠错，也有助于定位数据。在传输的数据中，码字的最左位对应于消息位，码字的最右位对应于奇偶校验位。

系统码

任何线性分组码都可以是系统码，除非它被修改。因此，未经修改的分组码称为系统码。

以下是根据分配情况的码字结构表示。

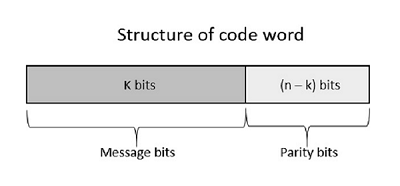
如果消息未被修改，则称为系统码。这意味着数据的加密不应改变数据。

卷积码

到目前为止，在线性码中，我们已经讨论了首选系统未修改码。这里，如果传输总共n位的数据，k位是消息位，(n-k)位是奇偶校验位。

在编码过程中，奇偶校验位从整个数据中减去，然后对消息位进行编码。现在，奇偶校验位再次被添加，整个数据再次被编码。

下图给出了用于信息传输的数据块和数据流的示例。

上述整个过程很繁琐，存在缺点。当系统繁忙时，缓冲区的分配是一个主要问题。

卷积码消除了这个缺点。其中，整个数据流被分配符号，然后传输。由于数据是比特流，因此不需要缓冲区来存储。

汉明码

码字的线性特性是两个码字的和也是一个码字。汉明码是一种线性纠错码，它可以检测多达两位错误，或者可以纠正一位错误，而不会检测到未纠正的错误。

使用汉明码时，使用额外的奇偶校验位来识别一位错误。为了从一个比特模式变为另一个比特模式，需要改变数据中的少量比特。此类比特数可以称为汉明距离。如果奇偶校验距离为2，则可以检测到一位翻转。但这无法纠正。此外，任何两位翻转都无法检测到。

然而，与前面讨论的方法相比，汉明码在错误检测和纠正方面是一个更好的方法。

BCH码

BCH码以发明者Bose、Chaudari和Hocquenghem的名字命名。在BCH码设计中，可以控制要纠正的符号数量，因此可以进行多比特纠正。BCH码是纠错码中一种强大的技术。

对于任何正整数m ≥ 3和t < 2^m-1，都存在一个BCH二进制码。以下是此类码的参数。

块长度n = 2^m-1

奇偶校验位数n - k ≤ mt

最小距离d_min ≥ 2t + 1

此码可以称为t错误纠正BCH码。

循环码

码字的循环特性是任何码字的循环移位也是一个码字。循环码遵循这种循环特性。

对于线性码C，如果每个码字，即C = (C1, C2, ...... Cn)来自C具有分量的循环右移，则它成为一个码字。这个右移等于n-1个循环左移。因此，它在任何移位下都是不变的。因此，线性码C，因为它在任何移位下都是不变的，可以称为循环码。

循环码用于纠错。它们主要用于纠正双重错误和突发错误。

因此，这些是在接收器处要检测的一些纠错码。这些码可以防止错误被引入并干扰通信。它们还可以防止信号被不需要的接收器窃听。下一章将讨论实现此目标的一类信令技术。

扩频调制

在传输信号之前，采用一类集合信令技术来提供安全的通信，称为扩频调制。扩频通信技术的主要优点是防止“干扰”，无论是有意的还是无意的。

采用这些技术调制的信号很难干扰，并且不能被阻塞。未经授权的入侵者绝不允许破解它们。因此，这些技术用于军事目的。这些扩频信号以低功率密度传输，并具有广泛的信号传播。

伪噪声序列

具有某些自相关特性的1和0的编码序列，称为伪噪声编码序列，用于扩频技术。它是一个最大长度序列，是一种循环码。

窄带和扩频信号

通过观察下图所示的频谱，可以很容易地理解窄带信号和扩频信号。

窄带信号

窄带信号的信号强度集中在下图的频谱图中所示。

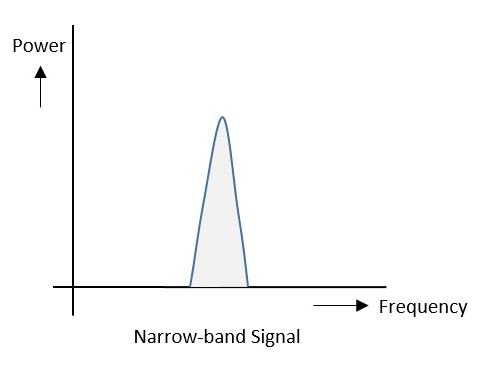
以下是一些特性：

信号带宽占据一个狭窄的频率范围。
功率密度高。
能量传播低且集中。

虽然特性良好，但这些信号容易受到干扰。

扩频信号

扩频信号的信号强度分布在下图的频谱图中所示。

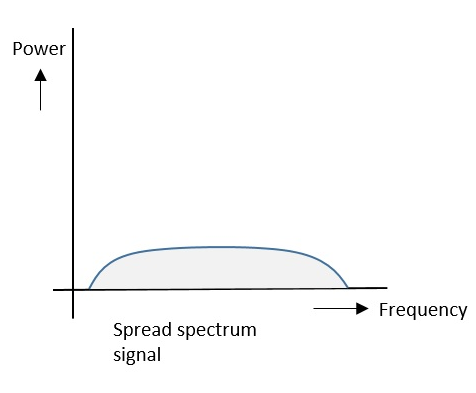
以下是一些特性：

信号带宽占据一个宽广的频率范围。
功率密度非常低。
能量广泛分布。

具有这些特性，扩频信号具有很强的抗干扰或抗阻塞能力。由于多个用户可以共享相同的扩频带宽而不会相互干扰，因此这些可以称为多址技术。

FHSS和DSSS/CDMA

扩频多址技术使用传输带宽大于最小所需射频带宽的信号。

它们分为两种类型。

跳频扩频 (FHSS)
直接序列扩频 (DSSS)

跳频扩频 (FHSS)

这是一种跳频技术，其中用户被要求在指定的时间间隔内从一个频率切换到另一个频率，因此称为跳频。例如，在特定时间段内向发送器1分配了一个频率。现在，一段时间后，发送器1跳到另一个频率，而发送器2使用发送器1先前使用的第一个频率。这称为频率复用。

数据的频率从一个跳到另一个，以提供安全的传输。在每个频率跳跃上花费的时间量称为驻留时间。

直接序列扩频 (DSSS)

每当用户想要使用这种DSSS技术发送数据时，用户数据的每个比特都乘以一个秘密代码，称为码片码。此码片码只不过是与原始消息相乘并传输的扩频码。接收器使用相同的代码来检索原始消息。

FHSS和DSSS/CDMA的比较

两种扩频技术都以其特性而闻名。为了更好地理解，让我们来看看它们的比较。

FHSS	DSSS/CDMA
使用多个频率	使用单一频率
很难在任何时刻找到用户的频率	一旦分配，用户频率始终相同
允许频率复用	不允许频率复用
发送器无需等待	如果频谱繁忙，发送器必须等待
信号的功率强度高	信号的功率强度低
更强大，可以穿透障碍物	与FHSS相比较弱
从不受干扰影响	可能会受到干扰影响
更便宜	更昂贵
这是常用的技术	此技术不经常使用

扩频的优点

以下是扩频的优点：

消除串扰
具有数据完整性的更好输出
减少多径衰落的影响
更好的安全性
降低噪声
与其他系统共存
更长的工作距离
难以检测
不容易解调/解码
难以阻塞信号

虽然扩频技术最初是为军事用途而设计的，但现在它们正广泛用于商业目的。

打印页面

数字通信 - 快速指南

数字通信 - 模拟到数字

数字化的必要性

数字通信的优势

数字通信的组成部分

信源

这是一个传感器，它接收物理输入并将其转换为电信号 (**例如**: 麦克风)。此模块还包含一个**模拟到数字**转换器，在需要数字信号进行进一步处理的情况下。

信源编码器

信道编码器

数字调制器

信道

数字解调器

信道解码器

信源解码器

输出传感器

输出信号

脉冲编码调制

PCM 的基本元件

低通滤波器

采样器

量化器

编码器

再生中继器

解码器

重建滤波器

数字通信 - 采样

采样率

奈奎斯特率

采样定理

混叠

傅里叶变换的范围

数字通信 - 量化

模拟信号的量化

量化类型

量化误差

量化噪声

PCM中的压扩

A律压扩技术

μ律压扩技术

数字通信 - 差分脉冲编码调制 (DPCM)

DPCM发射机

DPCM接收机

数字通信 - 增量调制

增量调制

增量调制的特点

增量调制器

增量解调器

增量调制优于差分脉冲编码调制的优点

自适应增量调制 (ADM)

数字通信 - 技术

线性预测编码

多路复用

多路复用器的类型

模拟多路复用

频分多路复用 (FDM)

波分多路复用 (WDM)

数字多路复用

时分多路复用 (TDM)

同步 TDM

异步 TDM

再生中继器

均衡器

定时电路

决策设备

数字通信 - 线路码

线路编码的特性

线路编码的类型

单极性信号

单极性不归零 (NRZ)

单极性归零 (RZ)

双极性信号

双极性NRZ

双极性RZ

双极性信号

优点

缺点

功率谱密度

PSD推导

数据编码技术

数据编码

这是一个传感器，它接收物理输入并将其转换为电信号 (例如: 麦克风)。此模块还包含一个模拟到数字转换器，在需要数字信号进行进一步处理的情况下。