
数字通信 - 差错控制编码
噪声或错误是信号中的主要问题,它会干扰通信系统的可靠性。差错控制编码是用于控制错误发生的编码过程。这些技术有助于错误检测和错误纠正。
根据应用的数学原理,存在许多不同的纠错码。但是,历史上,这些代码已被分为线性分组码和卷积码。
线性分组码
在线性分组码中,奇偶校验位和消息位具有线性组合,这意味着生成的码字是任意两个码字的线性组合。
让我们考虑一些数据块,每个数据块包含k位。这些位与每个数据块包含n位的块映射。这里n大于k。发送器添加冗余位,即(n-k)位。比率k/n是码率。它用r表示,r的值为r < 1。
这里添加的(n-k)位是奇偶校验位。奇偶校验位有助于错误检测和错误纠正,以及定位数据。在传输的数据中,码字的最左边的位对应于消息位,码字的最右边的位对应于奇偶校验位。
系统码
任何线性分组码都可以是系统码,直到它被改变。因此,未更改的分组码称为系统码。
以下是根据其分配的码字结构表示。
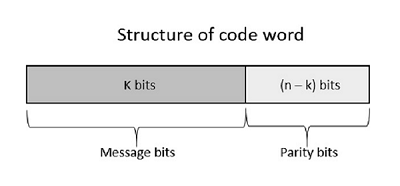
如果消息没有被改变,则称为系统码。这意味着数据的加密不应更改数据。
卷积码
到目前为止,在线性码中,我们已经讨论了首选系统未更改的码。在这里,如果传输总共n位数据,则k位是消息位,(n-k)位是奇偶校验位。
在编码过程中,奇偶校验位从整个数据中减去,并且消息位被编码。现在,奇偶校验位再次被添加,并且整个数据再次被编码。
下图给出了用于信息传输的数据块和数据流的示例。

上述整个过程是繁琐的,存在缺点。当系统繁忙时,缓冲区的分配是一个主要问题。
卷积码消除了此缺点。其中整个数据流被分配符号,然后传输。由于数据是位流,因此无需缓冲区进行存储。
汉明码
码字的线性特性是两个码字的和也是一个码字。汉明码是一种线性纠错码,它可以检测最多两位错误,或者可以纠正一位错误而无需检测未纠正的错误。
使用汉明码时,使用额外的奇偶校验位来识别单比特错误。要从一种比特模式转换到另一种比特模式,需要更改数据中的少量位。此类位的数量可以称为汉明距离。如果奇偶校验的距离为 2,则可以检测到一位翻转。但这无法纠正。此外,任何两位翻转都无法检测到。
然而,汉明码比前面讨论的错误检测和纠正程序更好。
BCH 码
BCH 码以发明者Bose、Chaudari 和Hocquenghem 的名字命名。在 BCH 码设计过程中,可以控制要纠正的符号数量,因此可以进行多比特纠正。BCH 码是纠错码中的一种强大技术。
对于任何正整数m ≥ 3和t < 2m-1,都存在 BCH 二元码。以下是此类代码的参数。
块长度n = 2m-1
奇偶校验位数n - k ≤ mt
最小距离dmin ≥ 2t + 1
此代码可以称为t 错纠正 BCH 码。
循环码
码字的循环特性是码字的任何循环移位也是一个码字。循环码遵循此循环特性。
对于线性码C,如果每个码字,即C = (C1, C2, ...... Cn)来自 C 的分量进行循环右移,则它成为一个码字。此右移等于n-1次循环左移。因此,它在任何移位下都是不变的。因此,线性码C,因为它在任何移位下都是不变的,可以称为循环码。
循环码用于纠错。它们主要用于纠正双重错误和突发错误。
因此,这些是在接收器处要检测的一些纠错码。这些代码可防止错误的引入并干扰通信。它们还可以防止信号被不需要的接收器窃听。有一类信令技术可以实现这一点,这将在下一章中讨论。