
数字通信 - 线路编码
线路编码是在传输线上进行数字信号数据传输时使用的代码。选择此编码过程是为了避免信号重叠和失真,例如符号间干扰。
线路编码的特性
以下是线路编码的特性 -
由于编码是为了在单个信号上传输更多比特,因此使用的带宽大大降低。
对于给定的带宽,功率得到有效利用。
错误概率大大降低。
执行错误检测,并且双极性也具有校正功能。
功率密度更有利。
定时内容充足。
避免长串的1和0以保持透明度。
线路编码的类型
线路编码有 3 种类型
- 单极性
- 极性
- 双极性
单极性信号
单极性信号也称为开关键控或简称OOK。
脉冲的存在表示1,脉冲的不存在表示0。
单极性信号有两种变体 -
- 不归零 (NRZ)
- 归零 (RZ)
单极性不归零 (NRZ)
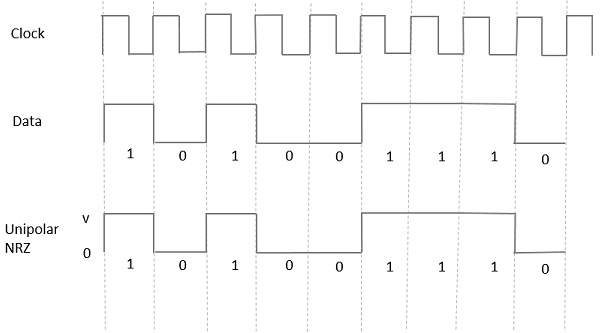
在这种类型的单极性信号中,数据中的高电平由称为标记的正脉冲表示,其持续时间T0等于符号比特持续时间。数据输入中的低电平没有脉冲。
下图清楚地描绘了这一点。
优点
单极性 NRZ 的优点是 -
- 它很简单。
- 需要较少的带宽。
缺点
单极性 NRZ 的缺点是 -
没有执行错误校正。
低频分量的存在可能会导致信号下降。
没有时钟。
可能会发生同步丢失(尤其是在长串的1和0的情况下)。
单极性归零 (RZ)
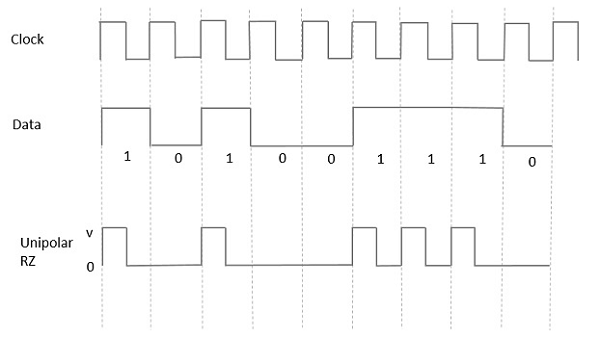
在这种类型的单极性信号中,尽管数据中的高电平由标记脉冲表示,但其持续时间T0小于符号比特持续时间。比特持续时间的一半保持高电平,但它立即返回到零,并在比特持续时间的剩余一半显示脉冲不存在。
借助下图可以清楚地理解这一点。
优点
单极性 RZ 的优点是 -
- 它很简单。
- 位于符号速率处的谱线可用作时钟。
缺点
单极性 RZ 的缺点是 -
- 没有错误校正。
- 占用单极性 NRZ 两倍的带宽。
- 在信号在 0 Hz 处非零的地方会引起信号下降。
极性信号
极性信号有两种方法。他们是 -
- 极性 NRZ
- 极性 RZ
极性 NRZ
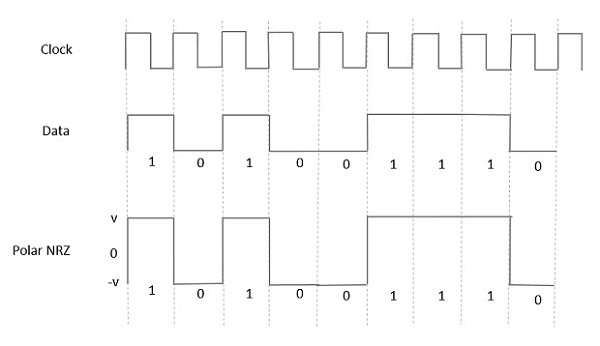
在这种类型的极性信号中,数据中的高电平由正脉冲表示,而数据中的低电平由负脉冲表示。下图很好地描绘了这一点。
优点
极性 NRZ 的优点是 -
- 它很简单。
- 不存在低频分量。
缺点
极性 NRZ 的缺点是 -
没有错误校正。
没有时钟。
在信号在0 Hz处非零的地方会引起信号下降。
极性 RZ
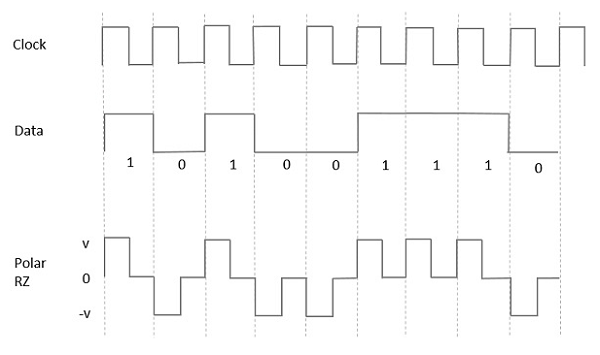
在这种类型的极性信号中,尽管数据中的高电平由标记脉冲表示,但其持续时间T0小于符号比特持续时间。比特持续时间的一半保持高电平,但它立即返回到零,并在比特持续时间的剩余一半显示脉冲不存在。
但是,对于低输入,负脉冲表示数据,零电平在比特持续时间的另一半保持相同。下图清楚地描绘了这一点。
优点
极性 RZ 的优点是 -
- 它很简单。
- 不存在低频分量。
缺点
极性 RZ 的缺点是 -
没有错误校正。
没有时钟。
占用极性 NRZ 两倍的带宽。
在信号在0 Hz处非零的地方会引起信号下降。
双极性信号
这是一种编码技术,它具有三个电压电平,即+、-和0。这种信号称为双二进制信号。
这种类型的一个示例是交替标记反转 (AMI)。对于1,电压电平从 + 变换到 – 或从 – 变换到 +,交替的1具有相同的极性。0将具有零电压电平。
即使在这种方法中,我们也有两种类型。
- 双极性 NRZ
- 双极性 RZ
从迄今为止讨论的模型中,我们了解了 NRZ 和 RZ 之间的区别。它在这里也以同样的方式进行。下图清楚地描绘了这一点。
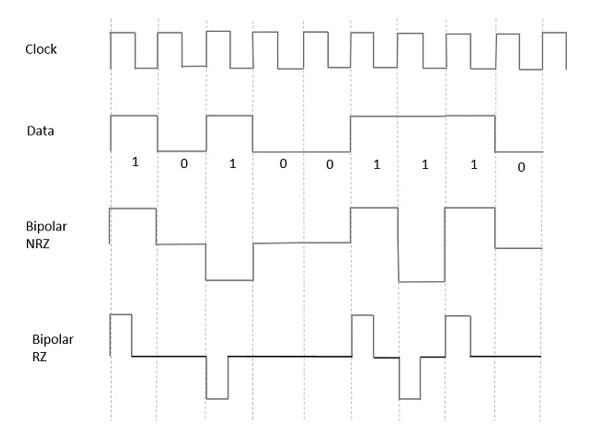
上图同时显示了双极性 NRZ 和 RZ 波形。在 NRZ 类型中,脉冲持续时间和符号比特持续时间相等,而在 RZ 类型中,脉冲持续时间是符号比特持续时间的一半。
优点
以下是优点 -
它很简单。
不存在低频分量。
占用比单极性和极性 NRZ 方案更低的带宽。
此技术适用于通过交流耦合线路传输,因为这里不会发生信号下降。
它具有单错误检测功能。
缺点
以下是缺点 -
- 没有时钟。
- 长串数据会导致同步丢失。
功率谱密度
描述信号功率如何在频域中分布在各个频率上的函数称为功率谱密度 (PSD)。
PSD 是自相关(观测值之间的相似性)的傅里叶变换。它采用矩形脉冲的形式。
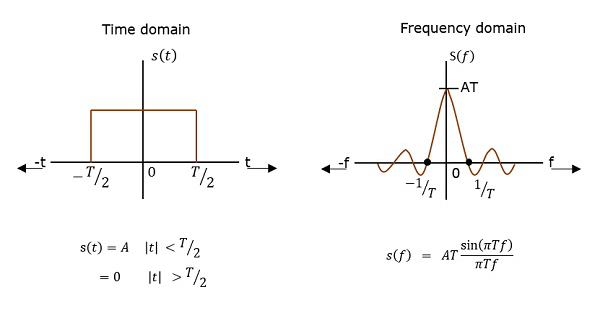
PSD 推导
根据爱因斯坦-维纳-辛钦定理,如果知道随机过程的自相关函数或功率谱密度,则可以精确地找到另一个。
因此,为了推导出功率谱密度,我们将使用功率信号 $x(t)$ 的时间自相关 $(R_x(\tau))$,如下所示。
$R_x(\tau) = \lim_{T_p \rightarrow \infty}\frac{1}{T_p}\int_{\frac{{-T_p}}{2}}^{\frac{T_p}{2}}x(t)x(t + \tau)dt$
由于 $x(t)$ 由脉冲组成,因此 $R_x(\tau)$ 可以写成
$R_x(\tau) = \frac{1}{T}\displaystyle\sum\limits_{n = -\infty}^\infty R_n\delta(\tau - nT)$
其中 $R_n = \lim_{N \rightarrow \infty}\frac{1}{N}\sum_ka_ka_{k + n}$
了解到对于实信号 $R_n = R_{-n}$,我们有
$S_x(w) = \frac{1}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$
由于脉冲滤波器的频谱为 $(w) \leftrightarrow f(t)$,我们有
$s_y(w) = \mid F(w) \mid^2S_x(w)$
$= \frac{\mid F(w) \mid^2}{T}(\displaystyle\sum\limits_{n = -\infty}^\infty R_ne^{-jnwT_{b}})$
$= \frac{\mid F(w) \mid^2}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$
因此,我们得到了功率谱密度的方程。使用它,我们可以找到各种线路编码的 PSD。