信源编码定理

离散无记忆信源产生的代码必须有效地表示，这是通信中一个重要的问题。为此，存在表示这些信源代码的码字。

例如，在电报中，我们使用莫尔斯电码，其中字母由点和划表示。如果考虑使用频率最高的字母E，则用“.”表示，而很少使用的字母Q则用“--.-”表示。

让我们看一下框图。

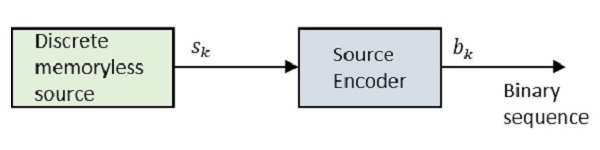
其中S_k是离散无记忆信源的输出，b_k是信源编码器的输出，用0和1表示。

编码序列便于接收端解码。

假设信源的字母表有k个不同的符号，第k个符号S_k出现的概率为P_k，其中k = 0, 1…k-1。

设编码器为符号S_k分配的二进制码字长度为l_k（以比特为单位）。

因此，我们将信源编码器的平均码字长度L定义为

$$\overline{L} = \displaystyle\sum\limits_{k=0}^{k-1} p_kl_k$$

L表示每个信源符号的平均比特数。

如果 $L_{min} = \: \overline{L}的最小可能值$

则编码效率可以定义为

$$\eta = \frac{L_{min}}{\overline{L}}$$

由于$\overline{L}\geq L_{min}$，我们将有$\eta \leq 1$

然而，当$\eta = 1$时，信源编码器被认为是有效的。

为此，必须确定$L_{min}$的值。

让我们参考定义：“给定一个熵为$H(\delta)$的离散无记忆信源，任何信源编码的平均码字长度L都受限于$\overline{L} \geq H(\delta)$。”

简单来说，码字（例如，QUEUE的莫尔斯电码是-.- ..- . ..- .）总是大于或等于信源代码（例如QUEUE）。这意味着码字中的符号大于或等于信源代码中的字母。

因此，当$L_{min} = H(\delta)$时，根据熵$H(\delta)$，信源编码器的效率可以写成

$$\eta = \frac{H(\delta)}{\overline{L}}$$

此信源编码定理称为无噪声编码定理，因为它建立了无错误编码。它也称为香农第一定理。