在一个班级 35 名学生的体检中，记录了他们的体重。

体重（公斤）	学生人数
小于 38	0
小于 40	3
小于 42	5
小于 44	9
小于 46	14
小于 48	28
小于 50	32
小于 52	35

根据给定数据绘制“小于”型累积频率曲线。由此，从图中得到中位体重，并用公式验证结果。

---

已知

在一个班级 35 名学生的体检中，记录了他们的体重。

需要做

我们需要根据给定数据绘制“小于”型累积频率曲线，并从图中得到中位体重，并用公式验证结果。

解答

我们首先根据“小于”方法准备累积频率分布表，如下所示

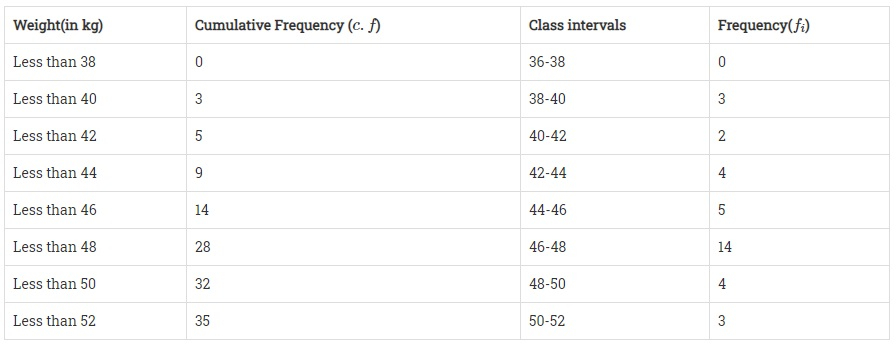
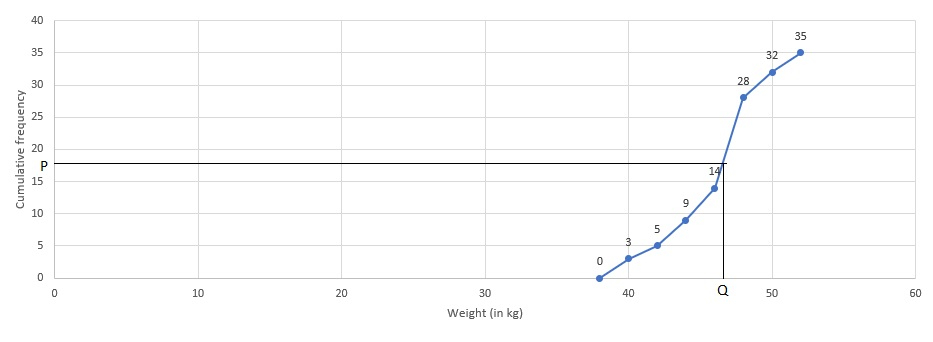
将体重沿 X 轴表示，将累积频率沿 Y 轴表示。

在图上绘制点 (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35)，并用自由手绘线连接它们以得到一条累积频率曲线，如图所示。

这里，

$N = 35$

$\frac{N}{2}=\frac{35}{2}=17.5$

从 Y 轴上的点 $P$ (17.5) 画一条平行于 X 轴的线，与曲线相交，然后画一条平行于 Y 轴的线，与 X 轴在 $Q$ 点相交。

从图中，中位数约为 46.5 公斤。

因此，
46-48 是中位数组
这里，

$l= 46, h = 2,f= 14, F= 14$

这意味着，

中位数 $=l+\frac{\frac{N}{2}-F}{f} \times h$

$=46+\frac{17.5-14}{14} \times 2$

$=46+\frac{3.5 \times 2}{14}$

$=46+0.5$

$=46.5$

因此验证。