数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学导体尺寸的经济选择——开尔文定律（电力传输的经济性）
设计输电线路所需的导体材料成本是输电线路总成本中相当大的一部分。因此，确定输电线路导体的合适尺寸非常重要。输电线路导体的合适尺寸由**开尔文定律**(由开尔文勋爵于1881年提出)确定。
开尔文定律指出，最经济的导体截面积是使输电线路总年成本最低的截面积。
输电线路的总年成本可以分为两部分：
- 资本成本的年度费用
- 导体中能量损耗的年度成本
资本成本的年度费用
这些年度费用是由于输电线路完整安装的资本成本的利息和折旧造成的。对于架空输电系统，完整的安装成本将是导体、电线杆支撑物和绝缘子的资本成本的年度利息和折旧，以及它们的安装成本。
现在，对于架空输电系统，导体的成本与横截面积成正比，绝缘子的成本是恒定的，电线杆（或铁塔）支撑物及其安装成本部分是恒定的，部分与导体的横截面积成正比。
因此，架空输电线路资本成本的年度费用可以表示为：
$$\mathrm{年度费用\mathit{\mathrm{\, =\, } P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\; \; \; \cdot \cdot \cdot \left ( \mathrm{1} \right )}}$$
其中，P1和P2是常数，a是导体的横截面积。
导体中能量损耗的年度成本
此成本是由于导体中I2R损耗引起的能量损耗造成的。假设导体中全年电流恒定，则导体中的功率损耗与电阻成正比。由于导体的电阻与导体的横截面积成反比，因此导体中能量损失与横截面积成反比。
因此，架空输电线路导体中能量损耗的年度成本可以表示为：
$$\mathrm{能量损耗年度成本\mathit{\mathrm{\, =\, }\frac{P_{\mathrm{3}}}{a}\; \; \;\cdot \cdot \cdot \left ( \mathrm{2} \right ) }}$$
其中，P3是常数。
现在，根据公式(1)和(2)，输电线路的总年度成本由下式给出：
$$\mathrm{线路总年度成本,\: \mathit{Y\mathrm{\, =\, }P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\mathrm{\, +\, }\frac{P_{\mathrm{3}}}{a}\; \; \; \cdot \cdot \cdot \left ( \mathrm{3} \right ) }}$$
因此，当Y对变量（即a）的微分等于零时，输电线路的总年度成本将最小，即
$$\mathrm{\mathit{\frac{dY}{da}}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow \frac{d}{da}\left ( P_{\mathrm{1}}\mathrm{\, +\, }aP_{\mathrm{2}}\mathrm{\, +\, }\frac{P_{\mathrm{3}}}{a} \right )}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow \mathrm{0}\mathrm{\, +\, }P_{\mathrm{2}}-\frac{P_{\mathrm{3}}}{a^{\mathrm{2}}}}\mathrm{\, =\, }0}$$
$$\mathrm{\mathit{\Rightarrow aP_{\mathrm{2}}\mathrm{\, =\, }\frac{P_{\mathrm{3}}}{a}}\; \; \; \cdot \cdot \cdot \left ( 4 \right )}$$
即，
$$\mathrm{资本成本年度费用的可变部分\, =\, 能量损耗年度成本}$$
因此，**开尔文定律**也可以表述为：最经济的导体截面积是使资本成本年度费用的可变部分等于导体中能量损耗年度成本的截面积。
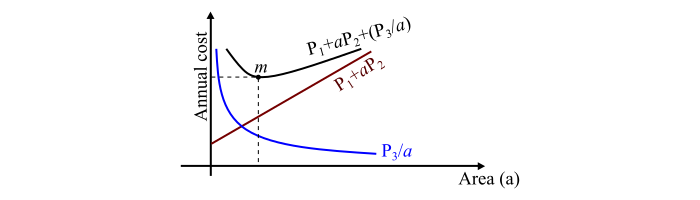
该图显示了开尔文定律的图形表示。这里，m是曲线上最低点，表示最经济的横截面积，即最低的输电线路年度成本。
开尔文定律的局限性
实际上，开尔文定律的局限性如下：
开尔文定律没有考虑几个物理因素，例如安全电流密度、机械强度、电晕损耗等。
由开尔文定律确定的导体尺寸可能并不总是实际可行的，因为它可能太小而无法安全地承载必要的电流。
在没有实际负载曲线的情况下，很难估计输电线路中的能量损失，而这些曲线在估算时是不可用的。
假设由于利息和折旧而产生的资本成本年度费用为𝑃1 + 𝑎𝑃2 的形式，严格来说是不正确的。因此，无法准确确定资本成本的利息和折旧。
9K+ 次浏览
