电通量

---

简介

卡尔·弗里德里希·高斯被广泛认为是有史以来最伟大的数学家之一。有些人认为他是最伟大的。高斯发现了一种思考库仑定律的方法，使我们能够以直接的方式计算电荷分布的电场。虽然高斯并没有发现新的物理定律，但他对库仑定律的重新表述同样重要。在本教程中，我们将描述电通量、电通量的概念、电场的通量、电通量的单位和量纲公式。

为了理解高斯定律，我们必须首先掌握穿过表面的电通量的概念。这是一种计算穿过表面的总电场的方法。

什么是电通量？

电通量以库仑为单位测量，描述了正电荷和负电荷之间相关的力。电通量可以用从正电荷发出并终止于负电荷的通量线来表示。通过电通量来测量发射电力的表面。

电通量的概念

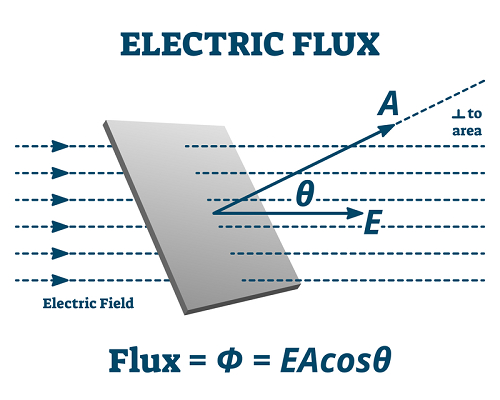
表面用于表示电通量，以及每个点的电场值。为了演示如何确定通量，让我们从一个简单的例子开始。一个恒定的电场（具有相同的矢量值）作用在一个面积为 A 的平面上。

面积矢量 *A* 表征了该表面。这是一个大小为 A 的矢量，垂直于表面。

实际上，这里有一个小问题：就矢量 A 而言，只有两种选择。如果选择这个方向，无论它指向相反的方向，它都将垂直于表面且具有相同的大小。但是，在每个涉及电通量的题目中，选择的方向都是显而易见的。

在这个简单的情况下，电通量 φ 由下式给出：

$$\mathrm{\phi =E.A=EAcos\theta }$$

通常，对于非平坦的表面，可能需要使用高级微积分方法来找到通量，并且电场在该表面上不会是均匀的（大小或方向）。但是，基本思想很简单。如果我们将表面分成足够小的部分（例如，正方形），以便对电场进行合理的表示，那么将表面视为平坦的，并将电场视为连续的，是一个很好的近似值。假设第 i 个正方形的面积为 ΔAi，并且电场接近于 Ei。则小正方形的电通量为：

$$\mathrm{\Delta \phi_{i} =\Delta E_{i}.A_{i}}$$

为了得到整个表面的总电通量，近似等于将所有单个贡献相加。

$$\mathrm{\Delta \phi_{i} \approx\sum_{i}^{} \Delta E_{i}.A_{i}}$$

通过增加小正方形的数量并减小它们的大小，我们可以接近电通量 φ 的真实值。在微积分中，也可以使用类似的过程计算（一个变量的）积分。在这里，我们得到一个曲面积分，并且在表面 S 上的电通量为：

$$\mathrm{\phi =\oint E.dA}$$

电场的通量

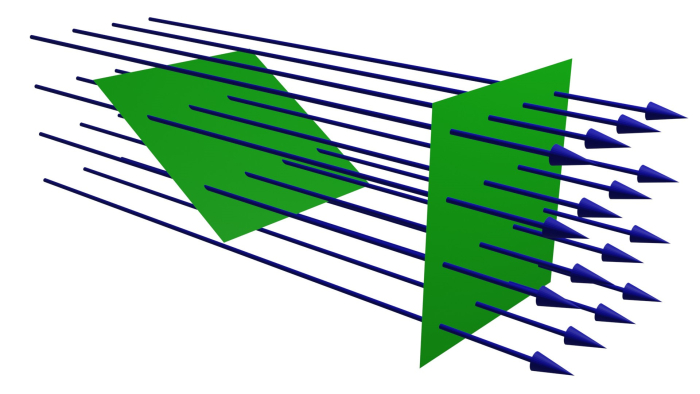
这是一个最简单的例子：电场是恒定的，表面垂直于它。通过将表面积 A 乘以电场强度，计算穿过表面的电通量。

$$\mathrm{\phi = E.A}$$

在这种情况下，通量测量有多少条场线穿过表面。如果表面倾斜一定角度，预计穿过表面的线会更少。如果它平行于这些线，则没有任何东西穿过表面。

定义为穿过其法线与场线成一定角度的表面的通量为：

$$\mathrm{\phi = EAcos\theta }$$

每个表面都有一个与其相关的法线方向。表面的面积可以被认为是一个具有法线方向的矢量。通量是通过取电场和该面积矢量的点积来计算的。

$$\mathrm{\phi = E.A}$$

电场具有一种称为电通量的特性，它是穿过给定面积的力线的数量。假设电场线始于正电荷，终止于负电荷。

指向封闭表面的场线为负，而指向封闭表面外的场线为正。当封闭表面上没有净电荷时，场线穿过其内部，并在其他地方向外指向。当净通量为零时，或者负通量的大小等于正通量的大小时，电通量的大小相等。

电通量的单位和量纲公式

电通量以库仑为单位测量，描述了正电荷和负电荷之间相关的力。电通量可以用从正电荷发出并终止于负电荷的通量线来表示。通过电通量来测量发射电力的表面。

电通量的单位是 \(\mathrm{\frac{牛顿\times 米^{2}}{库仑}}\) 或 \(\mathrm{\frac{Nm^{2}}{c}}\)，量纲是 \(\mathrm{\left [ M^{1}L^{3}T^{-3} I^{-1}\right ]}\)。

结论

电通量取决于穿过电场中给定区域的线数。假设这些线始于正电荷，终止于负电荷。正场线指向封闭表面内部，而负场线指向封闭表面外部。在本教程中，我们描述了电通量、电通量的概念、电场的通量、电通量的单位和量纲公式。

常见问题

Q1. 电通量受距离影响吗？

A1. 通量与距离 r 无关。围绕点电荷的封闭表面将产生相同的结果，无论其大小如何。

Q2. 波的通量是什么意思？

A2. 它是通过垂直于波传播方向的特定区域的能量量。它用 *S* 表示。

Q3. 能有负通量吗？

A3. 请记住，穿过表面的电场线的数量与通量成正比。电场线将进入或离开封闭表面，因此相应的通量将为正或负。

Q4. 电通量的意义是什么？

A4. 电通量的物理意义在处理位移电流的安培-麦克斯韦定律中得到了揭示。需要电通量来解释电容电路中的电流连续性。

Q5. 通量受速度影响吗？

A5. 通量等于垂直于场投影的面积和场的幅度。在这种情况下，只有当平面相对于场的方向改变其方向时，通量才会改变。因此，最终答案是，在这种情况下，通量与速度无关。