遗传算法 - 高级主题

在本节中，我们将介绍遗传算法中的一些高级主题。只想了解遗传算法基础知识的读者可以选择跳过本节。

约束优化问题

约束优化问题是指那些需要在满足某些约束条件下最大化或最小化给定目标函数值的问题。因此，并非解空间中的所有结果都是可行的，解空间包含可行区域，如下图所示。

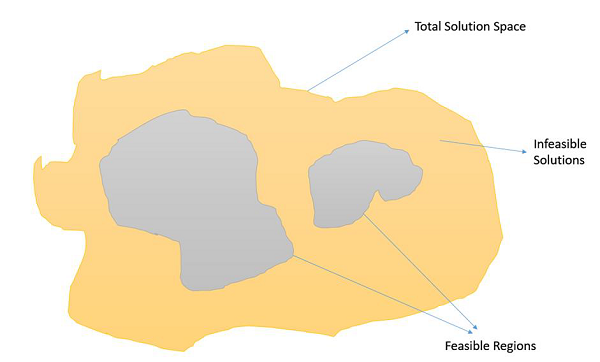
在这种情况下，交叉和变异算子可能会给我们不可行的解。因此，在处理约束优化问题时，必须在遗传算法中采用其他机制。

一些最常用的方法是：

• 使用惩罚函数，降低不可行解的适应度，最好是使适应度随着违反约束的数量或与可行区域的距离成比例地降低。

• 使用修复函数，将不可行解修改为满足违反的约束条件。

• 不允许不可行解进入种群。

• 使用特殊的表示或解码函数，以确保解的可行性。

基本理论背景

在本节中，我们将讨论模式定理和NFL定理以及构建块假设。

模式定理

研究人员一直在试图弄清楚遗传算法工作背后的数学原理，而Holland的模式定理是朝着这个方向迈出的一步。多年来，对模式定理进行了各种改进和建议，使其更具通用性。

在本节中，我们不会深入探讨模式定理的数学原理，而是试图对模式定理是什么有一个基本的理解。需要了解的基本术语如下：

• 模式是一个“模板”。形式上，它是在字母表 = {0,1,*} 上的一个字符串，

  其中*是通配符，可以取任何值。

  因此，*10*1可以表示01001、01011、11001或11011

  几何上，模式是解搜索空间中的超平面。

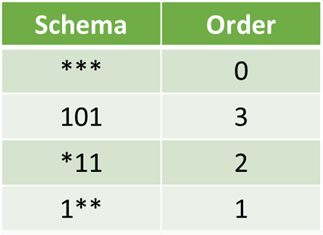
• 模式的阶是基因中指定固定位置的数量。

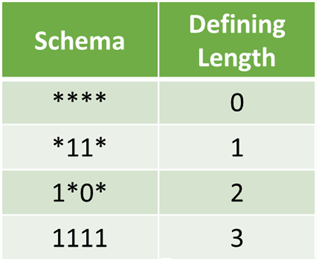
• 定义长度是基因中两个最远固定符号之间的距离。

模式定理指出，具有高于平均适应度、较短定义长度和较低阶的模式更有可能在交叉和变异中存活下来。

构建块假设

构建块是具有高于平均适应度的低阶、低定义长度模式。构建块假设认为，随着遗传算法的进行，通过逐步识别和重新组合这些“构建块”，这些构建块构成了遗传算法成功和适应的基础。

没有免费午餐(NFL)定理

Wolpert和Macready在1997年发表了一篇题为“优化问题的无免费午餐定理”的论文。它本质上指出，如果我们对所有可能问题的空间进行平均，那么所有非重复访问黑盒算法都将表现出相同的性能。

这意味着，我们对问题的了解越多，我们的遗传算法就越针对特定问题，并且性能越好，但它会通过在其他问题上的表现不佳来弥补这一点。

基于遗传算法的机器学习

遗传算法也应用于机器学习。分类器系统是一种经常用于机器学习领域的基于遗传的机器学习(GBML)系统。GBML方法是机器学习的一种利基方法。

GBML系统分为两类：

• 匹兹堡方法——在这种方法中，一个染色体编码一个解，因此适应度分配给解。

• 密歇根方法——一个解通常由多个染色体表示，因此适应度分配给部分解。

需要注意的是，交叉、变异、拉马克式或达尔文式等标准问题也存在于GBML系统中。