遗传算法 - 交叉

本章将讨论交叉算子的含义及其其他模块、用途和优点。

交叉简介

交叉算子类似于生物繁殖和生物交叉。在这种方法中，选择多个父代，并使用父代的遗传物质产生一个或多个子代。交叉通常以高概率应用于遗传算法 – p_c。

交叉算子

本节将讨论一些最常用的交叉算子。需要注意的是，这些交叉算子非常通用，遗传算法设计者也可以选择实现特定问题的交叉算子。

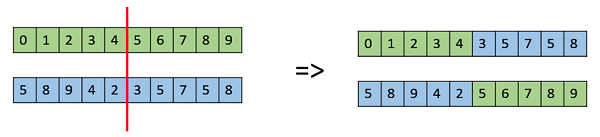
单点交叉

在单点交叉中，选择一个随机交叉点，并将两个父代的尾部交换以获得新的子代。

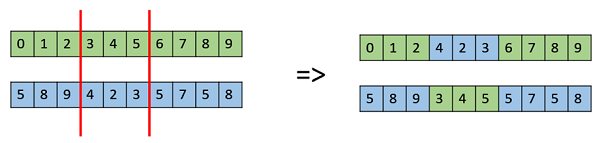
多点交叉

多点交叉是一点交叉的推广，其中交替的片段被交换以获得新的子代。

均匀交叉

在均匀交叉中，我们不将染色体分成片段，而是分别处理每个基因。在这种方法中，我们实际上为每个染色体抛掷一枚硬币，以决定它是否包含在子代中。我们也可以使硬币偏向一个父代，以便子代从该父代获得更多遗传物质。

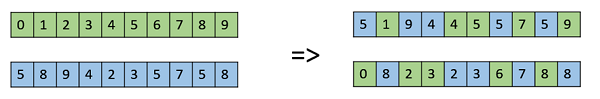
算术重组

这通常用于整数表示，并通过使用以下公式取两个父代的加权平均值来实现：

• 子代1 = α.x + (1-α).y
• 子代2 = α.x + (1-α).y

显然，如果 α = 0.5，则两个子代将相同，如下面的图像所示。

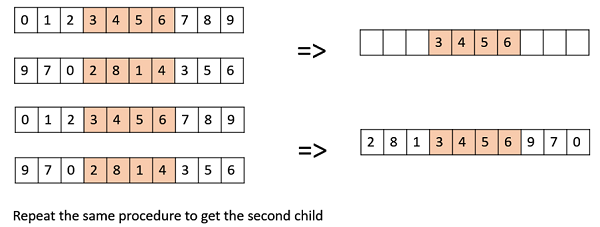
Davis 顺序交叉 (OX1)

OX1 用于基于排列的交叉，目的是将有关相对顺序的信息传递给子代。其工作原理如下：

• 在父代中创建两个随机交叉点，并将第一个父代中它们之间的片段复制到第一个子代。

• 现在，从第二个父代的第二个交叉点开始，将第二个父代中剩余的未使用数字复制到第一个子代，环绕列表。

• 对第二个子代重复此操作，并反转父代的角色。

还存在许多其他交叉，例如部分映射交叉 (PMX)、基于顺序的交叉 (OX2)、洗牌交叉、环交叉等。