遗传算法 - 简介

遗传算法 (GA) 是一种基于遗传和自然选择原理的基于搜索的优化技术。它经常用于寻找难以解决的问题的最优解或近似最优解，否则这些问题需要花费一生才能解决。它经常用于解决优化问题、研究和机器学习。

优化简介

优化是改进某些事物的过程。在任何过程中，我们都有一组输入和一组输出，如下图所示。

优化是指以获得“最佳”输出值的方式查找输入值。 “最佳”的定义因问题而异，但在数学术语中，它指的是通过改变输入参数来最大化或最小化一个或多个目标函数。

所有可能的解或输入可以取的值的集合构成了搜索空间。在这个搜索空间中，存在一个点或一组点给出最优解。优化的目标是在搜索空间中找到该点或点集。

什么是遗传算法？

自然一直是全人类伟大的灵感源泉。遗传算法 (GA) 是基于自然选择和遗传概念的基于搜索的算法。GA 是一个更大的计算分支（称为进化计算）的子集。

GA 由 John Holland 及其在密歇根大学的学生和同事（最著名的是 David E. Goldberg）开发，此后已在各种优化问题上进行了尝试，并取得了高度成功。

在 GA 中，我们有一个给定问题的可能解的池或种群。然后，这些解会经历重组和变异（就像在自然遗传中一样），产生新的子代，并且该过程在各个世代中重复。每个个体（或候选解）都被赋予一个适应度值（基于其目标函数值），并且适应性更强的个体有更高的交配几率并产生更多“适应性更强”的个体。这符合达尔文的“适者生存”理论。

这样，我们就可以在几代人的时间里不断“进化”出更好的个体或解决方案，直到达到停止标准。

遗传算法本质上是足够随机的，但它们比随机局部搜索（我们只尝试各种随机解，跟踪迄今为止最好的解）要好得多，因为它们也利用历史信息。

GA 的优势

GA 具有多种优势，使其广受欢迎。这些包括：

• 不需要任何导数信息（许多现实世界问题可能无法获得）。

• 与传统方法相比，速度更快，效率更高。

• 具有非常好的并行能力。

• 优化连续函数和离散函数以及多目标问题。

• 提供一系列“好的”解决方案，而不仅仅是一个解决方案。

• 总是得到问题的答案，随着时间的推移会越来越好。

• 当搜索空间非常大并且涉及大量参数时非常有用。

GA 的局限性

与任何技术一样，GA 也有一些局限性。这些包括：

• GA 不适用于所有问题，特别是那些简单且可以获得导数信息的问题。

• 适应度值被重复计算，这对于某些问题来说可能是计算量很大的。

• 由于具有随机性，因此无法保证解决方案的最优性或质量。

• 如果实现不当，GA 可能无法收敛到最优解。

GA – 动机

遗传算法能够“足够快”地提供“足够好”的解决方案。这使得遗传算法在解决优化问题方面具有吸引力。需要 GA 的原因如下：

解决难题

在计算机科学中，有一大类问题是NP-Hard 的。这实际上意味着，即使是最强大的计算系统也需要很长时间（甚至数年！）才能解决该问题。在这种情况下，GA 被证明是提供可用的近似最优解的有效工具，并且时间较短。

基于梯度的方法的失败

传统的基于微积分的方法的工作原理是从一个随机点开始，并沿梯度的方向移动，直到我们到达山顶。这种技术效率很高，并且非常适用于单峰目标函数，例如线性回归中的成本函数。但是，在大多数现实世界的情况下，我们有一个非常复杂的问题，称为景观，它由许多山峰和许多山谷组成，这会导致此类方法失败，因为它们具有固有的倾向于停留在局部最优值，如下图所示。

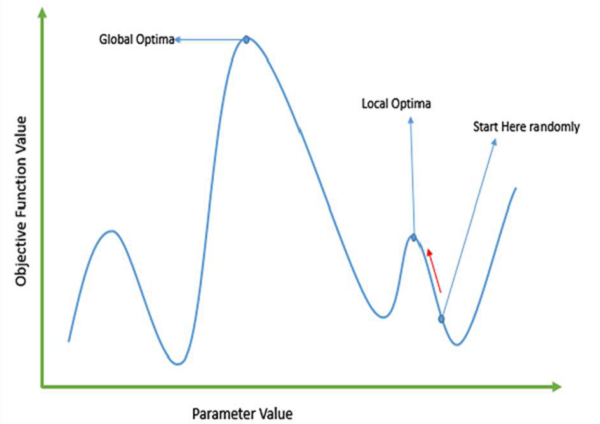
快速获得良好的解决方案

旅行商问题 (TSP) 等一些难题具有现实世界的应用，例如路径查找和 VLSI 设计。现在假设您正在使用 GPS 导航系统，并且它需要几分钟（甚至几小时）才能计算出从起点到目的地的“最佳”路径。在现实世界的应用中，这种延迟是不可接受的，因此需要“足够好”的解决方案，并且“快速”交付。