
- 遗传算法教程
- 遗传算法 – 首页
- 遗传算法 – 简介
- 遗传算法 – 基础
- 基因型表示
- 遗传算法 – 种群
- 遗传算法 – 适应度函数
- 遗传算法 - 亲本选择
- 遗传算法 – 交叉
- 遗传算法 – 变异
- 幸存者选择
- 终止条件
- 终身适应模型
- 有效实施
- 高级主题
- 应用领域
- 进一步阅读
- 遗传算法资源
- 遗传算法 - 快速指南
- 遗传算法 - 资源
- 遗传算法 - 讨论
遗传算法 - 亲本选择
亲本选择是选择进行交配并重组以创建下一代后代的父母的过程。亲本选择对于 GA 的收敛速度至关重要,因为优秀的父母会将个体引导到更好、更适合的解决方案。
但是,应注意防止一个极其适合的解决方案在几代人中接管整个种群,因为这会导致解决方案在解决方案空间中彼此靠近,从而导致多样性丧失。保持良好的多样性对于 GA 的成功至关重要。一个极其适合的解决方案接管整个种群的情况称为过早收敛,这是 GA 中不希望出现的情况。
适应度比例选择
适应度比例选择是最流行的亲本选择方法之一。在这种方法中,每个个体成为父母的概率与其适应度成正比。因此,适应度更高的个体具有更高的交配机会,并将它们的特征传播到下一代。因此,这种选择策略对种群中适应度更高的个体施加选择压力,随着时间的推移逐渐进化出更优秀的个体。
考虑一个圆形轮子。该轮子被分成n 个扇形,其中 n 是种群中个体的数量。每个个体获得圆形的一部分,这部分与其适应度值成正比。
适应度比例选择有两种实现方式:
轮盘赌选择
在轮盘赌选择中,圆形轮子如前所述进行划分。在轮子圆周上选择一个固定点,如图所示,然后旋转轮子。轮子前面出现的区域被选为亲本。对于第二个亲本,重复相同的过程。
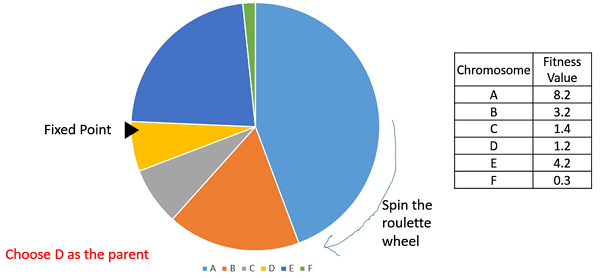
很明显,适应度更高的个体在轮子上拥有更大的扇形,因此当轮子旋转时,它更有可能落在固定点前面。因此,选择个体的概率直接取决于其适应度。
从实现的角度来看,我们使用以下步骤:
计算 S = 适应度的总和。
生成一个介于 0 和 S 之间的随机数。
从种群的顶部开始,不断将适应度添加到部分和 P 中,直到 P<S。
P 超过 S 的个体是被选中的个体。
随机通用抽样 (SUS)
随机通用抽样与轮盘赌选择非常相似,但是,它不是只有一个固定点,而是有多个固定点,如以下图像所示。因此,所有父母都在一次旋转轮子中被选中。此外,这种设置鼓励高度适应的个体至少被选中一次。
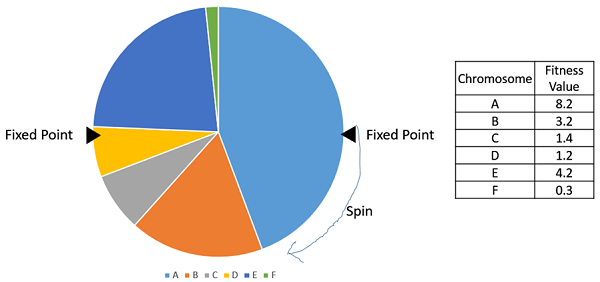
需要注意的是,适应度比例选择方法不适用于适应度可以取负值的情况。
锦标赛选择
在 K 路锦标赛选择中,我们从种群中随机选择 K 个个体,并选择其中最好的个体作为亲本。重复相同的过程以选择下一个亲本。锦标赛选择在文献中也极其流行,因为它甚至可以处理负适应度值。
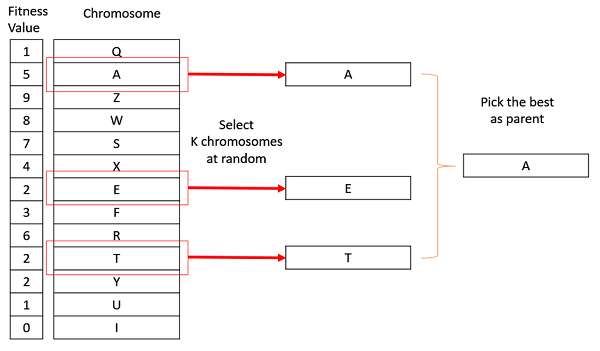
等级选择
等级选择也适用于负适应度值,并且主要用于种群中个体具有非常接近的适应度值的情况(这通常发生在运行结束时)。这导致每个个体几乎拥有相同的扇形比例(如适应度比例选择的情况),因此每个个体无论其相对适应度如何,都具有大致相同的被选为亲本的概率。这反过来会导致对适应度更高个体的选择压力降低,导致 GA 在此类情况下做出糟糕的亲本选择。
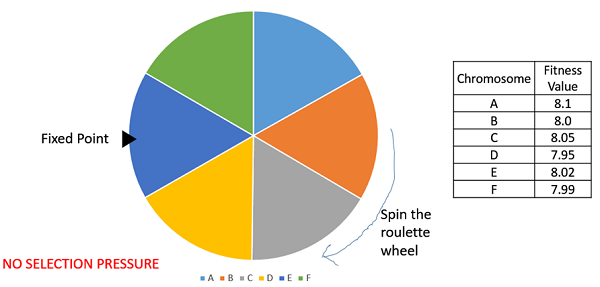
在这种方法中,我们在选择亲本时去除了适应度值的概念。但是,种群中的每个个体都根据其适应度进行排名。亲本的选择取决于每个个体的排名,而不是适应度。排名更高的个体比排名较低的个体更受欢迎。
| 染色体 | 适应度值 | 等级 |
|---|---|---|
| A | 8.1 | 1 |
| B | 8.0 | 4 |
| C | 8.05 | 2 |
| D | 7.95 | 6 |
| E | 8.02 | 3 |
| F | 7.99 | 5 |
随机选择
在这种策略中,我们从现有种群中随机选择亲本。对适应度更高的个体没有选择压力,因此通常避免使用这种策略。