遗传算法 - 快速指南

遗传算法 - 简介

遗传算法 (GA) 是一种基于遗传和自然选择原理的搜索优化技术。它常用于寻找复杂问题的最优或近似最优解，而这些问题如果用其他方法解决可能需要花费很长时间。它常用于解决优化问题、科研和机器学习。

优化简介

优化是指使某件事物变得更好的过程。在任何过程中，我们都有一组输入和一组输出，如下图所示。

优化是指以这样的方式找到输入的值，以便我们获得“最佳”输出值。“最佳”的定义因问题而异，但在数学术语中，它指的是通过改变输入参数来最大化或最小化一个或多个目标函数。

所有可能的解或输入可以取的值的集合构成了搜索空间。在这个搜索空间中，存在一个点或一组点，它给出了最优解。优化的目的是在搜索空间中找到该点或点集。

什么是遗传算法？

大自然一直是全人类灵感的重要来源。遗传算法 (GA) 是基于自然选择和遗传概念的基于搜索的算法。GA 是一个更大计算分支（称为进化计算）的一个子集。

GA 由 John Holland 及其在密歇根大学的学生和同事（最著名的是 David E. Goldberg）开发，并且此后已在各种优化问题上进行了尝试，取得了高度成功。

在 GA 中，我们有一个给定问题的可能解的池或种群。然后，这些解经历重组和变异（就像在自然遗传中一样），产生新的后代，并且该过程在各个世代中重复。每个个体（或候选解）都被分配一个适应度值（基于其目标函数值），并且适应性强的个体更有机会交配并产生更多“适应性强”的个体。这与达尔文的“适者生存”理论一致。

这样，我们就可以在几代人中不断“进化”出更好的个体或解决方案，直到我们达到停止标准。

遗传算法本质上是随机的，但它们比随机局部搜索（我们只是尝试各种随机解决方案，并跟踪迄今为止最好的解决方案）的性能要好得多，因为它们也利用历史信息。

GA 的优点

GA 具有多种优点，使其广受欢迎。这些包括 -

不需要任何导数信息（对于许多现实世界的问题，这些信息可能不可用）。
与传统方法相比，速度更快、效率更高。
具有非常好的并行能力。
优化连续和离散函数以及多目标问题。
提供一系列“好的”解决方案，而不仅仅是一个解决方案。
始终可以得到问题的答案，并且随着时间的推移会变得更好。
当搜索空间非常大并且涉及大量参数时非常有用。

GA 的局限性

与任何技术一样，GA 也存在一些局限性。这些包括 -

GA 不适合所有问题，特别是那些简单且可以使用导数信息的问题。
适应度值的计算会重复进行，这对于某些问题来说可能是计算量很大的。
由于是随机的，因此无法保证解决方案的最优性或质量。
如果实施不当，GA 可能不会收敛到最优解。

GA – 动机

遗传算法能够以“足够快”的速度提供“足够好”的解决方案。这使得遗传算法在解决优化问题方面极具吸引力。GA 需求的原因如下 -

解决难题

在计算机科学中，有一大类问题是NP-Hard。这实质上意味着，即使是最强大的计算系统也需要很长时间（甚至几年！）才能解决该问题。在这种情况下，GA 被证明是提供可用的近似最优解的有效工具，并且可以在短时间内完成。

基于梯度的方法的失败

传统的基于微积分的方法的工作原理是从一个随机点开始，并沿着梯度的方向移动，直到我们到达山顶。这种技术效率很高，并且非常适用于单峰目标函数（例如线性回归中的成本函数）。但是，在大多数现实世界的情况下，我们有一个非常复杂的问题，称为景观，它由许多山峰和许多山谷组成，这会导致此类方法失败，因为它们存在固有的倾向，即陷入局部最优，如下图所示。

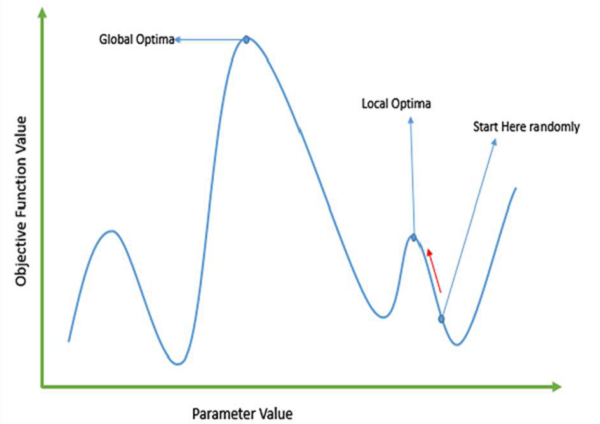
快速获得良好的解决方案

一些难题，如旅行商问题 (TSP)，具有现实世界的应用，如路径查找和 VLSI 设计。现在假设您正在使用 GPS 导航系统，并且它需要几分钟（甚至几小时）才能计算出从源到目的地的“最优”路径。在这样的实际应用中，延迟是不可接受的，因此需要“足够好”的解决方案，并且需要“快速”交付。

遗传算法 - 基础知识

本节介绍理解 GA 所需的基本术语。此外，还以伪代码和图形形式展示了 GA 的通用结构。建议读者充分理解本节中介绍的所有概念，并在阅读本教程的其他部分时牢记这些概念。

基本术语

在开始讨论遗传算法之前，必须熟悉一些基本术语，这些术语将在本教程中使用。

种群 - 它是给定问题所有可能的（编码）解的一个子集。GA 的种群类似于人类的种群，只是我们用代表人类的候选解代替了人类。
染色体 - 染色体是给定问题的一个解。
基因 - 基因是染色体的一个元素位置。
等位基因 - 它是一个特定染色体基因所取的值。

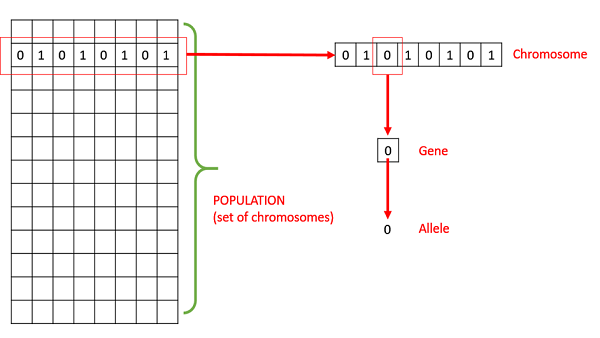
基因型 - 基因型是计算空间中的种群。在计算空间中，解以一种易于理解和使用计算系统进行操作的方式表示。
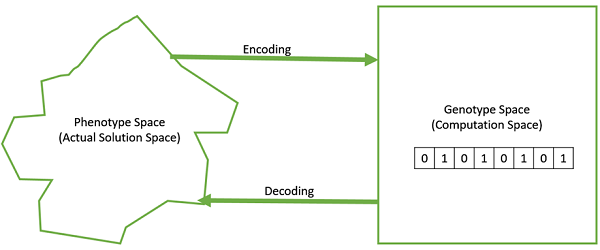
表现型 - 表现型是实际现实世界解空间中的种群，其中解以它们在现实世界中表示的方式表示。
解码和编码 - 对于简单问题，表现型和基因型空间是相同的。但是，在大多数情况下，表现型和基因型空间是不同的。解码是从基因型到表现型空间转换解的过程，而编码是从表现型到基因型空间转换的过程。解码应该很快，因为它在 GA 中在适应度值计算期间会重复进行。

例如，考虑 0/1 背包问题。表现型空间包含仅包含要选择的项目的项目编号的解决方案。

但是，在基因型空间中，它可以表示为长度为 n 的二进制字符串（其中 n 是项目的数量）。位置 x 处的 0 表示第 x 个项目被选中，而 1 表示相反。这是一种基因型和表现型空间不同的情况。

适应度函数 - 简单定义的适应度函数是一个函数，它以解作为输入，并产生解的适用性作为输出。在某些情况下，适应度函数和目标函数可能相同，而在其他情况下，它可能因问题而异。
遗传算子 - 它们改变后代的遗传组成。这些包括交叉、变异、选择等。

基本结构

GA 的基本结构如下 -

我们从一个初始种群开始（可以随机生成或由其他启发式算法播种），从该种群中选择父母进行交配。对父母应用交叉和变异算子以生成新的后代。最后，这些后代替换种群中的现有个体，并且该过程重复。这样，遗传算法实际上在一定程度上试图模仿人类进化。

以下每个步骤将在本教程的后面章节中单独介绍。

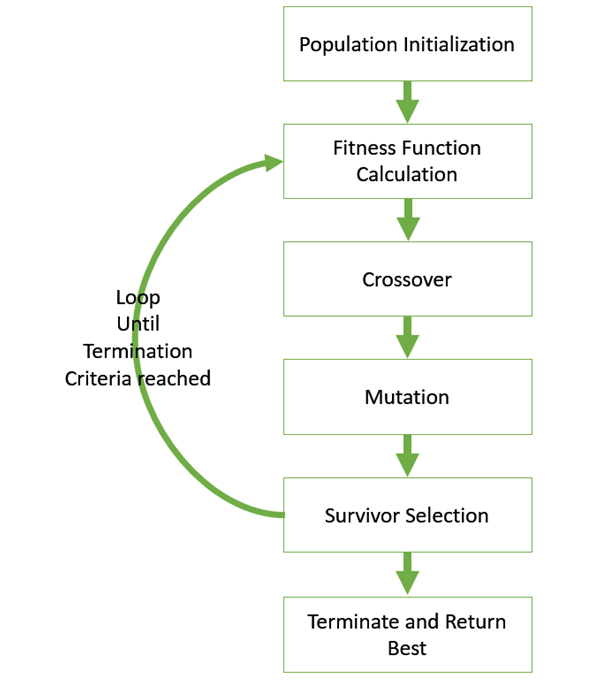
以下程序解释了 GA 的通用伪代码 -

GA()
   initialize population
   find fitness of population
   
   while (termination criteria is reached) do
      parent selection
      crossover with probability pc
      mutation with probability pm
      decode and fitness calculation
      survivor selection
      find best
   return best

基因型表示

在实现遗传算法时，最重要的决定之一是决定我们将用于表示解决方案的表示形式。据观察，不正确的表示会导致 GA 性能下降。

因此，选择合适的表示方法，并对表型和基因型空间之间的映射进行恰当的定义，对于遗传算法的成功至关重要。

在本节中，我们将介绍一些遗传算法中最常用的表示方法。但是，表示方法高度依赖于具体问题，读者可能会发现其他表示方法或此处提到的表示方法的组合可能更适合他的问题。

二进制表示

这是遗传算法中最简单和最广泛使用的表示方法之一。在这种表示方法中，基因型由位串组成。

对于某些问题，当解空间由布尔决策变量（是或否）组成时，二进制表示是自然的。例如，考虑0/1背包问题。如果有n个物品，我们可以用一个n个元素的二进制字符串来表示一个解，其中第x个元素表示是否选择物品x（1）或不选择（0）。

对于其他问题，特别是那些处理数字的问题，我们可以用它们的二进制表示来表示这些数字。这种编码的问题在于不同的位具有不同的意义，因此变异和交叉算子可能产生不希望的结果。这可以通过使用**格雷码**在一定程度上解决，因为一位的变化不会对解产生重大影响。

实值表示

对于我们希望使用连续变量而不是离散变量来定义基因的问题，实值表示是最自然的。然而，这些实值或浮点数的精度受限于计算机。

整数表示

对于离散值基因，我们不能总是将解空间限制为二进制的“是”或“否”。例如，如果我们想编码四个方向——北、南、东和西，我们可以将它们编码为**{0,1,2,3}**。在这种情况下，整数表示是可取的。

排列表示

在许多问题中，解由元素的顺序表示。在这种情况下，排列表示是最合适的。

这种表示法的经典示例是旅行商问题（TSP）。在这种问题中，旅行商必须对所有城市进行巡回，每个城市恰好访问一次，并返回到起始城市。巡回的总距离必须最小化。TSP的解自然地是所有城市的排序或排列，因此对这个问题使用排列表示是有意义的。

遗传算法 - 种群

种群是当前代中解的一个子集。它也可以定义为一组染色体。在处理遗传算法种群时，需要牢记以下几点：

应保持种群的多样性，否则可能会导致过早收敛。
种群规模不应过大，因为它会导致遗传算法速度变慢，而较小的种群可能不足以形成良好的交配池。因此，需要通过反复试验来确定最佳种群规模。

种群通常定义为一个二维数组——**种群规模，染色体长度，基因长度**。

种群初始化

在遗传算法中初始化种群主要有两种方法：

**随机初始化**——用完全随机的解填充初始种群。
**启发式初始化**——使用已知的启发式方法填充初始种群。

观察发现，不应该使用启发式方法初始化整个种群，因为它会导致种群具有相似的解并且多样性很小。实验观察表明，随机解是推动种群达到最优性的因素。因此，对于启发式初始化，我们只用几个好的解来填充种群，其余的用随机解填充，而不是用基于启发式的解填充整个种群。

还观察到，在某些情况下，启发式初始化只会影响种群的初始适应度，但最终，导致最优性的是解的多样性。

种群模型

两种广泛使用的种群模型：

稳态

在稳态遗传算法中，我们在每次迭代中生成一个或两个后代，并用它们替换种群中的一个或两个个体。稳态遗传算法也称为**增量遗传算法**。

代际

在代际模型中，我们生成'n'个后代，其中n是种群规模，并在迭代结束时用新种群替换整个种群。

遗传算法 - 适应度函数

简单来说，适应度函数是一个函数，它**以问题的候选解作为输入，并输出**该解相对于所考虑问题的“适应度”或“优劣”。

在遗传算法中，适应度值的计算会反复进行，因此它应该足够快。适应度值的缓慢计算会对遗传算法产生不利影响，使其异常缓慢。

在大多数情况下，适应度函数和目标函数相同，因为目标是最大化或最小化给定的目标函数。但是，对于具有多个目标和约束的更复杂的问题，**算法设计者**可能会选择使用不同的适应度函数。

适应度函数应具有以下特征：

适应度函数的计算速度应足够快。
它必须定量地衡量给定解的适应度或从给定解可以产生多适应的个体。

在某些情况下，由于手头问题的固有复杂性，可能无法直接计算适应度函数。在这种情况下，我们会进行适应度近似以满足我们的需求。

下图显示了0/1背包问题解的适应度计算。这是一个简单的适应度函数，它只将被选择的物品（值为1）的利润值加起来，从左到右扫描元素，直到背包装满。

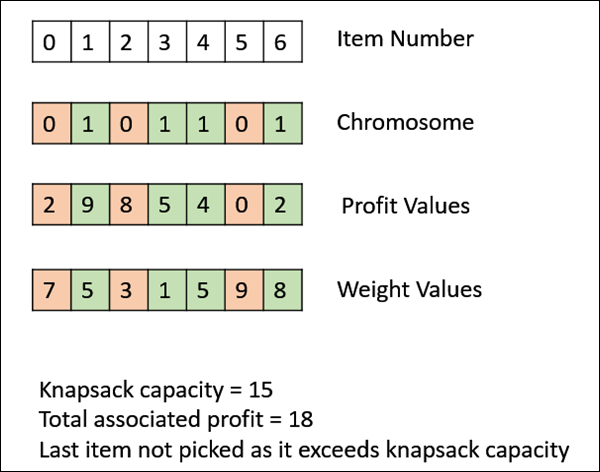
遗传算法 - 亲本选择

亲本选择是选择交配并重组以创建下一代后代的亲本的过程。亲本选择对遗传算法的收敛速度至关重要，因为好的亲本会将个体引导到更好、更适应的解。

但是，应注意防止一个极其适应的解在几代中接管整个种群，因为这会导致解在解空间中彼此靠近，从而导致多样性丧失。**保持种群良好的多样性**对于遗传算法的成功至关重要。一个极其适应的解接管整个种群的情况称为**过早收敛**，这是遗传算法中不希望出现的情况。

适应度比例选择

适应度比例选择是最流行的亲本选择方法之一。在这种方法中，每个个体成为亲本的概率与其适应度成正比。因此，适应性强的个体有更高的机会交配并将它们的特征传播到下一代。因此，这种选择策略对种群中适应性强的个体施加选择压力，随着时间的推移进化出更好的个体。

考虑一个圆形轮盘。轮盘被分成**n块**，其中n是种群中个体的数量。每个个体获得圆形轮盘的一部分，这部分与它的适应度值成正比。

适应度比例选择有两种可能的实现方式：

轮盘赌选择

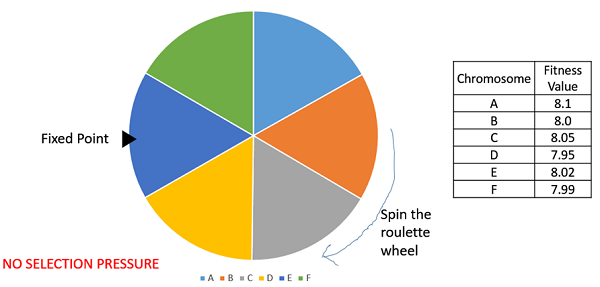
在轮盘赌选择中，圆形轮盘如前所述进行划分。在轮盘圆周上选择一个固定点，如图所示，并旋转轮盘。轮盘中位于固定点前面的区域被选为亲本。对于第二个亲本，重复相同的过程。

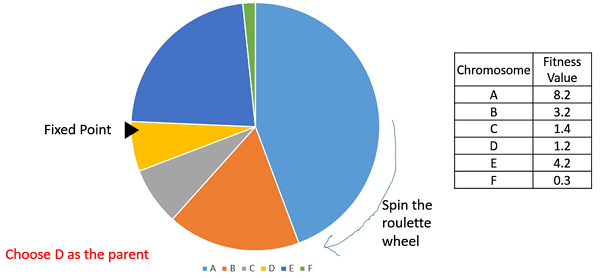
很明显，适应性强的个体在轮盘上占据更大的扇形区域，因此在轮盘旋转时落到固定点前面的概率更大。因此，选择个体的概率直接取决于其适应度。

在实现方面，我们使用以下步骤：

计算S = 适应度之和。
生成一个介于0和S之间的随机数。
从种群的顶部开始，将适应度不断添加到部分和P中，直到P
P超过S的个体是被选择的个体。

随机均匀抽样（SUS）

随机均匀抽样与轮盘赌选择非常相似，但是，我们不是只有一个固定点，而是有多个固定点，如下面的图片所示。因此，所有亲本都在轮盘的一次旋转中被选中。此外，这种设置鼓励高度适应的个体至少被选中一次。

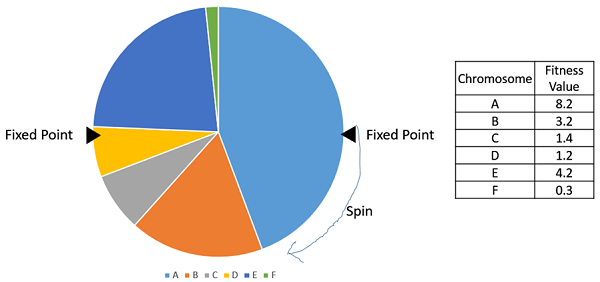
需要注意的是，适应度比例选择方法不适用于适应度可以取负值的情况。

锦标赛选择

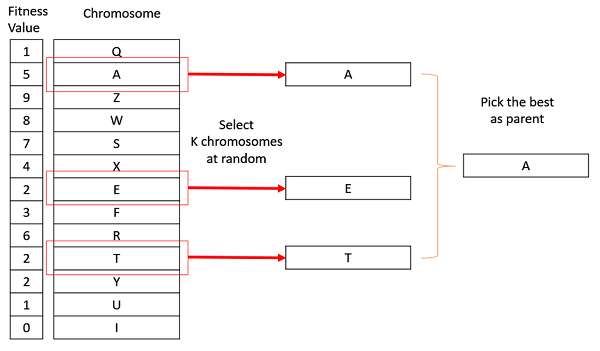
在K路锦标赛选择中，我们从种群中随机选择K个个体，并从中选择最好的个体作为亲本。重复相同的过程以选择下一个亲本。锦标赛选择在文献中也非常流行，因为它甚至可以处理负适应度值。

等级选择

等级选择也可以处理负适应度值，并且主要用于种群中个体具有非常接近的适应度值的情况（通常发生在运行结束时）。这导致每个个体几乎拥有相同比例的扇形区域（如适应度比例选择的情况），因此每个个体无论其相对适应度如何，都具有大致相同的被选为亲本的概率。这反过来会导致对适应性强的个体的选择压力减弱，使遗传算法在这种情况下进行较差的亲本选择。

在这种方法中，我们在选择亲本时去除了适应度值的概念。但是，种群中的每个个体都根据其适应度进行排序。亲本的选择取决于每个个体的等级，而不是适应度。等级较高的个体比等级较低的个体更受青睐。

染色体	适应度值	等级
A	8.1	1
B	8.0	4
C	8.05	2
D	7.95	6
E	8.02	3
F	7.99	5

随机选择

在本策略中，我们从现有种群中随机选择父母。没有针对更适应个体的选择压力，因此通常避免使用此策略。

遗传算法 - 交叉

在本章中，我们将讨论交叉算子及其其他模块、用途和益处。

交叉介绍

交叉算子类似于生物繁殖和生物交叉。在这种情况下，选择多个父母，并使用父母的遗传物质产生一个或多个后代。交叉通常以高概率应用于遗传算法 – p_c 。

交叉算子

在本节中，我们将讨论一些最常用的交叉算子。需要注意的是，这些交叉算子非常通用，遗传算法设计者也可以选择实现特定于问题的交叉算子。

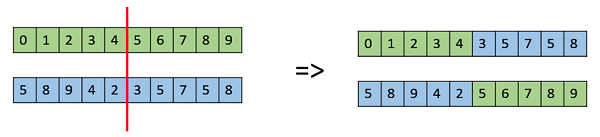
单点交叉

在这种单点交叉中，选择一个随机的交叉点，并交换其两个父代的尾部以获得新的后代。

多点交叉

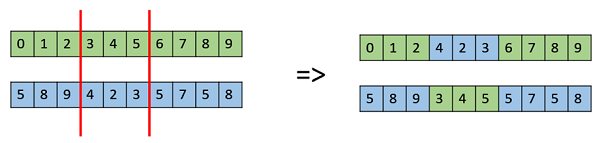
多点交叉是单点交叉的推广，其中交替片段被交换以获得新的后代。

均匀交叉

在均匀交叉中，我们不将染色体分成片段，而是单独处理每个基因。在这种情况下，我们实际上为每个染色体抛硬币，以决定它是否包含在后代中。我们还可以偏向一个父代，使孩子从该父代那里获得更多的遗传物质。

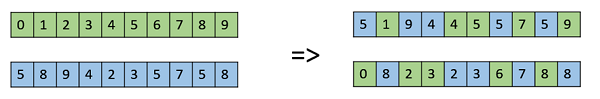
整体算术重组

这通常用于整数表示，并通过使用以下公式取两个父代的加权平均值来工作：

子代1 = α.x + (1-α).y
子代2 = α.x + (1-α).y

显然，如果 α = 0.5，则两个子代将完全相同，如下面的图像所示。

Davis'顺序交叉 (OX1)

OX1 用于基于排列的交叉，目的是将有关相对顺序的信息传递给后代。其工作原理如下：

在父代中创建两个随机交叉点，并将它们之间的片段从第一个父代复制到第一个后代。
现在，从第二个父代的第二个交叉点开始，将第二个父代中剩余的未使用数字复制到第一个子代，环绕列表。
对第二个子代重复此操作，并交换父代的角色。

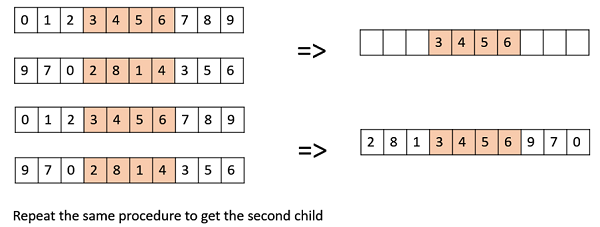
还存在许多其他交叉，例如部分映射交叉 (PMX)、基于顺序的交叉 (OX2)、洗牌交叉、环交叉等。

遗传算法 - 变异

变异介绍

简单来说，变异可以定义为染色体中一个小的随机调整，以获得新的解。它用于维持和引入遗传种群的多样性，并且通常以低概率应用 – p_m。如果概率非常高，则遗传算法会简化为随机搜索。

变异是遗传算法中与搜索空间“探索”相关的一部分。据观察，变异对于遗传算法的收敛至关重要，而交叉则不然。

变异算子

在本节中，我们将描述一些最常用的变异算子。与交叉算子一样，这不是一个详尽的列表，遗传算法设计者可能会发现这些方法的组合或特定于问题的变异算子更有用。

位翻转变异

在这种位翻转变异中，我们选择一个或多个随机位并将其翻转。这用于二进制编码的遗传算法。

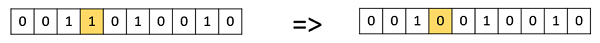
随机重置

随机重置是位翻转对于整数表示的扩展。在这种情况下，从允许值的集合中随机选择一个值并将其分配给随机选择的基因。

交换变异

在交换变异中，我们随机选择染色体上的两个位置，并交换其值。这在基于排列的编码中很常见。

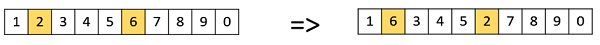
扰乱变异

扰乱变异在基于排列的表示中也很流行。在这种情况下，从整个染色体中选择一个基因子集，并随机扰乱或洗牌其值。

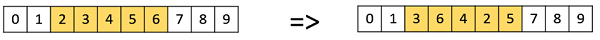
倒位变异

在倒位变异中，我们像在扰乱变异中一样选择一个基因子集，但不是洗牌子集，而只是反转子集中的整个字符串。

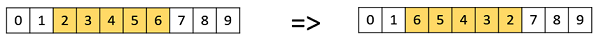
遗传算法 - 幸存者选择

幸存者选择策略决定哪些个体将被淘汰，哪些个体将在下一代中保留。它至关重要，因为它应该确保更适应的个体不会被淘汰出种群，同时也要在种群中保持多样性。

一些遗传算法采用精英策略。简单来说，这意味着种群中当前最适应的成员总是被传播到下一代。因此，在任何情况下，当前种群中最适应的成员都不能被替换。

最简单的策略是将种群中的随机成员淘汰，但这种方法经常存在收敛问题，因此广泛使用以下策略。

基于年龄的选择

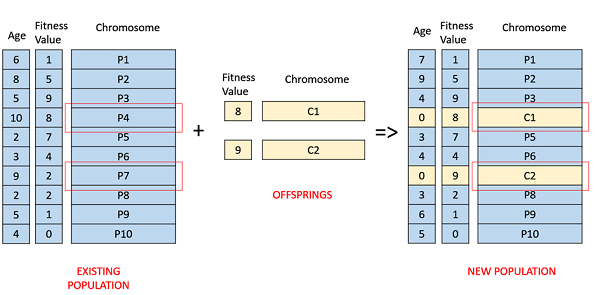
在基于年龄的选择中，我们没有适应度的概念。它基于这样一个前提：每个个体都被允许在种群中存在有限的世代，在此期间它可以繁殖，之后，它将被淘汰出种群，无论其适应度有多好。

例如，在下面的示例中，年龄是个体在种群中存在的世代数。种群中最老的成员，即 P4 和 P7，被淘汰出种群，其余成员的年龄增加 1。

基于适应度的选择

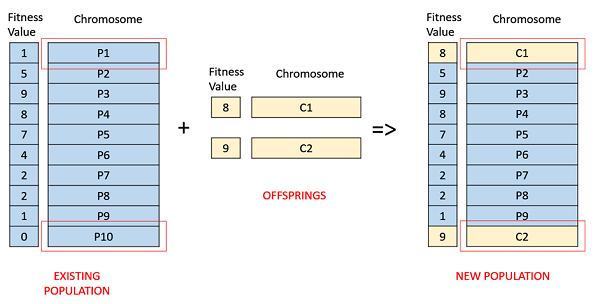
在这种基于适应度的选择中，子代倾向于替换种群中最不适应的个体。最不适应个体的选择可以使用前面描述的任何选择策略的变体完成 - 锦标赛选择、适应度比例选择等。

例如，在下面的图像中，子代替换了种群中最不适应的个体 P1 和 P10。需要注意的是，由于 P1 和 P9 的适应度值相同，因此决定从种群中删除哪个个体是任意的。

遗传算法 - 终止条件

遗传算法的终止条件对于确定遗传算法运行何时结束非常重要。据观察，最初，遗传算法进展非常快，每隔几个迭代就会出现更好的解，但这在后期往往会趋于饱和，改进非常小。我们通常希望终止条件使得我们的解在运行结束时接近最优解。

通常，我们会保留以下终止条件之一：

当种群在 X 次迭代中没有改进时。
当我们达到绝对的世代数时。
当目标函数值达到某个预定义值时。

例如，在遗传算法中，我们保留一个计数器，跟踪种群没有改进的世代数。最初，我们将此计数器设置为零。每次我们没有生成比种群中个体更好的后代时，我们都会增加计数器。

但是，如果任何后代的适应度更好，那么我们将计数器重置为零。当计数器达到预定值时，算法终止。

与遗传算法的其他参数一样，终止条件也高度特定于问题，遗传算法设计者应该尝试各种选项，以了解哪种选项最适合其特定问题。

终身适应模型

到目前为止，在本教程中，我们讨论的内容都对应于达尔文进化模型 - 自然选择以及通过重组和变异产生的遗传变异。在自然界中，只有个体基因型中包含的信息可以传递给下一代。这是我们迄今为止在教程中一直在遵循的方法。

然而，也存在其他终生适应模型 - 拉马克模型和鲍尔德温模型。需要注意的是，哪种模型最好，存在争议，研究人员获得的结果表明，终生适应的选择高度特定于问题。

通常，我们会将遗传算法与局部搜索混合 - 例如在模因算法中。在这种情况下，人们可能会选择使用拉马克模型或鲍尔德温模型来决定对局部搜索后生成的个体进行什么操作。

拉马克模型

拉马克模型本质上说的是，个体在其一生中获得的特征可以遗传给其后代。它以法国生物学家让-巴蒂斯特·拉马克命名。

尽管自然生物学完全摒弃了拉马克主义，因为我们都知道只有基因型中的信息可以传递。然而，从计算的角度来看，已经表明，采用拉马克模型对于某些问题可以获得良好的结果。

在拉马克模型中，局部搜索算子检查邻域（获得新特征），如果找到更好的染色体，它将成为后代。

鲍尔德温模型

鲍尔德温模型是一个中间思想，由詹姆斯·马克·鲍尔德温 (1896) 命名。在鲍尔德温模型中，染色体可以编码学习有益行为的倾向。这意味着，与拉马克模型不同，我们不会将获得的特征传递给下一代，也不会像在达尔文模型中那样完全忽略获得的特征。

鲍尔德温模型处于这两个极端之间，其中编码了个体获得某些特征的倾向，而不是特征本身。

在这个鲍尔德温模型中，局部搜索算子检查邻域（获得新特征），如果找到更好的染色体，它只会将改进的适应度分配给染色体，而不会修改染色体本身。适应度的变化表示染色体“获得特征”的能力，即使它没有直接传递给后代。

有效实施

遗传算法本质上非常通用，仅仅将其应用于任何优化问题都不会产生良好的结果。在本节中，我们将描述一些可以帮助和协助遗传算法设计者或遗传算法实施者工作的要点。

引入特定于问题的领域知识

据观察，我们向遗传算法中整合的特定于问题的领域知识越多，我们获得的目标值就越好。可以通过使用特定于问题的交叉或变异算子、自定义表示等来添加特定于问题的信息。

下图显示了 Michalewicz (1990) 对 EA 的看法：

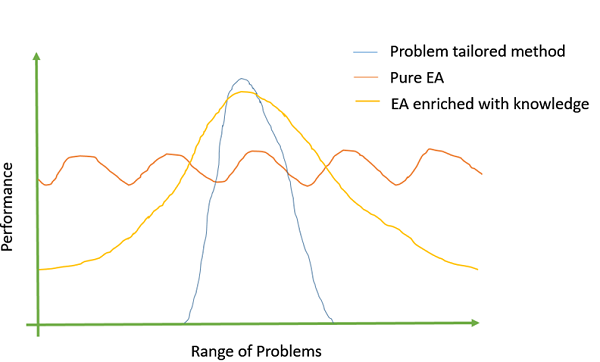
减少拥挤

拥挤发生在一个适应性很强的染色体大量繁殖时，在几代之后，整个种群都充满了具有相似适应度的相似解。这降低了多样性，而多样性是确保遗传算法成功的非常重要的因素。有很多方法可以限制拥挤。其中一些是：

变异以引入多样性。
切换到等级选择和锦标赛选择，与适应度比例选择相比，它们对适应度相似的个体施加了更大的选择压力。
适应度共享 - 在此，如果种群中已经存在类似的个体，则个体的适应度会降低。

随机化有帮助！

实验观察表明，最佳解决方案是由随机化的染色体驱动的，因为它们为种群带来了多样性。遗传算法的实现者应该注意在种群中保持足够的随机性和多样性，以获得最佳结果。

将遗传算法与局部搜索混合

局部搜索是指检查给定解邻域内的解，以寻找更好的目标值。

有时将遗传算法与局部搜索混合起来可能很有用。下图显示了在遗传算法中可以引入局部搜索的各种位置。

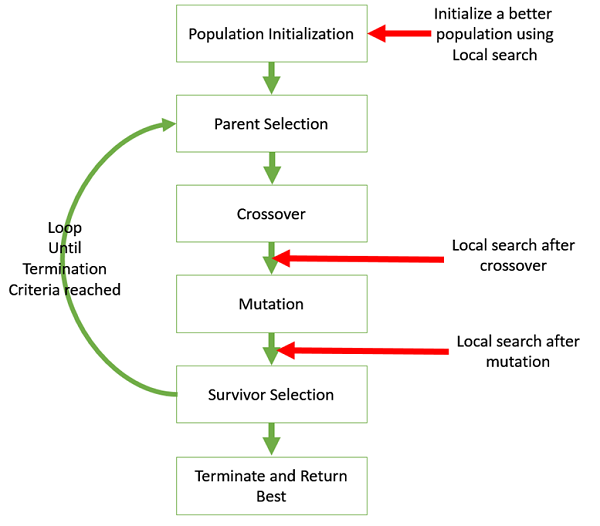
参数和技术的变异

在遗传算法中，没有“一刀切”或适用于所有问题的万能公式。即使在初始遗传算法准备就绪后，也需要花费大量时间和精力来调整参数（如种群大小、变异和交叉概率等），以找到适合特定问题的参数。

遗传算法 - 高级主题

在本节中，我们将介绍遗传算法中的一些高级主题。仅寻求遗传算法入门介绍的读者可以选择跳过本节。

约束优化问题

约束优化问题是指那些必须最大化或最小化给定目标函数值且受某些约束条件限制的优化问题。因此，并非解空间中的所有结果都是可行的，解空间包含如下所示的可行区域。

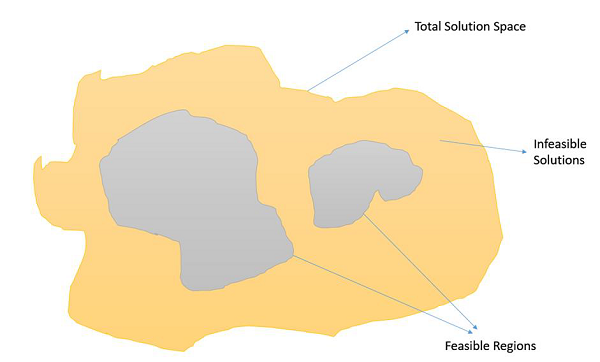
在这种情况下，交叉和变异算子可能会给我们一些不可行的解。因此，在处理约束优化问题时，必须在遗传算法中采用其他机制。

一些最常见的方法是 -

使用惩罚函数，降低不可行解的适应度，最好是使适应度与违反的约束条件数量或偏离可行区域的距离成比例地降低。
使用修复函数，接受不可行解并对其进行修改，以满足违反的约束条件。
不允许不可行解进入种群。
使用特殊的表示或解码函数，确保解的可行性。

基本理论背景

在本节中，我们将讨论模式定理和NFL定理以及构建块假设。

模式定理

研究人员一直在试图弄清楚遗传算法工作背后的数学原理，而Holland的模式定理是朝着这个方向迈出的一步。多年来，人们对模式定理进行了各种改进和建议，使其更加通用。

在本节中，我们不会深入探讨模式定理的数学原理，而是尝试对模式定理是什么有一个基本的了解。需要了解的基本术语如下 -

模式是一个“模板”。正式地，它是在字母表 = {0,1,*} 上的字符串，

其中*表示“不关心”，可以取任何值。

因此，*10*1可以表示01001、01011、11001或11011

在几何上，模式是解搜索空间中的超平面。
模式的阶是指基因中指定固定位置的数量。

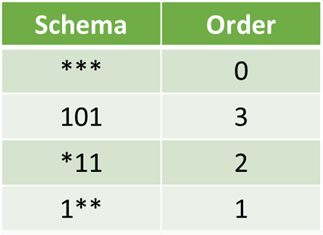
定义长度是指基因中两个最远固定符号之间的距离。

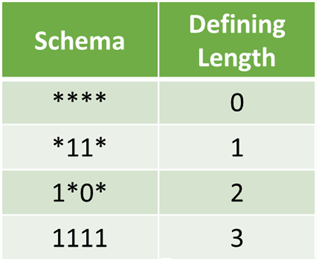
模式定理指出，具有高于平均适应度、较短定义长度和较低阶的模式更有可能在交叉和变异中存活下来。

构建块假设

构建块是具有上述给定平均适应度的低阶、低定义长度的模式。构建块假设认为，这样的构建块是遗传算法成功和适应的基础，因为它通过依次识别和重组这些“构建块”而逐步发展。

没有免费午餐（NFL）定理

Wolpert和Macready在1997年发表了一篇题为“优化问题的无免费午餐定理”的论文。它本质上指出，如果我们对所有可能问题的空间进行平均，那么所有非重复访问的黑盒算法都将表现出相同的性能。

这意味着，我们对问题的了解越多，我们的遗传算法就越针对特定问题，并且性能越好，但它会通过在其他问题上表现不佳来弥补这一点。

基于遗传算法的机器学习

遗传算法也应用于机器学习。分类器系统是一种基于遗传的机器学习（GBML）系统，在机器学习领域经常使用。GBML方法是机器学习的一种利基方法。

GBML系统有两类 -

匹兹堡方法 - 在这种方法中，一个染色体编码一个解，因此适应度分配给解。
密歇根方法 - 一个解通常由多个染色体表示，因此适应度分配给部分解。

应该记住，标准问题（如交叉、变异、拉马克式或达尔文式等）也存在于GBML系统中。

遗传算法 - 应用领域

遗传算法主要用于各种优化问题，但它们也经常用于其他应用领域。

在本节中，我们列出了遗传算法经常使用的一些领域。它们是 -

优化 - 遗传算法最常用于优化问题，在这些问题中，我们必须在给定的一组约束条件下最大化或最小化给定的目标函数值。解决优化问题的方案已在整个教程中进行了强调。
经济学 - 遗传算法还用于表征各种经济模型，如蛛网模型、博弈论均衡求解、资产定价等。
神经网络 - 遗传算法还用于训练神经网络，特别是循环神经网络。
并行化 - 遗传算法还具有非常好的并行能力，并且证明是解决某些问题的非常有效的方法，并且还为研究提供了一个很好的领域。
图像处理 - 遗传算法也用于各种数字图像处理（DIP）任务，如密集像素匹配。
车辆路径问题 - 具有多个软时间窗口、多个货运站和异构车队。
调度应用 - 遗传算法也用于解决各种调度问题，特别是时间表问题。
机器学习 - 正如已经讨论过的，基于遗传的机器学习（GBML）是机器学习中的一个利基领域。
机器人轨迹生成 - 遗传算法已被用于规划机器人手臂从一点移动到另一点所采取的路径。
飞机参数设计 - 遗传算法已被用于通过改变参数和发展更好的解决方案来设计飞机。
DNA分析 - 遗传算法已被用于使用样品的质谱数据来确定DNA的结构。
多模态优化 - 遗传算法显然是多模态优化的非常好的方法，在多模态优化中，我们必须找到多个最优解。
旅行商问题及其应用 - 遗传算法已被用于解决TSP问题，这是一个使用新颖的交叉和打包策略的著名组合问题。

遗传算法 - 进一步阅读

以下书籍可供参考，以进一步提高读者对遗传算法和进化计算的了解 -

David E. Goldberg著《搜索、优化和机器学习中的遗传算法》。
Zbigniew Michalewicz著《遗传算法 + 数据结构 = 进化程序》。
Randy L. Haupt和Sue Ellen Haupt著《实用遗传算法》。
Kalyanmoy Deb著《使用进化算法的多目标优化》。

打印页面