有效实施

遗传算法的本质非常通用，直接将其应用于任何优化问题并不能获得良好的结果。在本节中，我们将介绍一些可以帮助和指导遗传算法设计者或实施者工作的要点。

引入问题特定领域知识

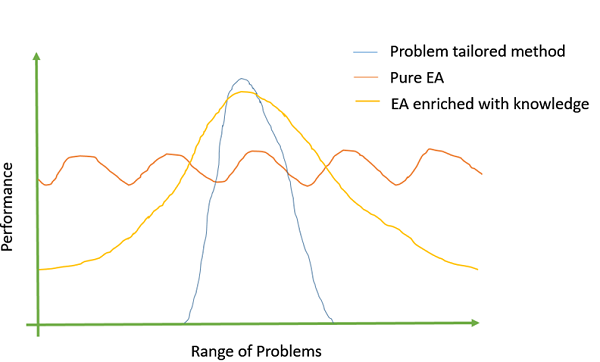
人们观察到，我们越是在遗传算法中融入问题特定的领域知识，获得的目标值就越好。可以通过使用问题特定的交叉或变异算子、自定义表示等方式添加问题特定信息。

下图显示了 Michalewicz (1990) 对进化算法的观点：

减少拥挤

当高度适应的染色体大量繁殖时，就会发生拥挤现象，并且在几代之后，整个种群就会充满具有相似适应度的相似解决方案。这减少了多样性，而多样性是确保遗传算法成功的关键因素。有很多方法可以限制拥挤。其中一些是：

• 变异以引入多样性。

• 切换到等级选择和锦标赛选择，它们比适应度比例选择对具有相似适应度的个体具有更大的选择压力。

• 适应度共享 - 在此，如果种群中已经存在相似的个体，则个体的适应度会降低。

随机化有帮助！

实验观察表明，最佳解决方案是由随机染色体驱动的，因为它们为种群带来了多样性。遗传算法实施者应注意在种群中保持足够的随机性和多样性，以获得最佳结果。

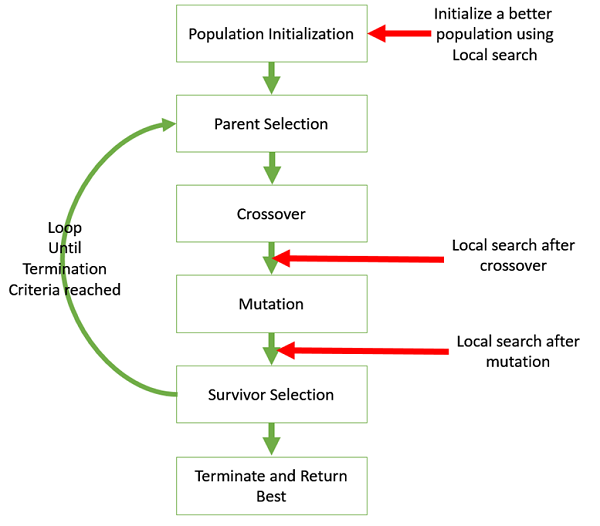
将遗传算法与局部搜索混合

局部搜索是指检查给定解决方案邻域中的解决方案以寻找更好的目标值。

有时将遗传算法与局部搜索混合起来可能很有用。下图显示了可以在遗传算法中引入局部搜索的各个位置。

参数和技术的变异

在遗传算法中，没有“一刀切”或适用于所有问题的万能公式。即使在初始遗传算法准备就绪后，也需要花费大量时间和精力来调整参数（如种群大小、变异和交叉概率等），以找到适合特定问题的参数。