
图论 - 覆盖
覆盖图是一个子图,它包含所有顶点或所有边,对应于另一个图。包含所有顶点的子图称为**线/边覆盖**。包含所有边的子图称为**顶点覆盖**。
线覆盖
令 G = (V, E) 为一个图。如果 G 的每个顶点至少与 C 中的一条边关联,则子集 C(E) 称为 G 的线覆盖,即:
deg(V) ≥ 1 ∀ V ∈ G
因为每个顶点都通过一条边与另一个顶点连接。因此,它具有至少 1 的最小度数。
示例
请查看以下图表 -
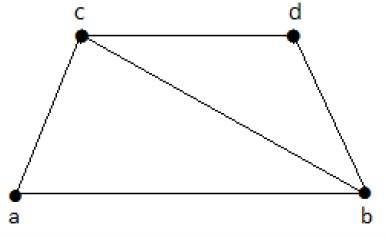
其具有线覆盖的子图如下 -
C1 = {{a, b}, {c, d}}
C2 = {{a, d}, {b, c}}
C3 = {{a, b}, {b, c}, {b, d}}
C4 = {{a, b}, {b, c}, {c, d}}
当且仅当 'G' 具有孤立顶点时,'G' 的线覆盖不存在。具有 'n' 个顶点的图的线覆盖至少具有 [n/2] 条边。
最小线覆盖
如果无法从 C 中删除任何边,则图 G 的线覆盖 C 被称为最小**线覆盖**。
示例
在上图中,具有线覆盖的子图如下 -
C1 = {{a, b}, {c, d}}
C2 = {{a, d}, {b, c}}
C3 = {{a, b}, {b, c}, {b, d}}
C4 = {{a, b}, {b, c}, {c, d}}
这里,C1、C2、C3 是最小线覆盖,而 C4 不是,因为我们可以删除 {b, c}。
最小线覆盖
它也称为**最小最小线覆盖**。具有最少边数的最小线覆盖称为 'G' 的最小线覆盖。'G' 的最小线覆盖中的边数称为 'G' 的**线覆盖数**(α1)。
示例
在上例中,C1 和 C2 是 G 的最小线覆盖,α1 = 2。
每个线覆盖都包含一个最小线覆盖。
并非每个线覆盖都包含一个最小线覆盖(C3 不包含任何最小线覆盖)。
没有最小线覆盖包含循环。
如果线覆盖 'C' 不包含长度为 3 或更长的路径,则 'C' 是一个最小线覆盖,因为 'C' 的所有分量都是星形图,并且从星形图中,无法删除任何边。
顶点覆盖
令 'G' = (V, E) 为一个图。如果 'G' 的每条边都与 'K' 中的顶点关联或被其覆盖,则 V 的子集 K 称为 'G' 的顶点覆盖。
示例
请查看以下图表 -
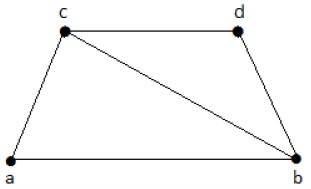
可以从上图派生的子图如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
K4 = {a, d}
这里,K1、K2 和 K3 具有顶点覆盖,而 K4 没有顶点覆盖,因为它没有覆盖边 {bc}。
最小顶点覆盖
如果无法从 'K' 中删除任何顶点,则图 'G' 的顶点 'K' 被称为最小顶点覆盖。
示例
在上图中,具有顶点覆盖的子图如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
这里,K1 和 K2 是最小顶点覆盖,而在 K3 中,可以删除顶点 'd'。
最小顶点覆盖
它也称为最小最小顶点覆盖。具有最少顶点数的图 'G' 的最小顶点覆盖称为最小顶点覆盖。
'G' 的最小顶点覆盖中的顶点数称为 G 的顶点覆盖数 (α2)。
示例
在下图中,具有顶点覆盖的子图如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
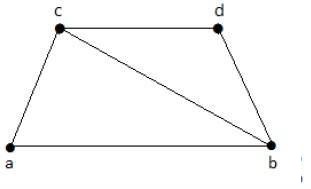
这里,K1 是 G 的最小顶点覆盖,因为它只有两个顶点。α2 = 2。