图论 - 同构

图可以以不同的形式存在，具有相同的顶点数、边数以及相同的边连通性。这样的图称为同构图。请注意，我们在本章中主要对图进行标记，以便于参考和区分它们。

同构图

如果两个图 G₁ 和 G₂ 满足以下条件，则称它们为同构：

它们的组成部分（顶点和边）数量相同。
它们的边连通性保持不变。

注意 - 简而言之，两个同构图中，一个只是另一个的修改版本。未标记的图也可以被认为是同构图。

There exists a function ‘f’ from vertices of G₁ to vertices of G₂
   [f: V(G₁) ⇒ V(G₂)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G₁, then the
edge {f(U), f(V)} ∈ G₂, then G₁ ≡ G₂.

注意

如果 G₁ ≡ G₂，则：

|V(G₁)| = |V(G₂)|

|E(G₁)| = |E(G₂)|

G₁ 和 G₂ 的度数序列相同。

如果顶点 {V₁, V₂, .. Vk} 在 G₁ 中形成长度为 K 的循环，则顶点 {f(V₁), f(V₂),… f(Vk)} 应该在 G₂ 中形成长度为 K 的循环。

以上所有条件对于图 G₁ 和 G₂ 同构都是必要的，但不足以证明这两个图是同构的。

（G₁ ≡ G₂）当且仅当（G₁− ≡ G₂−），其中 G₁ 和 G₂ 是简单图。
（G₁ ≡ G₂）如果 G₁ 和 G₂ 的邻接矩阵相同。
（G₁ ≡ G₂）当且仅当 G₁ 和 G₂ 的对应子图（通过删除 G1 中的一些顶点及其在图 G₂ 中的映像获得）是同构的。

例子

以下哪些图是同构的？

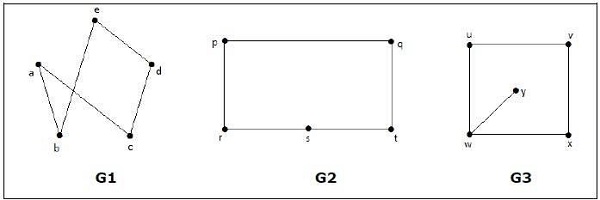
在图 G₃ 中，顶点“w”的度数仅为 3，而其他所有图顶点的度数均为 2。因此，G3 与 G₁ 或 G₂ 不同构。

取 G₁ 和 G₂ 的补图，得到：

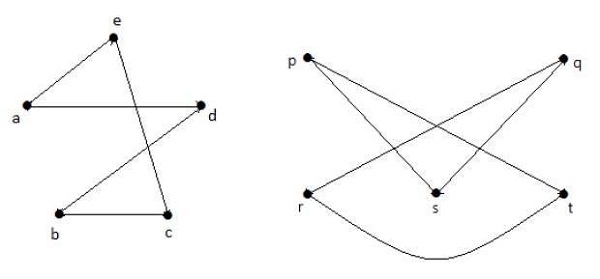
这里，（G₁− ≡ G₂−），因此（G₁ ≡ G₂）。

平面图

如果一个图“G”可以绘制在平面上或球面上，使得任意两条边在非顶点处不交叉，则称该图“G”为平面图。

例子

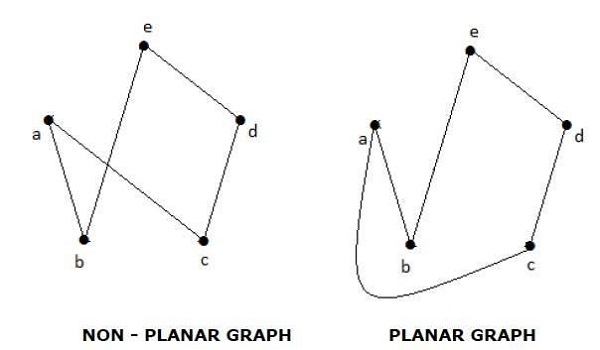
区域

每个平面图将平面划分为称为区域的连通区域。

例子

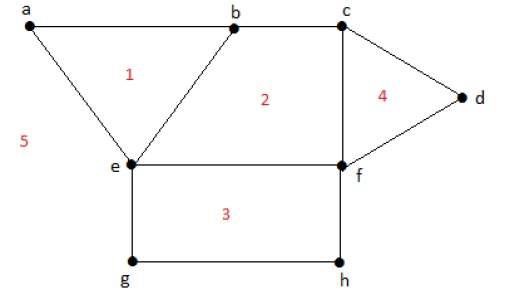
有界区域的度数r = deg(r) = 包围区域 r 的边的数量。

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8

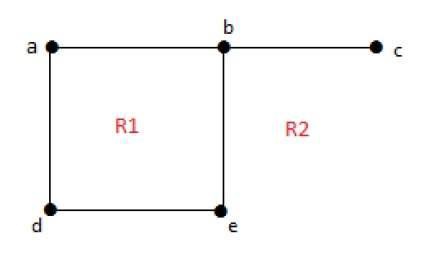
无界区域的度数r = deg(r) = 包围区域 r 的边的数量。

deg(R₁) = 4
deg(R₂) = 6

在平面图中，以下性质成立：

在一个具有“n”个顶点的平面图中，所有顶点的度数之和为：

n Σ i=1 deg(V_i) = 2|E|

根据区域度数之和/定理，在一个具有“n”个区域的平面图中，区域度数之和为：

n Σ i=1 deg(ri) = 2|E|

基于上述定理，您可以得出以下结论：

在平面图中，

如果每个区域的度数为 K，则区域度数之和为：

K|R| = 2|E|

如果每个区域的度数至少为 K（≥ K），则

K|R| ≤ 2|E|

如果每个区域的度数至多为 K（≤ K），则

K|R| ≥ 2|E|

注意 - 假设所有区域的度数相同。

根据平面图上的欧拉公式，

如果一个图“G”是连通平面图，则

|V| + |R| = |E| + 2

如果一个平面图具有“K”个连通分量，则

|V| + |R|=|E| + (K+1)

其中，|V| 是顶点数，|E| 是边数，|R| 是区域数。

边顶点不等式

如果“G”是一个连通平面图，且每个区域的度数至少为“K”，则

|E| ≤ k / (k-2) {|v| - 2}

已知，|V| + |R| = |E| + 2

K.|R| ≤ 2|E|

K(|E| - |V| + 2) ≤ 2|E|

（K - 2)|E| ≤ K(|V| - 2)

|E| ≤ k / (k-2) {|v| - 2}

如果“G”是一个简单连通平面图，则

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

存在至少一个顶点 V •∈ G，使得 deg(V) ≤ 5。

如果“G”是一个简单连通平面图（至少有 2 条边）且没有三角形，则

|E| ≤ {2|V| – 4}

库拉托夫斯基定理

一个图“G”是非平面图当且仅当“G”有一个子图与 K₅ 或 K_3,3 同胚。

同态

如果两个图 G₁ 和 G₂ 可以从同一个图“G”通过用更多顶点划分 G 的一些边得到，则称这两个图 G₁ 和 G₂ 为同态。请看下面的例子：

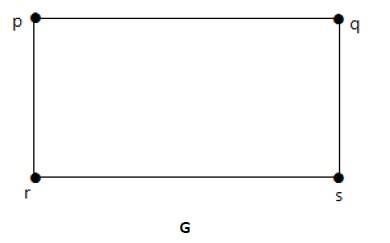
通过添加一个顶点将边“rs”分成两条边。

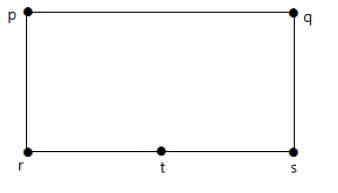
下面显示的图与第一个图同态。

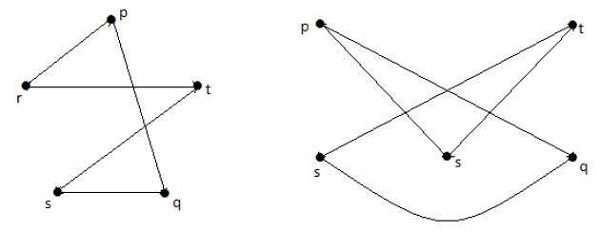
如果 G₁ 与 G₂ 同构，则 G 与 G2 同胚，但反之不一定成立。

任何具有 4 个或更少顶点的图都是平面图。
任何具有 8 个或更少边的图都是平面图。
完全图 K_n 是平面图当且仅当 n ≤ 4。
完全二部图 K_{m, n} 是平面图当且仅当 m ≤ 2 或 n ≤ 2。
具有最少顶点数的简单非平面图是完全图 K₅。
具有最少边数的简单非平面图是 K_{3, 3}。

多面体图

如果一个简单连通平面图的每个顶点的度数都≥ 3，即 deg(V) ≥ 3 ∀ V ∈ G，则称该图称为多面体图。

3|V| ≤ 2|E|
3|R| ≤ 2|E|

打印页面