图论速查指南

图论 - 绪论

在数学和计算机科学领域，图论是研究图的学科，它关注边和顶点之间的关系。它是一个热门学科，其应用遍及计算机科学、信息技术、生物科学、数学和语言学等多个领域。事不宜迟，让我们从定义图开始。

什么是图？

图是一组对象的图形表示，其中一些对象对通过链接连接。相互连接的对象由称为顶点的点表示，连接顶点的链接称为边。

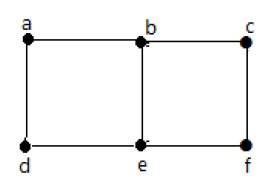
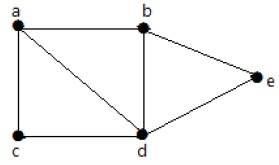
正式地说，图是一对集合(V, E)，其中V是顶点的集合，E是连接顶点对的边的集合。请看下面的图：

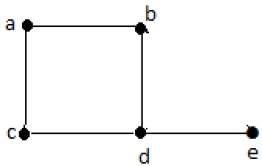
在上图中：

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

图论的应用

图论在各个工程领域都有应用：

电气工程 - 图论的概念广泛应用于电路连接的设计。连接的类型或组织称为拓扑结构。一些拓扑结构的例子包括星型、桥型、串行和并行拓扑结构。

计算机科学 - 图论用于算法的研究。例如：

克鲁斯卡尔算法
普里姆算法
迪杰斯特拉算法

计算机网络 - 网络中相互连接的计算机之间的关系遵循图论的原理。

科学 - 物质的分子结构和化学结构、生物体的DNA结构等都用图表示。

语言学 - 语言的句法树和语言的语法使用图。

一般 - 城市之间的路线可以用图表示。描绘分层有序信息（如家谱）可以用一种称为树的特殊类型的图来表示。

图论 - 基础知识

图是点和连接点的线的图表。它至少有一条线连接一组两个顶点，没有顶点连接自身。图论中的图的概念建立在一些基本术语之上，例如点、线、顶点、边、顶点的度、图的性质等。在本节中，我们将介绍这些图论的基础知识。

点

点是一维、二维或三维空间中的特定位置。为了更好地理解，可以用字母表示一个点。可以用点来表示它。

例子

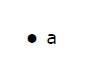
这里，点是一个名为“a”的点。

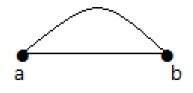
线

线是两点之间的连接。可以用实线表示。

例子

这里，“a”和“b”是点。这两点之间的连接称为线。

顶点

顶点是多条线相交的点。它也称为节点。与点类似，顶点也用字母表示。

例子

这里，顶点用字母“a”命名。

边

边是连接两个顶点的线的数学术语。许多边可以从单个顶点形成。没有顶点，就不能形成边。边必须有一个起始顶点和一个结束顶点。

例子

这里，“a”和“b”是两个顶点，它们之间的连接称为边。

图

图“G”定义为G = (V, E)，其中V是图中所有顶点的集合，E是图中所有边的集合。

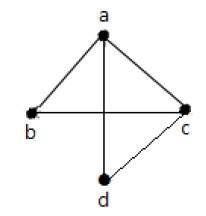
示例1

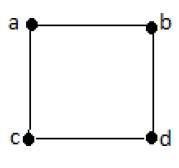
在上例中，ab、ac、cd和bd是图的边。类似地，a、b、c和d是图的顶点。

示例2

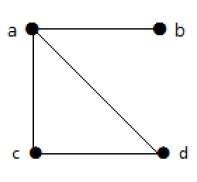
在这个图中，有四个顶点a、b、c和d，以及四条边ab、ac、ad和cd。

环

在一个图中，如果从顶点到自身画一条边，则称为环。

示例1

在上图中，V是一个顶点，它有一条边(V, V)形成一个环。

示例2

在这个图中，在顶点a和顶点b处形成了两个环。

顶点的度

它是与顶点V相邻的顶点数。

表示法 - deg(V)。

在一个具有n个顶点的简单图中，任何顶点的度为：

deg(v) ≤ n – 1 ∀ v ∈ G

一个顶点可以与除自身之外的所有其他顶点形成边。因此，顶点的度数最多为图中顶点数减1。这个1是自顶点，因为它不能自己形成环。如果任何顶点上都有环，则它不是简单图。

顶点的度数可以考虑图的两种情况：

无向图
有向图

无向图中顶点的度数

无向图没有有向边。请考虑以下示例。

示例1

请看下面的图：

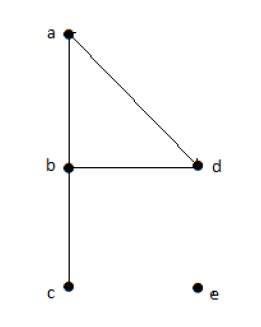
在上图中：

deg(a) = 2，因为在顶点“a”处有2条边。
deg(b) = 3，因为在顶点“b”处有3条边。
deg(c) = 1，因为在顶点“c”处形成1条边。
所以“c”是悬挂顶点。
deg(d) = 2，因为在顶点“d”处有2条边。
deg(e) = 0，因为在顶点“e”处没有形成边。
所以“e”是孤立顶点。

示例2

请看下面的图：

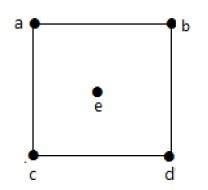
在上图中：

deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, deg(e) = 0。

顶点“e”是孤立顶点。该图没有任何悬挂顶点。

有向图中顶点的度数

在有向图中，每个顶点都有一个入度和一个出度。

图的入度

顶点V的入度是进入顶点V的边的数量。
表示法 - deg−(V)。

图的出度

顶点V的出度是从顶点V出去的边的数量。
表示法 - deg+(V)。

请考虑以下示例。

示例1

请看下面的有向图。顶点“a”有两条边，“ad”和“ab”，它们向外延伸。因此，它的出度为2。同样，有一条边“ga”指向顶点“a”。因此，“a”的入度为1。

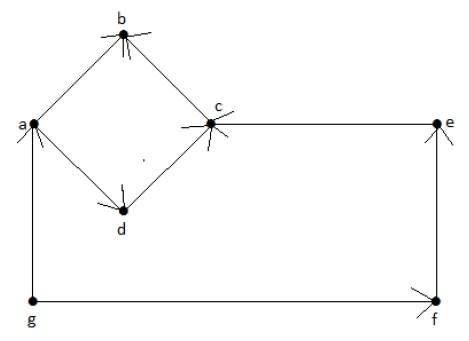
其他顶点的入度和出度如下表所示：

顶点	入度	出度
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

示例2

请看下面的有向图。顶点“a”有一条边“ae”从顶点“a”向外延伸。因此，它的出度为1。同样，该图有一条边“ba”指向顶点“a”。因此，“a”的入度为1。

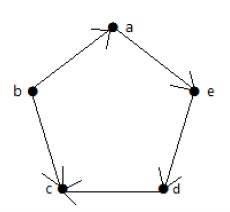
其他顶点的入度和出度如下表所示：

顶点	入度	出度
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

悬挂顶点

利用顶点的度数，我们有两种特殊的顶点类型。度数为一的顶点称为悬挂顶点。

例子

这里，在这个例子中，顶点“a”和顶点“b”有一条连接边“ab”。因此，关于顶点“a”，只有一条边指向顶点“b”，类似地，关于顶点“b”，只有一条边指向顶点“a”。最后，顶点“a”和顶点“b”的度数为一，也称为悬挂顶点。

孤立顶点

度数为零的顶点称为孤立顶点。

例子

这里，顶点“a”和顶点“b”之间没有连接，也没有与任何其他顶点连接。因此，顶点“a”和“b”的度数都为零。这些也称为孤立顶点。

邻接

以下是邻接的规范：

在一个图中，如果两个顶点之间有一条边，则称这两个顶点为邻接的。这里，顶点的邻接由连接这两个顶点的单边保持。
在一个图中，如果两条边之间有一个公共顶点，则称这两条边为邻接的。这里，边的邻接由连接两条边的单个顶点保持。

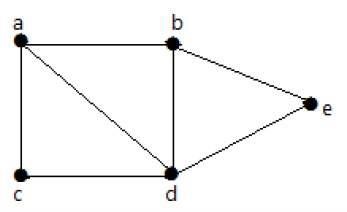
示例1

在上图中：

“a”和“b”是邻接顶点，因为它们之间有一条公共边“ab”。
“a”和“d”是邻接顶点，因为它们之间有一条公共边“ad”。
“ab”和“be”是邻接边，因为它们之间有一个公共顶点“b”。
“be”和“de”是邻接边，因为它们之间有一个公共顶点“e”。

示例2

在上图中：

“a”和“d”是邻接顶点，因为它们之间有一条公共边“ad”。
“c”和“b”是邻接顶点，因为它们之间有一条公共边“cb”。
“ad”和“cd”是邻接边，因为它们之间有一个公共顶点“d”。
“ac”和“cd”是邻接边，因为它们之间有一个公共顶点“c”。

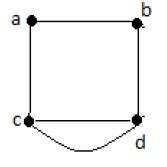
平行边

在一个图中，如果一对顶点由多于一条边连接，则这些边称为平行边。

在上图中，“a”和“b”是两个顶点，它们之间由两条边“ab”和“ab”连接。所以它被称为平行边。

多重图

具有平行边的图称为多重图。

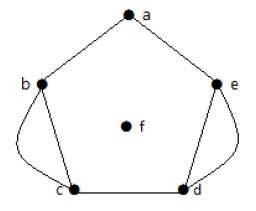
示例1

在上图中，有五条边“ab”、“ac”、“cd”、“cd”和“bd”。由于“c”和“d”之间有两条平行边，它是一个多重图。

示例2

在上图中，顶点“b”和“c”有两条边。顶点“e”和“d”之间也有两条边。因此，它是一个多重图。

图的度数序列

如果图中所有顶点的度数按降序或升序排列，则得到的序列称为该图的度数序列。

示例1

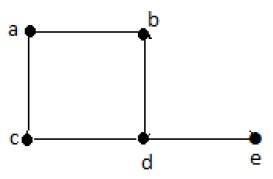
顶点	A	b	c	d	e
连接到	b,c	a,d	a,d	c,b,e	d
度数	2	2	2	3	1

在上图中，对于顶点{d, a, b, c, e}，度数序列为{3, 2, 2, 2, 1}。

示例2

顶点	A	b	c	d	e	f
连接到	b,e	a,c	b,d	c,e	a,d	-
度数	2	2	2	2	2	0

在上图中，对于顶点{a, b, c, d, e, f}，度数序列为{2, 2, 2, 2, 2, 0}。

图论 - 基本性质

图具有各种属性，这些属性用于根据图的结构对图进行表征。这些属性是用图论领域的相关术语定义的。在本节中，我们将讨论一些所有图中都常见的基本属性。

两个顶点之间的距离

这是顶点 U 和顶点 V 之间最短路径中的边数。如果有多条路径连接两个顶点，则最短路径被认为是这两个顶点之间的距离。

符号 − d(U,V)

从一个顶点到另一个顶点可能存在任意数量的路径。在这些路径中，您只需要选择最短的一条。

例子

请看下面的图：

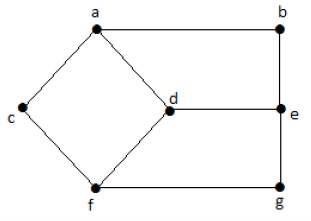
这里，从顶点“d”到顶点“e”的距离，或简称为“de”，是 1，因为它们之间只有一条边。从顶点“d”到顶点“e”有很多路径 −

da, ab, be
df, fg, ge
de（它被认为是顶点之间的距离）
df, fc, ca, ab, be
da, ac, cf, fg, ge

顶点的离心率

从一个顶点到所有其他顶点的最大距离被认为是该顶点的离心率。

符号 − e(V)

获取从特定顶点到图中所有其他顶点的距离，在这些距离中，离心率是距离中最高的。

例子

在上图中，“a”的离心率为 3。

从“a”到“b”的距离为 1（'ab'），

从“a”到“c”的距离为 1（'ac'），

从“a”到“d”的距离为 1（'ad'），

从“a”到“e”的距离为 2（'ab'-'be'）或（'ad'-'de'），

从“a”到“f”的距离为 2（'ac'-'cf'）或（'ad'-'df'），

从“a”到“g”的距离为 3（'ac'-'cf'-'fg'）或（'ad'-'df'-'fg'）。

因此，离心率为 3，这是从顶点“a”到距离最长的“ag”的最大值。

换句话说，

e(b) = 3

e(c) = 3

e(d) = 2

e(e) = 3

e(f) = 3

e(g) = 3

连通图的半径

所有顶点中的最小离心率被认为是图 G 的半径。所有顶点到所有其他顶点的最大距离中的最小值被认为是图 G 的半径。

符号 − r(G)

在图中所有顶点的离心率中，连通图的半径是所有这些离心率中的最小值。

例子

在上图中，r(G) = 2，这是“d”的最小离心率。

图的直径

所有顶点中的最大离心率被认为是图 G 的直径。所有顶点到所有其他顶点的最大距离被认为是图 G 的直径。

**符号 − d(G)** − 在图中所有顶点的离心率中，连通图的直径是所有这些离心率中的最大值。

例子

在上图中，d(G) = 3；这是最大离心率。

中心点

如果图的离心率等于其半径，则它被称为图的中心点。如果

e(V) = r(V),

则“V”是图“G”的中心点。

例子

在示例图中，“d”是图的中心点。

e(d) = r(d) = 2

中心

“G”的所有中心点的集合称为图的中心。

例子

在示例图中，{‘d’} 是图的中心。

周长

**G 的最长循环中的边数** 称为 G 的周长。

例子

在示例图中，周长为 6，我们从最长循环 a-c-f-g-e-b-a 或 a-c-f-d-e-b-a 推导出来。

围长

G 的最短循环中的边数称为其围长。

**符号：**g(G)。

**示例** − 在示例图中，图的围长为 4，我们从最短循环 a-c-f-d-a 或 d-f-g-e-d 或 a-b-e-d-a 推导出来。

顶点度数和定理

如果 G = (V, E) 是具有顶点 V = {V₁, V₂,…V_n} 的无向图，则

n Σ i=1 deg(V_i) = 2|E|

推论 1

如果 G = (V, E) 是具有顶点 V = {V₁, V₂,…V_n} 的有向图，则

n Σ i=1 deg+(V_i) = |E| = n Σ i=1 deg−(V_i)

推论 2

在任何无向图中，具有奇数度的顶点数为偶数。

推论 3

在无向图中，如果每个顶点的度数为 k，则

k|V| = 2|E|

推论 4

在无向图中，如果每个顶点的度数至少为 k，则

k|V| ≤ 2|E|

| 推论 5

在无向图中，如果每个顶点的度数最多为 k，则

k|V| ≥ 2|E|

图论 - 图的类型

根据顶点数、边数、互连性和整体结构，存在各种类型的图。本章只讨论几种重要的图类型。

空图

**没有边的图**称为空图。

例子

在上图中，有三个顶点“a”、“b”和“c”，但它们之间没有边。因此它是一个空图。

平凡图

**只有一个顶点的图**称为平凡图。

例子

在上图中，只有一个顶点“a”，没有其他边。因此它是一个平凡图。

无向图

无向图包含边，但边不是有向边。

例子

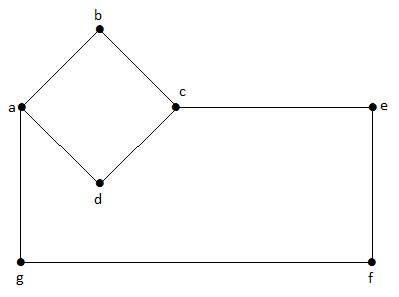
在这个图中，“a”、“b”、“c”、“d”、“e”、“f”、“g”是顶点，“ab”、“bc”、“cd”、“da”、“ag”、“gf”、“ef”是图的边。由于它是一个无向图，“ab”和“ba”是相同的。其他边也以相同的方式考虑。

有向图

在有向图中，每条边都有一个方向。

例子

在上图中，我们有七个顶点“a”、“b”、“c”、“d”、“e”、“f”和“g”，以及八条边“ab”、“cb”、“dc”、“ad”、“ec”、“fe”、“gf”和“ga”。由于它是有向图，每条边都带有箭头标记，表示其方向。请注意，在有向图中，“ab”与“ba”不同。

简单图

**没有环**且没有**平行边**的图称为简单图。

具有“n”个顶点的单个图中可能的边数最大为ⁿC₂，其中ⁿC₂ = n(n – 1)/2。
具有“n”个顶点的简单图的数量 = 2_ⁿc₂ = 2^n(n-1)/2。

例子

在下图中，有 3 个顶点和 3 条边，这是排除平行边和环的最大值。这可以使用上面的公式来证明。

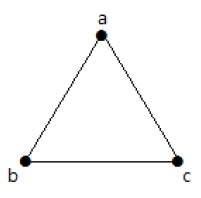
具有 n=3 个顶点的边数最大 −

ⁿC₂ = n(n–1)/2

= 3(3–1)/2

= 6/2

= 3 条边

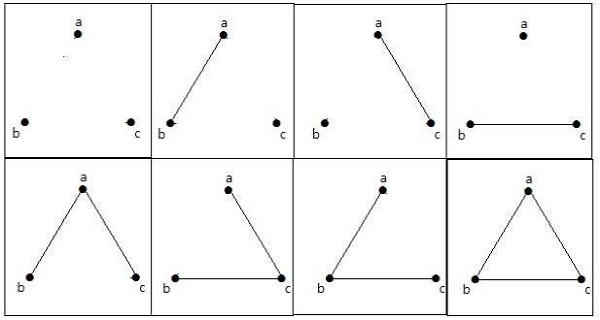
具有 n=3 个顶点的简单图的最大数量 −

2_ⁿC₂ = 2^n(n-1)/2

= 2^3(3-1)/2

= 2³

这 8 个图如下所示 −

连通图

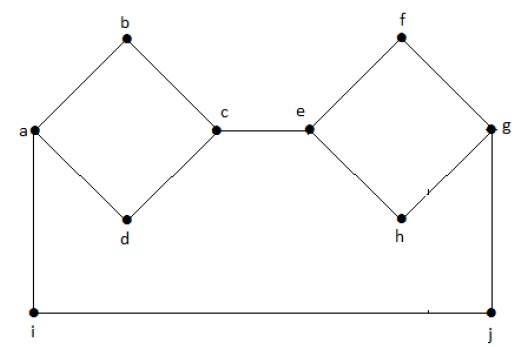
如果每对顶点之间都存在一条路径，则图 G 被称为连通图。图中每个顶点至少应该有一条边。这样我们就可以说它连接到边的另一侧的其他顶点。

例子

在下图中，每个顶点都有自己的边连接到另一条边。因此它是一个连通图。

非连通图

如果图 G 不包含至少两个连通顶点，则它是断开的。

示例1

下图是非连通图的一个例子，其中有两个分量，一个具有“a”、“b”、“c”、“d”顶点，另一个具有“e”、“f”、“g”、“h”顶点。

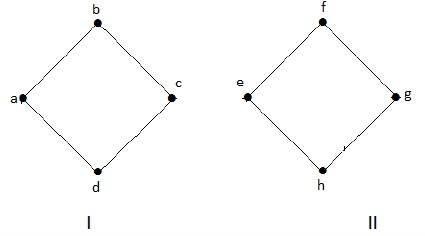
这两个分量是独立的，并且彼此不连接。因此它被称为非连通图。

示例2

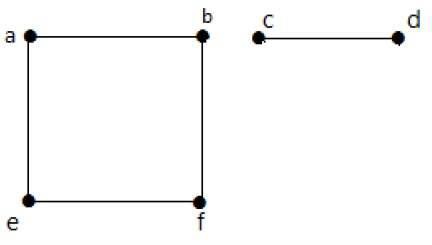
在这个例子中，有两个独立的分量，a-b-f-e 和 c-d，它们彼此不相连。因此这是一个非连通图。

正则图

如果图 G 的所有顶点具有相同的度数，则称图 G 为正则图。如果图中每个顶点的度数为“k”，则该图称为“k-正则图”。

例子

在下图中，所有顶点都具有相同的度数。因此这些图被称为正则图。

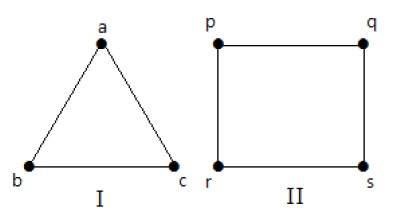
在这两个图中，所有顶点的度数都是 2。它们被称为 2-正则图。

完全图

具有“n”个互连顶点的简单图称为完全图，并用“K_n”表示。在图中，**一个顶点应该与所有其他顶点都有边连接**，则称为完全图。

换句话说，如果一个顶点连接到图中的所有其他顶点，则它被称为完全图。

例子

在下图中，图中的每个顶点都与图中的所有其他顶点连接，但自身除外。

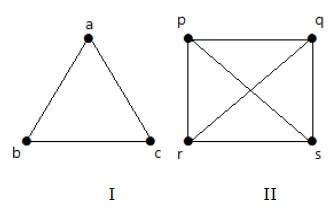
在图 I 中，

	a	b	c
a	未连接	已连接	已连接
b	已连接	未连接	已连接
c	已连接	已连接	未连接

在图 II 中，

	p	q	r	s
p	未连接	已连接	已连接	已连接
q	已连接	未连接	已连接	已连接
r	已连接	已连接	未连接	已连接
s	已连接	已连接	已连接	未连接

环图

具有“n”个顶点（n >= 3）和“n”条边的简单图，如果其所有边形成长度为“n”的环，则称为环图。

如果图中每个顶点的度数为二，则它被称为环图。

**符号** − C_n

例子

看一下下面的图 −

图 I 有 3 个顶点和 3 条边，形成环“ab-bc-ca”。
图 II 有 4 个顶点和 4 条边，形成环“pq-qs-sr-rp”。
图 III 有 5 个顶点和 5 条边，形成环“ik-km-ml-lj-ji”。

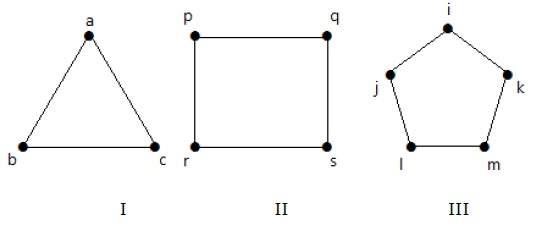
因此，所有给定的图都是环图。

轮图

通过添加一个新顶点从环图 C_n-1 获得轮图。这个新顶点称为**中心**，它与 C_n 的所有顶点相连。

符号 − W_n

W_n 中的边数 = 中心到所有其他顶点的边数 +

环图中所有其他节点（无中心）的边数。

= (n–1) + (n–1)

= 2(n–1)

例子

看一下下面的图。它们都是轮图。

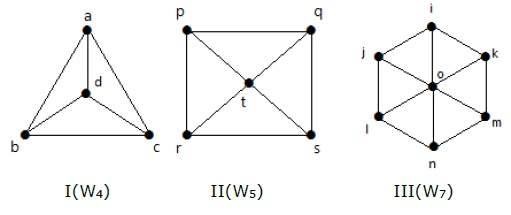
在图 I 中，它是通过在中间添加一个名为“d”的顶点从 C₃ 获得的。它表示为 W₄。

W4 中的边数 = 2(n-1) = 2(3) = 6

在图 II 中，它是通过在中间添加一个名为“t”的顶点从 C4 获得的。它表示为 W₅。

W5 中的边数 = 2(n-1) = 2(4) = 8

图 III 是由 C₆ 添加一个名为“o”的中间顶点得到的。它表示为 W₇。

W₄ 中边的数量 = 2(n-1) = 2(6) = 12

循环图

至少包含一个环的图称为循环图。

例子

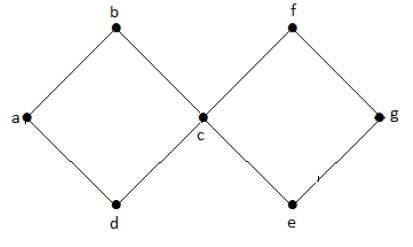
在上例图中，我们有两个环 a-b-c-d-a 和 c-f-g-e-c。因此它被称为循环图。

无环图

没有环的图称为无环图。

例子

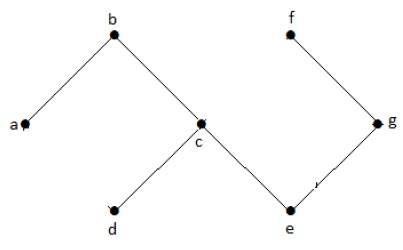
在上例图中，我们没有任何环。因此它是一个无环图。

二分图

顶点划分 V = {V₁, V₂} 的简单图 G = (V, E) 如果**E 的每条边都连接 V₁ 中的一个顶点和 V₂ 中的一个顶点**，则称为二分图。

一般来说，二分图有两个顶点集，例如 V₁ 和 V₂，如果画一条边，它应该连接 V₁ 集中的任何顶点到 V₂ 集中的任何顶点。

例子

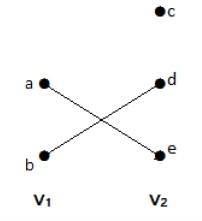
在这个图中，您可以观察到两组顶点——V₁ 和 V₂。这里，名为“ae”和“bd”的两条边连接着 V₁ 和 V₂ 两组的顶点。

完全二分图

如果划分 V = {V₁, V₂} 的二分图“G”，G = (V, E) 中 V₁ 的每个顶点都连接到 V₂ 的每个顶点，则称其为完全二分图。

一般来说，完全二分图连接 V₁ 集中的每个顶点到 V₂ 集中的每个顶点。

例子

下图是一个完全二分图，因为它有连接 V₁ 集中每个顶点到 V₂ 集中每个顶点的边。

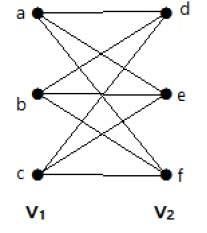
如果 |V₁| = m 且 |V₂| = n，则完全二分图表示为 K_{m, n}。

K_m,n 有 (m+n) 个顶点和 (mn) 条边。
如果 m=n，则 K_m,n 是一个正则图。

一般来说，**完全二分图不是完全图**。

如果 m=n=1，则 K_m,n 是一个完全图。

具有 n 个顶点的二分图中边的最大数量为：

[n²/4]

如果 n=10，k_{5, 5} = [n²/4] = [10²/4] = 25。

同样，K_{6, 4}=24

K_{7, 3}=21

K_{8, 2}=16

K_{9, 1}=9

如果 n=9，k_{5, 4} = [n²/4] = [9²/4] = 20

同样，K_{6, 3}=18

K_{7, 2}=14

K_{8, 1}=8

如果“G”没有奇数长度的环，“G”就是一个二分图。二分图的一个特例是星形图。

星形图

形式为 K_{1, n-1} 的完全二分图是一个具有 n 个顶点的星形图。如果单个顶点属于一个集合，而所有剩余顶点属于另一个集合，则星形图是完全二分图。

例子

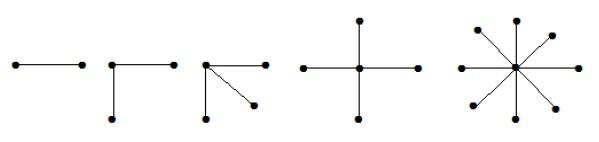
在上图中，“n”个顶点中，所有“n-1”个顶点都连接到单个顶点。因此，它具有 K¹, ^n-1 的形式，它们是星形图。

图的补图

设“G−”是一个简单图，其顶点与“G”相同，如果边{U, V}不存在于 G 中，则边{U, V}存在于“G−”中。这意味着，如果两个顶点在 G 中不相邻，则它们在“G−”中相邻。

如果图 I 中存在的边在另一个图 II 中不存在，并且如果图 I 和图 II 组合在一起形成一个完全图，则图 I 和图 II 互称为补图。

例子

在下面的例子中，图 I 有两条边“cd”和“bd”。其补图 II 有四条边。

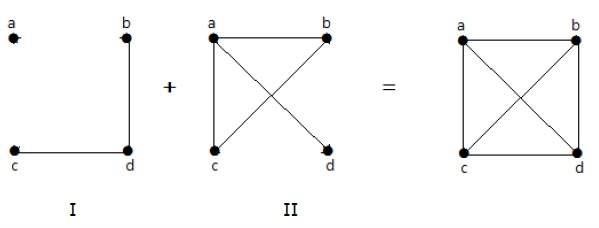
请注意，图 I 中的边不存在于图 II 中，反之亦然。因此，两图的组合给出了“n”个顶点的完全图。

**注意**——两个补图的组合构成一个完全图。

如果“G”是任何简单图，则

|E(G)| + |E('G-')| = |E(K_n)|，其中 n = 图中顶点的数量。

例子

设“G”是一个具有九个顶点和十二条边的简单图，求“G−”中的边数。

你有，|E(G)| + |E('G-')| = |E(K_n)|

12 + |E('G-')| =

9(9-1) / 2 = ⁹C₂

12 + |E('G-')| = 36

|E('G-')| = 24

“G”是一个具有 40 条边和其补图“G−”具有 38 条边的简单图。求图 G 或“G−”中的顶点数。

设图中顶点的数量为“n”。

我们有，|E(G)| + |E('G-')| = |E(K_n)|

40 + 38 = n(n-1)/2

78 = n(n-1)/2

156 = n(n-1)

13 × 12 = n(n-1)

图论 - 树

树是即使不包含单个环的图。它们以图形形式表示分层结构。树属于最简单的图类。尽管它们很简单，但它们具有丰富的结构。

树提供了一系列有用的应用程序，从简单的家谱到计算机科学数据结构中的树。

树

**连通的无环图**称为树。换句话说，没有环的连通图称为树。

树的边称为**分支**。树的元素称为其节点。没有子节点的节点称为**叶节点**。

具有“n”个顶点的树具有“n-1”条边。如果它比“n-1”多一条边，则额外的边显然必须与两个顶点配对，从而形成一个环。然后，它变成一个循环图，这违反了树图的规定。

示例1

此处显示的图是一棵树，因为它没有环并且是连通的。它有四个顶点和三条边，即对于“n”个顶点“n-1”条边，如定义中所述。

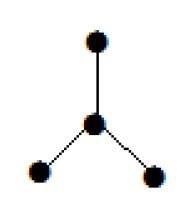
**注意**——每棵树至少有两个度数为一的顶点。

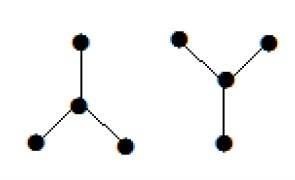
示例2

在上例中，顶点“a”和“d”的度数为一。其他两个顶点“b”和“c”的度数为二。这是可能的，因为为了不形成环，图中至少应该有两个单边。它只不过是两个度数为一的边。

森林

**不连通的无环图**称为森林。换句话说，树的不相交集合称为森林。

例子

下图看起来像两个子图；但它是一个单一的不连通图。此图中没有环。因此，它显然是一个森林。

生成树

设 G 为连通图，则 G 的子图 H 称为 G 的生成树，如果：

H 是一棵树
H 包含 G 的所有顶点。

无向图 G 的生成树 T 是包含 G 所有顶点的子图。

例子

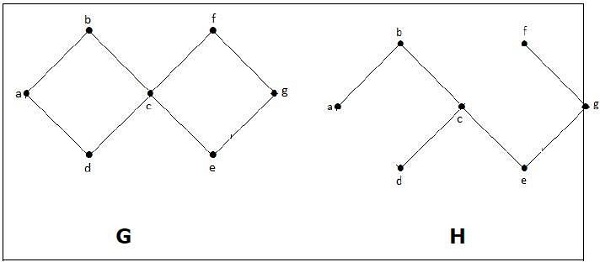
在上例中，G 是连通图，H 是 G 的子图。

显然，图 H 没有环，它是一棵具有六条边的树，比顶点总数少一条。因此，H 是 G 的生成树。

回路秩

设“G”是具有“n”个顶点和“m”条边的连通图。“G”的生成树“T”包含 (n-1) 条边。

因此，为了得到生成树，你需要从“G”中删除的边数 = m-(n-1)，这称为 G 的回路秩。

这个公式是正确的，因为在生成树中，你需要有“n-1”条边。在“m”条边中，你需要在图中保留“n-1”条边。

因此，从“m”中删除“n-1”条边得到为了获得不应形成环的生成树而需要从图中删除的边。

例子

请看下面的图：

对于上例中给出的图，你有 m=7 条边和 n=5 个顶点。

则回路秩为：

G = m – (n – 1)

= 7 – (5 – 1) = 3

= 3

例子

设“G”是一个具有六个顶点且每个顶点的度数为三的连通图。求“G”的回路秩。

根据顶点度数之和定理：

**n Σ i=1** deg(V_i) = 2|E|

6 × 3 = 2|E|

|E| = 9

回路秩 = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

基尔霍夫定理

基尔霍夫定理可用于查找可以从连通图中形成的生成树的数量。

例子

矩阵“A”填充如下：如果两个顶点之间存在边，则应将其指定为“1”，否则为“0”。

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

使用基尔霍夫定理，应将其更改为将主对角线值替换为顶点的度数，并将所有其他元素替换为 -1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$M_{11}的余子式= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

因此，生成树的数量 = 8。

图论 - 连通性

是否可以从一个顶点遍历到另一个顶点取决于图的连接方式。连通性是图论中的一个基本概念。连通性定义了图是连通的还是不连通的。它根据边和顶点有子主题，称为边连通性和顶点连通性。让我们详细讨论它们。

连通性

如果每对顶点之间都存在一条路径，则称图是**连通的**。从每个顶点到任何其他顶点，都应该有一些路径可供遍历。这称为图的连通性。具有多个不连通顶点和边的图称为不连通图。

示例1

在下图中，可以从一个顶点遍历到任何其他顶点。例如，可以使用路径“a-b-e”从顶点“a”遍历到顶点“e”。

示例2

在下面的例子中，无法从顶点“a”遍历到顶点“f”，因为它们之间没有直接或间接的路径。因此它是一个不连通图。

割顶

设“G”是一个连通图。如果“G-V”（从“G”中删除“V”）导致不连通图，则顶点 V ∈ G 称为“G”的割顶。从图中移除割顶会将其分成两个或多个图。

**注意**——移除割顶可能会使图不连通。

连通图“G”最多可能有 (n-2) 个割顶。

例子

在下图中，顶点“e”和“c”是割顶。

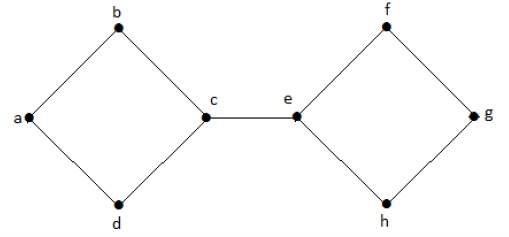
通过移除“e”或“c”，图将变成不连通图。

没有“g”，顶点“c”和顶点“h”以及许多其他顶点之间没有路径。因此它是一个不连通图，其割顶为“e”。同样，“c”也是上图的割顶。

割边（桥）

设“G”是一个连通图。如果“G-e”导致不连通图，则边“e”∈ G 称为割边。

如果移除图中的一条边会导致两个或多个图，则该边称为割边。

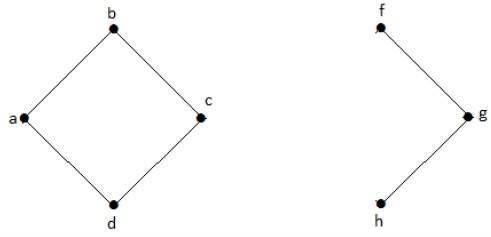
例子

在下图中，割边是 [(c, e)]。

通过从图中移除边 (c, e)，它变成了不连通图。

在上图中，移除边 (c, e) 将图分成两个，这实际上是一个不连通图。因此，边 (c, e) 是该图的割边。

**注意**——设“G”是一个具有“n”个顶点的连通图，则

边“e”∈ G 是割边当且仅当边“e”不是 G 中任何环的一部分。
可能的割边最大数量为“n-1”。
只要存在割边，就一定存在割顶，因为至少割边的一个顶点是割顶。
如果存在割顶，则割边可能存在也可能不存在。

图的割集

设‘G’=(V, E)是一个连通图。E 的子集 E’ 称为 G 的割集，如果从 G 中删除 E’ 中的所有边会使 G 不连通。

如果从图中删除一定数量的边使其不连通，则这些被删除的边称为该图的割集。

例子

看下面的图。它的割集是 E1 = {e1, e3, e5, e8}。

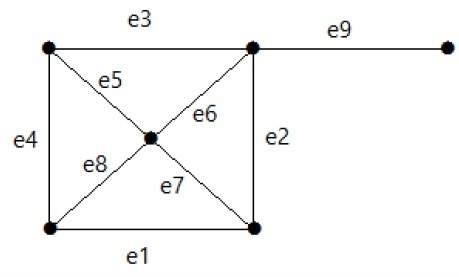
从图中移除割集 E1 后，图将如下所示：

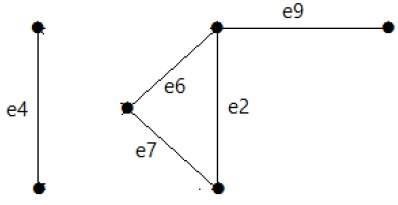
同样，还有其他可以使图不连通的割集：

E3 = {e9} – 图中最小的割集。
E4 = {e3, e4, e5}

边连通度

设‘G’是一个连通图。删除最少数量的边使得‘G’不连通的边的数量称为 G 的边连通度。

符号 − λ(G)

换句话说，G 的最小割集中边的数量称为 G 的边连通度。

如果‘G’有一条割边，则 λ(G) 为 1。（G 的边连通度。）

例子

看下面的图。通过移除两条最小边，连通图变得不连通。因此，它的边连通度 (λ(G)) 为 2。

以下是通过移除两条边使图不连通的四种方法：

点连通度

设‘G’是一个连通图。删除最少数量的顶点使得‘G’不连通或将‘G’简化为平凡图的顶点数称为它的点连通度。

符号 − K(G)

例子

在上图中，移除顶点‘e’和‘i’使图不连通。

如果 G 有一个割顶，则 K(G) = 1。

符号 − 对于任何连通图 G，

K(G) ≤ λ(G) ≤ δ(G)

点连通度 (K(G))，边连通度 (λ(G))，G 的最小度数 (δ(G))。

例子

计算下列图的 λ(G) 和 K(G)：

解答

从图中，

δ(G) = 3

K(G) ≤ λ(G) ≤ δ(G) = 3 (1)

K(G) ≥ 2 (2)

删除边 {d, e} 和 {b, h}，我们可以使 G 不连通。

因此，

λ(G) = 2

2 ≤ λ(G) ≤ δ(G) = 2 (3)

从 (2) 和 (3)，点连通度 K(G) = 2

图论 - 覆盖

覆盖图是一个子图，它包含所有顶点或与某个其他图对应的所有边。包含所有顶点的子图称为线/边覆盖。包含所有边的子图称为点覆盖。

线覆盖

设 G = (V, E) 为一个图。C(E) 的一个子集称为 G 的线覆盖，如果 G 的每个顶点都至少与 C 中的一条边关联，即

deg(V) ≥ 1 ∀ V ∈ G

因为每个顶点都通过一条边与另一个顶点相连。因此它至少有 1 度。

例子

请看下面的图：

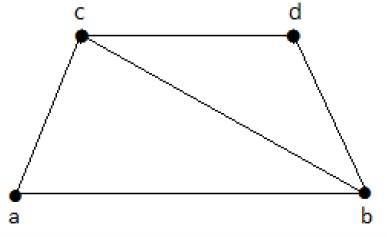
其具有线覆盖的子图如下：

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

当且仅当‘G’有一个孤立顶点时，‘G’不存在线覆盖。具有‘n’个顶点的图的线覆盖至少有 [n/2] 条边。

最小线覆盖

如果不能从 C 中删除任何边，则图 G 的线覆盖 C 称为最小线覆盖。

例子

在上图中，具有线覆盖的子图如下：

C₁ = {{a, b}, {c, d}}

C₂ = {{a, d}, {b, c}}

C₃ = {{a, b}, {b, c}, {b, d}}

C₄ = {{a, b}, {b, c}, {c, d}}

这里，C₁、C₂、C₃是最小线覆盖，而 C₄ 不是，因为我们可以删除 {b, c}。

最小线覆盖

也称为最小最小线覆盖。具有最少边数的最小线覆盖称为‘G’的最小线覆盖。‘G’的最小线覆盖中的边数称为‘G’的线覆盖数 (α₁)。

例子

在上面的例子中，C₁和 C₂是 G 的最小线覆盖，并且 α₁ = 2。

每个线覆盖都包含一个最小线覆盖。
并非每个线覆盖都包含一个最小线覆盖（C₃不包含任何最小线覆盖）。
任何最小线覆盖都不包含环。
如果线覆盖‘C’不包含长度为 3 或更长的路径，则‘C’是最小线覆盖，因为‘C’的所有分量都是星图，并且从星图中不能删除任何边。

点覆盖

设‘G’ = (V, E) 为一个图。V 的子集 K 称为‘G’的点覆盖，如果‘G’的每条边都与 K 中的一个顶点关联或被 K 中的一个顶点覆盖。

例子

请看下面的图：

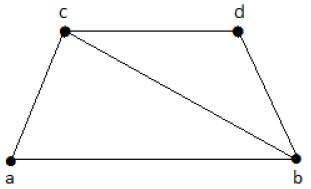
可以从上图导出的子图如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

K₄ = {a, d}

这里，K₁、K₂和 K₃具有点覆盖，而 K₄没有任何点覆盖，因为它没有覆盖边 {bc}。

最小点覆盖

如果不能从‘K’中删除任何顶点，则图‘G’的顶点‘K’称为最小点覆盖。

例子

在上图中，具有点覆盖的子图如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

这里，K₁和 K₂是最小点覆盖，而在 K₃中，可以删除顶点‘d’。

最小点覆盖

也称为最小最小点覆盖。具有最少顶点数的图‘G’的最小点覆盖称为最小点覆盖。

‘G’的最小点覆盖中的顶点数称为 G 的点覆盖数 (α₂)。

例子

在下图中，具有点覆盖的子图如下：

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

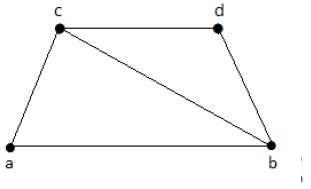
这里，K₁是 G 的最小点覆盖，因为它只有两个顶点。α₂ = 2。

图论 - 匹配

匹配图是一个图的子图，其中没有边彼此相邻。简单地说，任何两条边之间都不应有任何公共顶点。

匹配

设‘G’ = (V, E) 为一个图。如果G 的每个顶点最多与 M 中的一条边关联，则子图称为匹配 M(G)，即

deg(V) ≤ 1 ∀ V ∈ G

这意味着在匹配图 M(G) 中，顶点的度数应为 1 或 0，其中边应来自图 G。

符号 − M(G)

例子

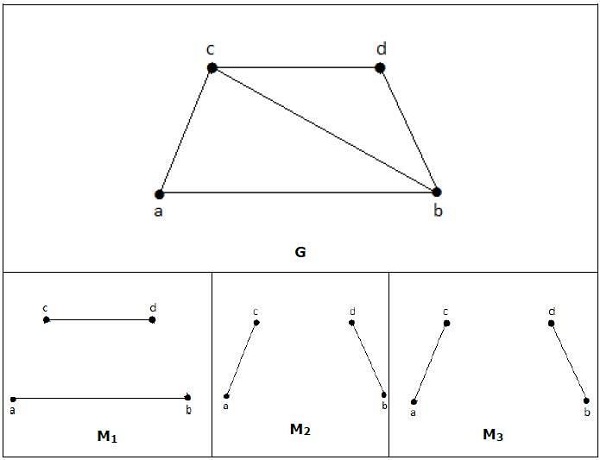
在匹配中，

如果 deg(V) = 1，则 (V) 被称为匹配的

如果 deg(V) = 0，则 (V) 没有匹配。

在匹配中，没有两条边是相邻的。这是因为如果任何两条边相邻，则连接这两条边的顶点的度数将为 2，这违反了匹配规则。

极大匹配

如果不能将‘G’的其他边添加到 M，则图‘G’的匹配 M 称为极大匹配。

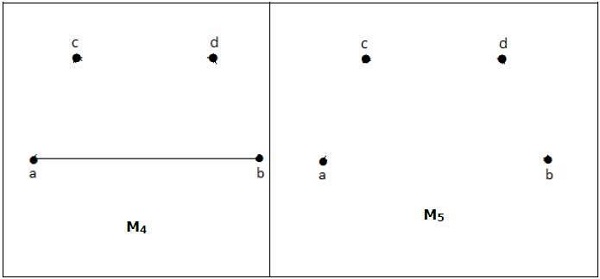
例子

上图中的 M1、M2、M3 是 G 的极大匹配。

最大匹配

也称为最大极大匹配。最大匹配定义为具有最大边数的极大匹配。

‘G’的最大匹配中的边数称为其匹配数。

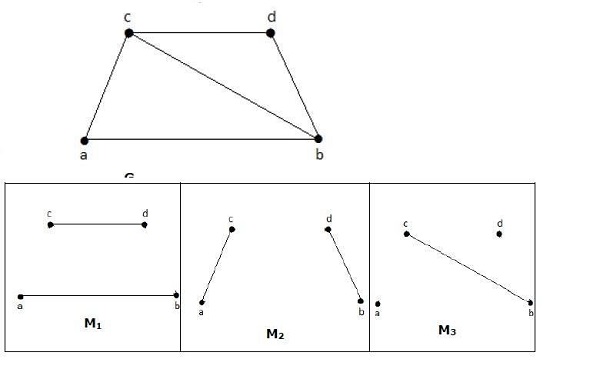
例子

对于上面例子中给出的图，M1 和 M2 是‘G’的最大匹配，其匹配数为 2。因此，使用图 G，我们最多只能形成只有 2 条边的子图。因此，匹配数为 2。

完美匹配

如果图 g (G) 的每个顶点都恰好与匹配 (M) 的一条边关联，则图 (G) 的匹配 (M) 称为完美匹配，即

deg(V) = 1 ∀ V

子图中每个顶点的度数都应为 1。

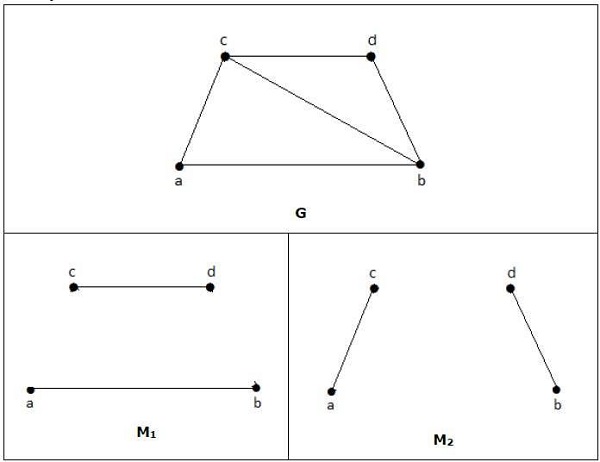
例子

在下图中，M1 和 M2 是 G 的完美匹配的例子。

注意 − 图的每个完美匹配也是图的最大匹配，因为在完美匹配图中不可能再添加一条边。

图的最大匹配不必是完美的。如果图‘G’有一个完美匹配，则顶点数 |V(G)| 为偶数。如果它是奇数，则最后一个顶点与另一个顶点配对，最终剩下一个单个顶点，它不能与任何其他顶点配对，其度数为零。这显然违反了完美匹配原则。

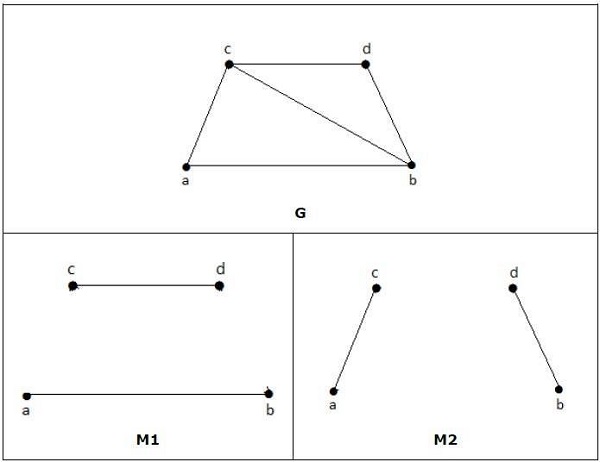
例子

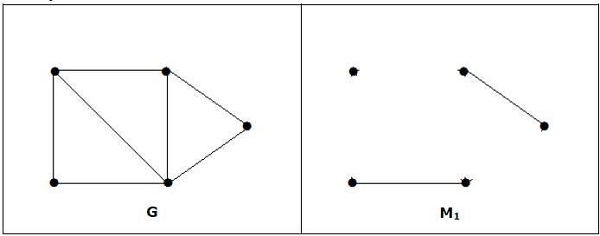
注意 − 上述语句的反面不一定为真。如果 G 具有偶数个顶点，则 M1 不必是完美的。

例子

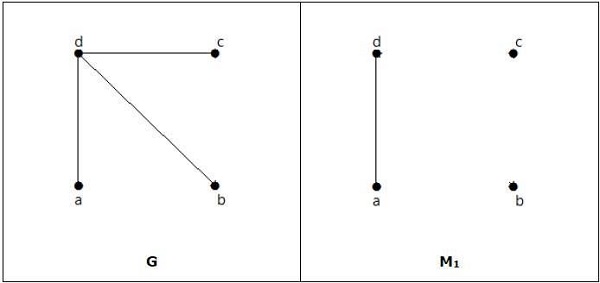
它是匹配，但它不是完美匹配，即使它有偶数个顶点。

图论 - 独立集

独立集用集合表示，其中

不应有任何彼此相邻的边。任何两条边之间都不应有任何公共顶点。
不应有任何彼此相邻的顶点。任何两个顶点之间都不应有任何公共边。

独立线集

设‘G’ = (V, E) 为一个图。E 的子集 L 称为‘G’的独立线集，如果 L 中的任何两条边都不相邻。这样的集合称为独立线集。

例子

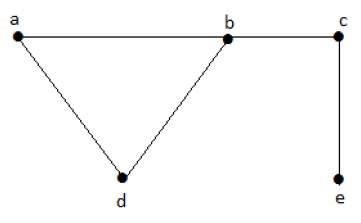
让我们考虑以下子集：

L₁ = {a,b}
L₂ = {a,b} {c,e}
L₃ = {a,d} {b,c}

在这个例子中，子集 L2 和 L3 明显不是给定图中的相邻边。它们是独立线集。但是 L1 不是独立线集，因为要构成独立线集，至少应该有两条边。

极大独立线集

如果不能将‘G’的其他边添加到‘L’，则独立线集称为图‘G’的极大独立线集。

例子

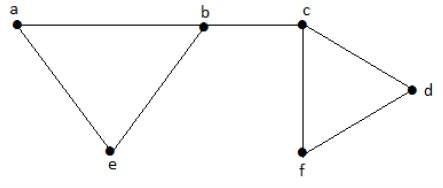
让我们考虑以下子集：

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L₂和 L₃是极大独立线集/极大匹配。因为只有对于这两个子集，没有机会添加任何非相邻的边。因此，这两个子集被认为是极大独立线集。

最大独立线集

具有最大边数的‘G’的最大独立线集称为‘G’的最大独立线集。

Number of edges in a maximum independent line set of G (β₁)
   = Line independent number of G
   = Matching number of G

例子

让我们考虑以下子集：

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L₃是 G 的最大独立线集，具有图中不相邻的最大边数，记作 β1 = 3。

注意 − 对于任何没有孤立顶点的图 G，

α1 + β1 = 图中的顶点数 = |V|

例子

K_n/C_n/w_n 的线覆盖数，

$$α 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:如果\:n\:是偶数 \\\frac{n+1}{2}\:如果\:n\:是奇数\end{cases}$$

独立线数（匹配数）= β₁ = [n/2] α₁ + β₁ = n。

独立顶点集

设‘G’ = (V, E) 为一个图。如果‘S’中没有两个顶点相邻，则‘V’的一个子集称为‘G’的独立集。

例子

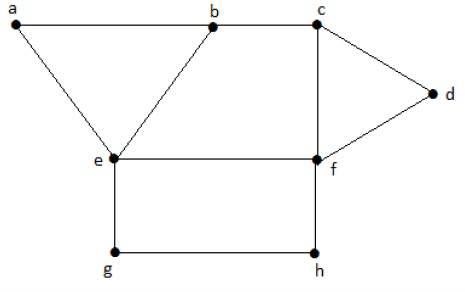
考虑上图中的以下子集：

S₁ = {e}

S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

显然，S₁不是一个独立顶点集，因为要得到一个独立顶点集，图中至少应该有两个顶点。但这里并非如此。子集S₂、S₃和S₄是独立顶点集，因为没有一个顶点与子集中的任何一个顶点相邻。

最大独立顶点集

设“G”是一个图，则当“G”的任何其他顶点都不能添加到“S”中时，“G”的独立顶点集被称为最大独立顶点集。

例子

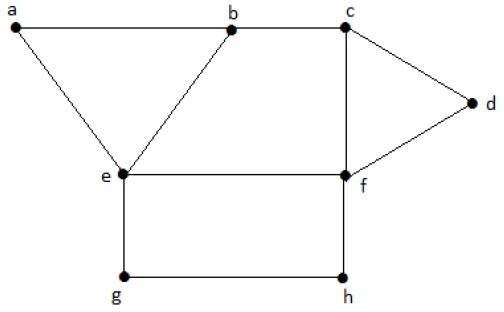
考虑上述图中的以下子集。

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

S₂和S₃是“G”的最大独立顶点集。在S₁和S₄中，我们可以添加其他顶点；但在S₂和S₃中，我们不能添加任何其他顶点。

最大独立顶点集

具有最大顶点数的“G”的最大独立顶点集称为最大独立顶点集。

例子

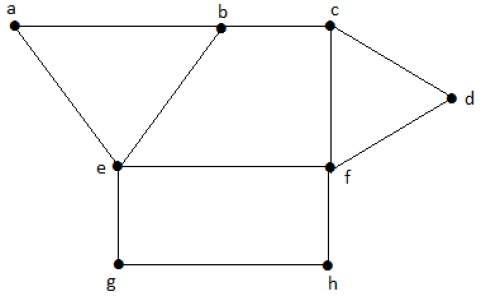
考虑上述图中的以下子集：

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

只有S₃是最大独立顶点集，因为它包含最多的顶点。 “G”的最大独立顶点集中的顶点数称为G的独立顶点数 (β₂)。

例子

对于完全图K_n，

顶点覆盖数 = α₂ = n−1

顶点独立数 = β₂ = 1

α₂ + β₂ = n

在一个完全图中，每个顶点与其剩余的 (n − 1) 个顶点相邻。因此，K_n的最大独立集只包含一个顶点。

因此，β₂=1

且α₂=|v| − β₂ = n-1

注意 − 对于任何图“G” = (V, E)

α₂ + β₂ = |v|
如果“S”是“G”的独立顶点集，则 (V – S) 是G的顶点覆盖。

图论 - 着色

图着色只不过是在某些约束下对图组件（例如顶点、边和区域）进行标记的一种简单方法。在一个图中，没有两个相邻的顶点、相邻的边或相邻的区域用最少的颜色着色。这个数字称为色数，该图称为正确着色的图。

在图着色中，对图设置的约束包括颜色、着色顺序、颜色分配方式等。颜色赋予顶点或特定区域。因此，具有相同颜色的顶点或区域形成独立集。

顶点着色

顶点着色是将颜色分配给图“G”的顶点，以使任何两个相邻顶点都不具有相同的颜色。简而言之，边的两个顶点不应具有相同的颜色。

色数

图“G”顶点着色所需的最小颜色数称为G的色数，记为X(G)。

当且仅当'G'是空图时，χ(G) = 1。如果'G'不是空图，则χ(G) ≥ 2。

例子

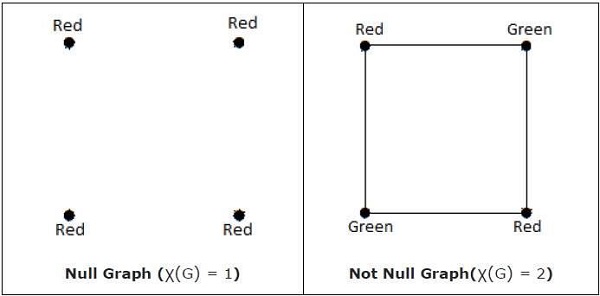
注意 − 如果存在一个最多使用n种颜色的顶点着色，则称图“G”是n可着色的，即X(G) ≤ n。

区域着色

区域着色是将颜色分配给平面图的区域，以使任何两个相邻区域都不具有相同的颜色。如果两个区域具有公共边，则称它们为相邻区域。

例子

看一下下面的图。区域“aeb”和“befc”是相邻的，因为这两个区域之间有公共边“be”。

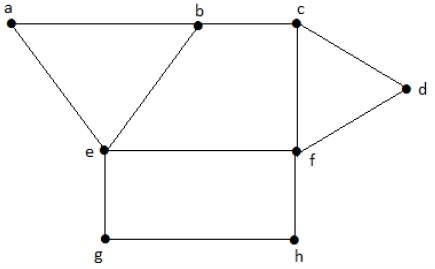
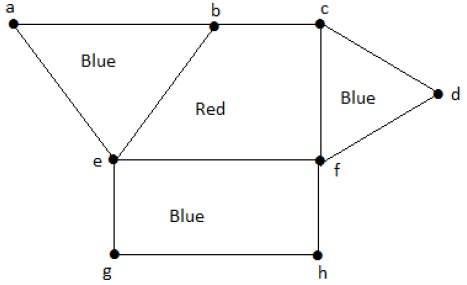
类似地，其他区域也根据邻接关系着色。此图着色如下：

例子

Kn的色数是

n
n–1
[n/2]
[n/2]

考虑K₄的这个例子。

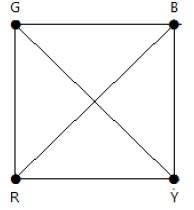
在完全图中，每个顶点与其剩余的 (n – 1) 个顶点相邻。因此，每个顶点都需要一种新颜色。因此，K_n的色数 = n。

图着色的应用

图着色是图论中最重要的概念之一。它用于计算机科学的许多实时应用中，例如：

聚类
数据挖掘
图像采集
图像分割
网络
资源分配
进程调度

图论 - 同构

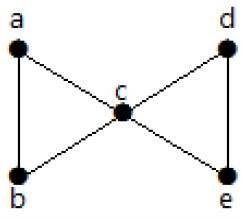
图可以以不同的形式存在，具有相同的顶点数、边数以及相同的边连通性。这样的图称为同构图。请注意，本章中我们主要为了参考和区分这些图而对它们进行标记。

同构图

如果满足以下条件，则两个图G₁和G₂被称为同构：

它们的组件数（顶点和边）相同。
它们的边连通性保持不变。

注意 − 简而言之，在两个同构图中，一个图是另一个图的修改版本。未标记的图也可以被认为是同构图。

There exists a function ‘f’ from vertices of G₁ to vertices of G₂
   [f: V(G₁) ⇒ V(G₂)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G₁, then the
edge {f(U), f(V)} ∈ G₂, then G₁ ≡ G₂.

注意

如果G₁ ≡ G₂，则：

|V(G₁)| = |V(G₂)|

|E(G₁)| = |E(G₂)|

G₁和G₂的度数序列相同。

如果顶点 {V₁, V₂, .. Vk} 在G₁中形成长度为K的环，则顶点 {f(V₁), f(V₂),… f(Vk)} 应在G₂中形成长度为K的环。

所有上述条件对于图G₁和G₂是同构的都是必要的，但不足以证明这些图是同构的。

(G₁ ≡ G₂) 当且仅当 (G₁− ≡ G₂−)，其中G₁和G₂是简单图。
(G₁ ≡ G₂) 如果G₁和G₂的邻接矩阵相同。
(G₁ ≡ G₂) 当且仅当G₁和G₂的对应子图（通过删除G1中的一些顶点及其在图G₂中的镜像获得）是同构的。

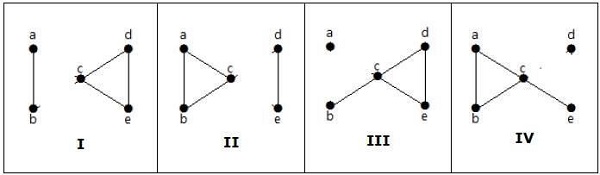
例子

以下哪些图是同构的？

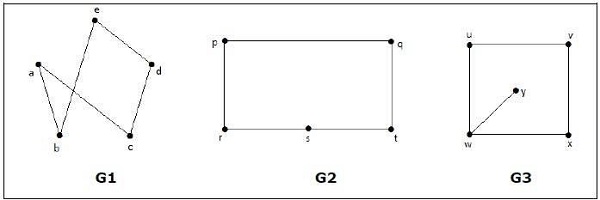
在图G₃中，顶点“w”的度数只有3，而所有其他图顶点的度数都为2。因此，G3与G₁或G₂不同构。

取G₁和G₂的补图，我们有：

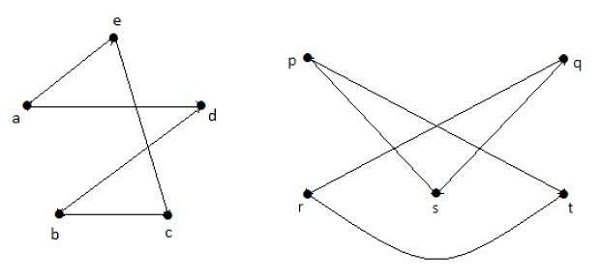
这里，(G₁− ≡ G₂−)，因此 (G₁ ≡ G₂)。

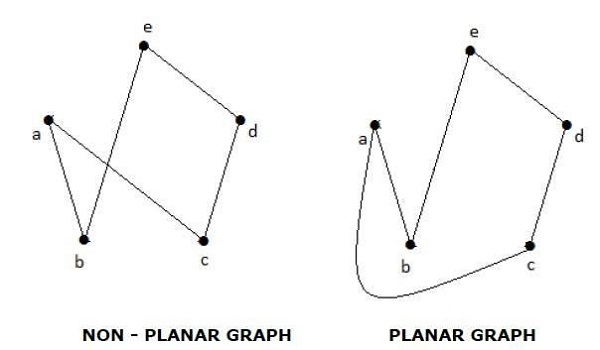
平面图

如果一个图“G”可以在平面上或球面上绘制，使得没有两条边在非顶点处相交，则称该图“G”为平面图。

例子

区域

每个平面图都将平面划分为称为区域的连通区域。

例子

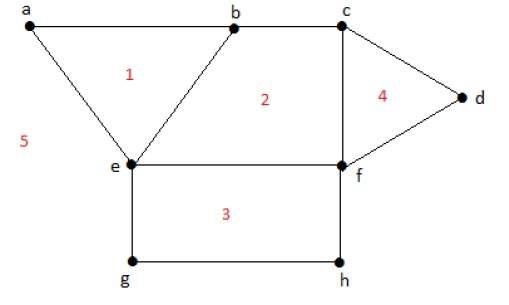
有界区域的度数r = deg(r) = 包围区域r的边的数量。

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8

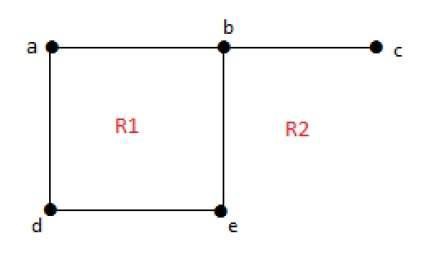
无界区域的度数r = deg(r) = 包围区域r的边的数量。

deg(R₁) = 4
deg(R₂) = 6

在平面图中，以下性质成立：

在一个具有“n”个顶点的平面图中，所有顶点的度数之和为：

n Σ i=1 deg(V_i) = 2|E|

根据区域度数之和/定理，在一个具有“n”个区域的平面图中，区域度数之和为：

n Σ i=1 deg(ri) = 2|E|

基于上述定理，您可以得出以下结论：

在一个平面图中，

如果每个区域的度数为K，则区域度数之和为：

K|R| = 2|E|

如果每个区域的度数至少为K(≥ K)，则

K|R| ≤ 2|E|

如果每个区域的度数最多为K(≤ K)，则

K|R| ≥ 2|E|

注意 − 假设所有区域的度数相同。

根据平面图上的欧拉公式，

如果一个图“G”是连通平面图，则

|V| + |R| = |E| + 2

如果一个平面图有“K”个分量，则

|V| + |R|=|E| + (K+1)

其中，|V| 是顶点数，|E| 是边数，|R| 是区域数。

边顶点不等式

如果“G”是一个连通平面图，每个区域的度数至少为“K”，则

|E| ≤ k / (k-2) {|v| - 2}

我们知道，|V| + |R| = |E| + 2

K.|R| ≤ 2|E|

K(|E| - |V| + 2) ≤ 2|E|

(K - 2)|E| ≤ K(|V| - 2)

|E| ≤ k / (k-2) {|v| - 2}

如果“G”是一个简单的连通平面图，则

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

至少存在一个顶点 V •∈ G，使得 deg(V) ≤ 5。

如果“G”是一个简单的连通平面图（至少有2条边）且没有三角形，则

|E| ≤ {2|V| – 4}

库拉托夫斯基定理

一个图“G”是非平面的当且仅当“G”具有一个与K₅或K_3,3同胚的子图。

同胚

如果可以通过用更多顶点划分G的一些边从同一个图“G”获得这两个图中的每一个，则称两个图G₁和G₂是同胚的。看下面的例子：

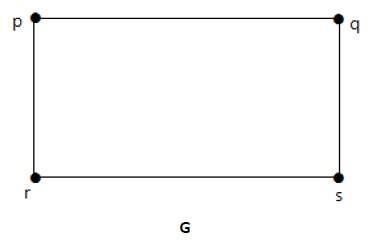
通过添加一个顶点将边“rs”分成两条边。

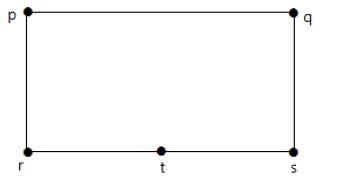
下面显示的图与第一个图同胚。

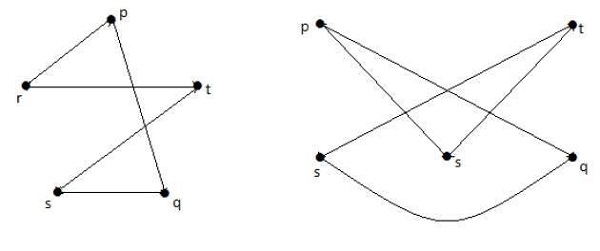
如果G₁与G₂同构，则G与G2同胚，但反过来不一定成立。

任何具有4个或更少顶点的图都是平面图。
任何具有8条或更少边的图都是平面图。
完全图K_n是平面图当且仅当n ≤ 4。
完全二部图K_{m, n}是平面图当且仅当m ≤ 2或n ≤ 2。
具有最小顶点数的简单非平面图是完全图K₅。
具有最小边数的简单非平面图是K_{3, 3}。

多面体图

如果每个顶点的度数≥ 3，即deg(V) ≥ 3 ∀ V ∈ G，则称简单的连通平面图为多面体图。

3|V| ≤ 2|E|
3|R| ≤ 2|E|

图论 - 可遍历性

如果您可以绘制一条路径连接所有顶点而无需回溯同一条路径，则该图是可遍历的。基于此路径，本章中描述了一些类别，例如欧拉路径和欧拉回路。

欧拉路径

欧拉路径恰好包含“G”的每条边一次，并且至少包含“G”的每个顶点一次。如果连通图G包含欧拉路径，则称该图是可遍历的。

例子

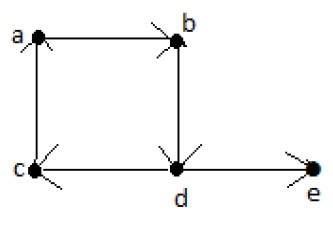
欧拉路径 = d-c-a-b-d-e。

欧拉回路

在欧拉路径中，如果起点与终点相同，则称为欧拉回路。

例子

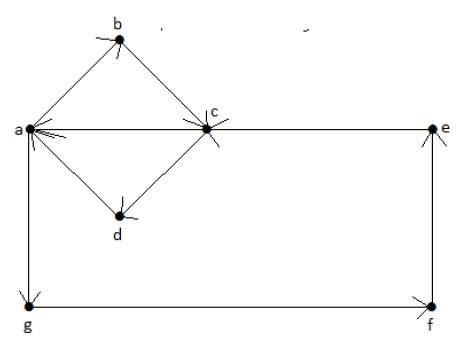
欧拉路径 = a-b-c-d-a-g-f-e-c-a。

欧拉回路定理

一个连通图“G”是可遍历的当且仅当G中具有奇数度的顶点数恰好为2或0。如果一个连通图G恰好有两个奇数度顶点，则它可以包含欧拉路径，但不能包含欧拉回路。

注意 − 此欧拉路径以奇数度顶点开始，以另一个奇数度顶点结束。

例子

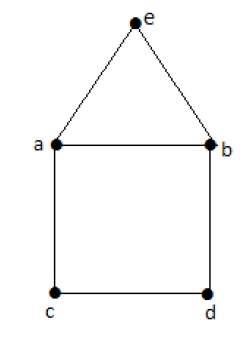
欧拉路径 − b-e-a-b-d-c-a 不是欧拉回路，但它是欧拉路径。显然它恰好有两个奇数度顶点。

注意 − 在连通图G中，如果具有奇数度的顶点数 = 0，则存在欧拉回路。

哈密顿图

如果存在一个包含G的所有顶点的环，则称连通图G为哈密顿图。

每个环都是回路，但回路可能包含多个环。这样的环称为G的哈密顿环。

哈密顿路径

如果一个连通图恰好包含G的每个顶点一次，则称该图是哈密顿图。这样的路径称为哈密顿路径。

例子

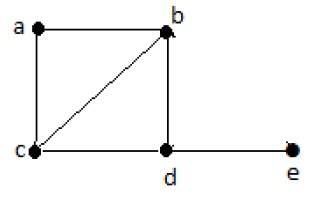
哈密顿路径− e-d-b-a-c。

注意

欧拉回路恰好包含图的每条边一次。
在哈密顿环中，可以跳过图的某些边。

例子

请看下面的图：

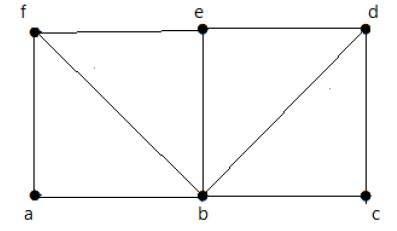
对于上面显示的图：

存在欧拉路径 – 否
存在欧拉回路 – 否
存在哈密顿环 – 是
存在哈密顿路径 – 正确

G 有四个奇数度顶点，因此它不可遍历。通过跳过内部边，该图具有一个经过所有顶点的哈密顿环。

图论 - 例子

本章将介绍一些标准示例，以演示我们在前面章节中已经讨论过的概念。

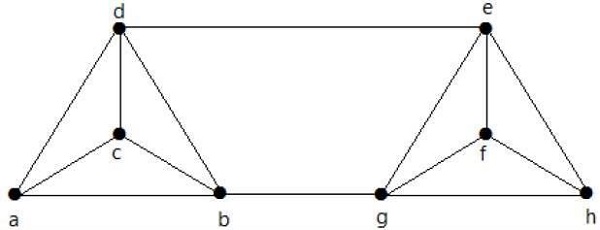
示例1

求下列图中生成树的个数。

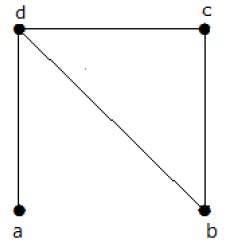
解答

从上图获得的生成树个数为 3。它们如下所示：

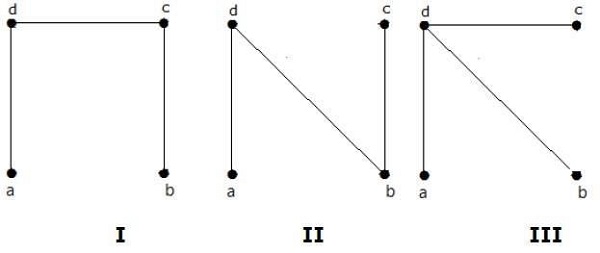
这三个是给定图的生成树。这里图 I 和图 II 彼此同构。显然，非同构生成树的个数为两个。

示例2

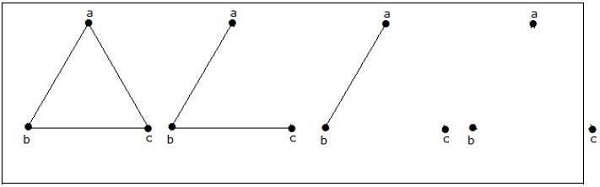
用 3 个顶点可以构成多少个简单的非同构图？

解答

用 3 个顶点可以构成 4 个非同构图。它们如下所示。

例 3

设‘G’是一个具有 20 个顶点的连通平面图，每个顶点的度数为 3。求该图中区域的个数。

解答

根据度数和定理，

20 Σ i=1 deg(Vi) = 2|E|

20(3) = 2|E|

|E| = 30

根据欧拉公式，

|V| + |R| = |E| + 2

20+ |R| = 30 + 2

|R| = 12

因此，区域个数为 12。

例 4

完全图 K_n 的色数是多少？

解答

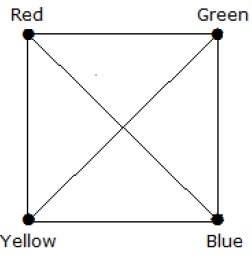
在完全图中，每个顶点都与其余 (n–1) 个顶点相邻。因此，每个顶点都需要一种新的颜色。因此，完全图 K_n 的色数 = n。

例 5

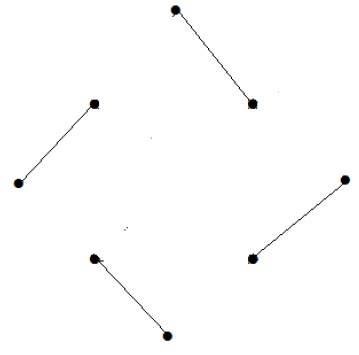
下列图的匹配数是多少？

解答

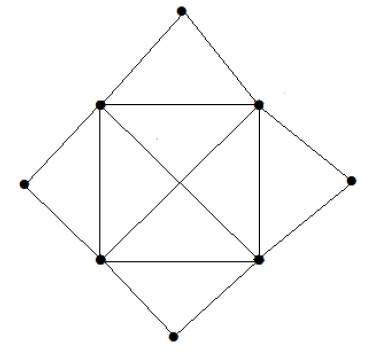
顶点数 = 9

我们只能匹配 8 个顶点。

匹配数为 4。

例 6

下列图的边覆盖数是多少？

解答

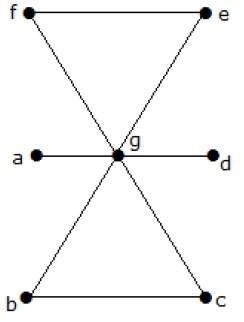
顶点数 = |V| = n = 7

边覆盖数 = (α₁) ≥ [n/2] = 3

α₁ ≥ 3

使用 3 条边，我们可以覆盖所有顶点。

因此，边覆盖数为 3。

打印页面