图论 - 例子

---

---

在本章中，我们将介绍一些标准示例，以演示我们在前面章节中已经讨论的概念。

示例 1

求以下图中生成树的个数。

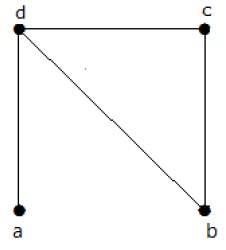
解答

从上图得到的生成树个数为 3。它们如下所示：

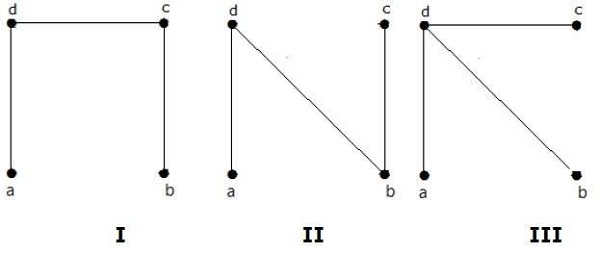
这三个是给定图的生成树。这里图 I 和 II 彼此同构。显然，非同构生成树的个数为两个。

示例 2

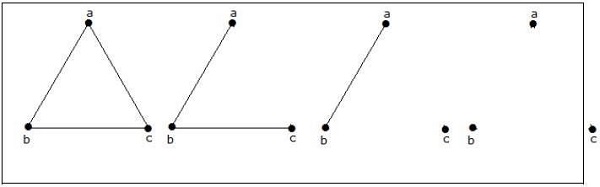
3 个顶点可能有多少个简单的非同构图？

解答

3 个顶点可能存在 4 个非同构图。它们如下所示。

示例 3

设“G”是一个具有 20 个顶点的连通平面图，每个顶点的度数为 3。求图中区域的个数。

解答

根据度数和定理，

20 Σ i=1 deg(Vi) = 2|E|

20(3) = 2|E|

|E| = 30

根据欧拉公式，

|V| + |R| = |E| + 2

20+ |R| = 30 + 2

|R| = 12

因此，区域的个数为 12。

示例 4

完全图 K_n 的色数是多少？

解答

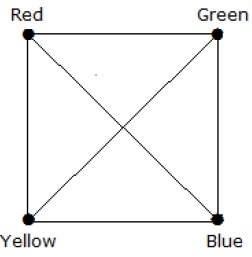
在完全图中，每个顶点都与其余 (n–1) 个顶点相邻。因此，每个顶点都需要一个新的颜色。因此，完全图 K_n 的色数为 n。

示例 5

以下图的匹配数是多少？

解答

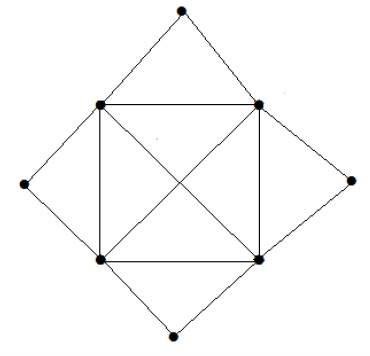
顶点数 = 9

我们只能匹配 8 个顶点。

匹配数为 4。

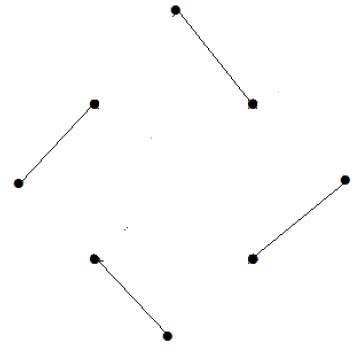
示例 6

以下图的边覆盖数是多少？

解答

顶点数 = |V| = n = 7

边覆盖数 = (α₁) ≥ [n/2] = 3

α₁ ≥ 3

使用 3 条边，我们可以覆盖所有顶点。

因此，边覆盖数为 3。