图论 - 匹配

---

---

匹配图是图的一个子图，其中没有边彼此相邻。简单来说，任意两条边之间不应该有任何公共顶点。

匹配

设‘G’ = (V, E) 为一个图。如果G的每个顶点最多与M中的一条边关联，则子图称为匹配M(G)，即：

deg(V) ≤ 1 ∀ V ∈ G

这意味着在匹配图M(G)中，顶点的度数应为1或0，其中边应来自图G。

符号 − M(G)

示例

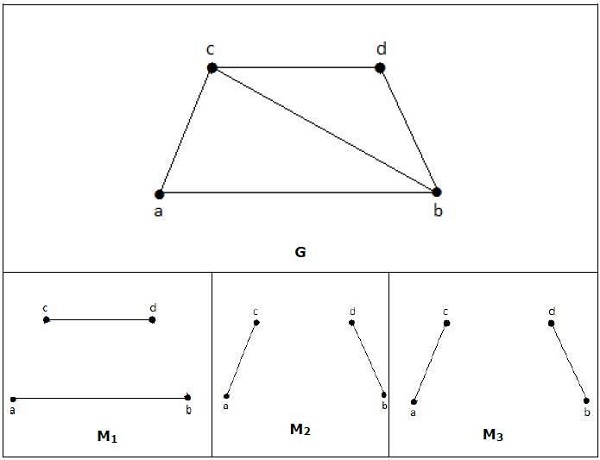
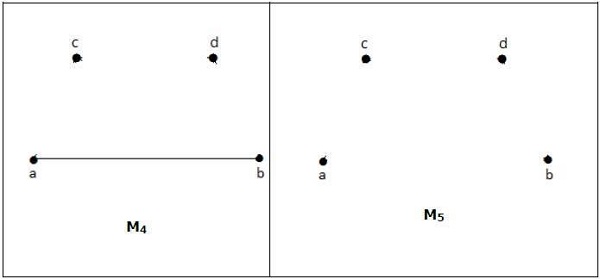
在匹配中：

如果deg(V) = 1，则(V)被称为匹配的

如果deg(V) = 0，则(V)未匹配。

在匹配中，任意两条边不相邻。这是因为如果任意两条边相邻，则连接这两条边的顶点的度数将为2，这违反了匹配规则。

最大匹配

如果不能将图‘G’的任何其他边添加到M中，则称图‘G’的匹配M为最大匹配。

示例

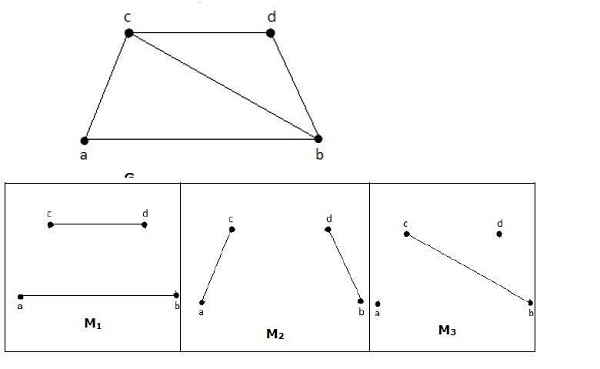
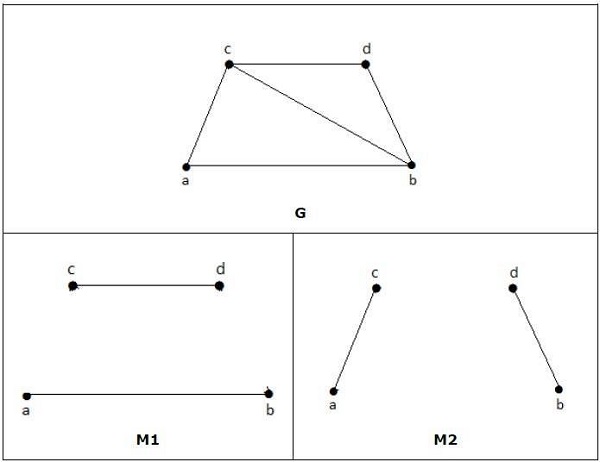
上图中的M1、M2、M3是G的最大匹配。

最大匹配

也称为最大最大匹配。最大匹配定义为具有最大边数的最大匹配。

‘G’的最大匹配中的边数称为其匹配数。

示例

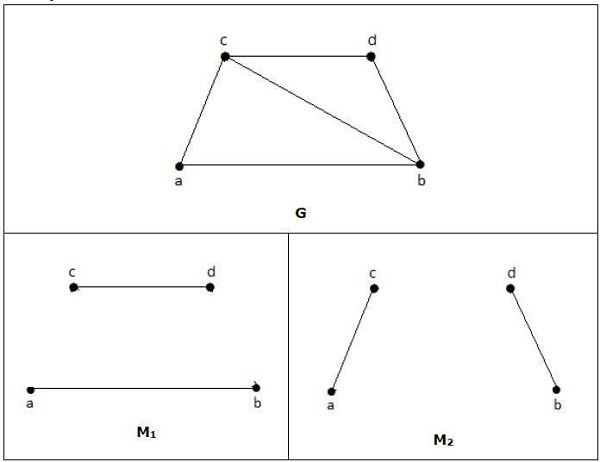
对于上面示例中给出的图，M1和M2是‘G’的最大匹配，其匹配数为2。因此，使用图G，我们最多只能形成只有2条边的子图。因此，匹配数为二。

完美匹配

如果图g (G)的每个顶点都恰好与匹配(M)的一条边关联，则称图(G)的匹配(M)为完美匹配，即：

deg(V) = 1 ∀ V

子图中每个顶点的度数都应为1。

示例

在下图中，M1和M2是G的完美匹配的例子。

注意 − 图的每个完美匹配也是图的最大匹配，因为在完美匹配图中没有机会再添加一条边。

图的最大匹配不一定是完美的。如果图‘G’有一个完美匹配，则顶点数|V(G)|为偶数。如果是奇数，则最后一个顶点与另一个顶点配对，最终剩下一个单一顶点，它不能与任何其他顶点配对，其度数为零。这显然违反了完美匹配原则。

示例

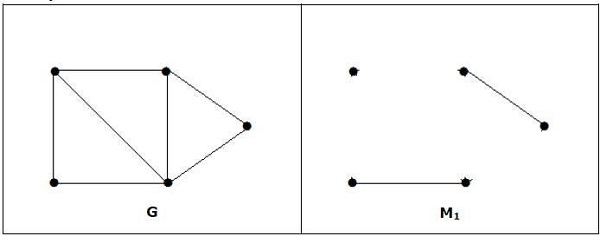
注意 − 上述陈述的逆命题不一定为真。如果G的顶点数为偶数，则M1不必是完美的。

示例

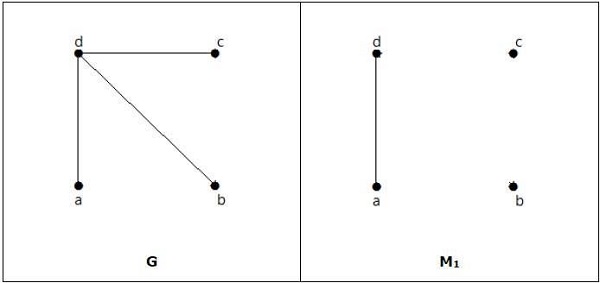
它是匹配，但即使它有偶数个顶点，它也不是完美匹配。