广度优先搜索 (BFS)

图是对象集合的一种图形表示，其中某些对象对通过链接连接。相互连接的对象由称为顶点的点表示，连接顶点的链接称为边。

正式地，图是一对集合(V, E)，其中V是顶点集，E是连接顶点对的边集。请看下面的图 -

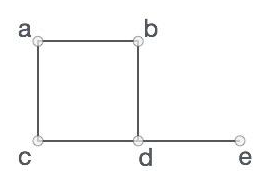
在上图中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

广度优先搜索 (BFS)

广度优先搜索 (BFS) 算法以广度优先的方式遍历图，并使用队列来记住在任何迭代中遇到死胡同时，下一个要开始搜索的顶点。

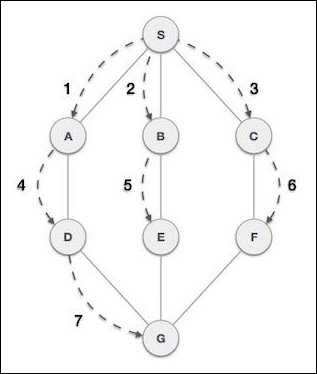
如上例所示，BFS 算法首先从 A 到 B 到 E 到 F，然后到 C 和 G，最后到 D。它采用以下规则。

• 规则 1 - 访问相邻的未访问顶点。将其标记为已访问。显示它。将其插入队列。

• 规则 2 - 如果未找到相邻顶点，则从队列中删除第一个顶点。

• 规则 3 - 重复规则 1 和规则 2，直到队列为空。

步骤	遍历	描述
1		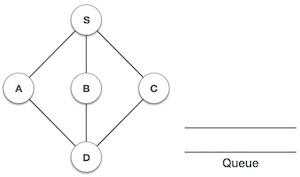初始化队列。
2		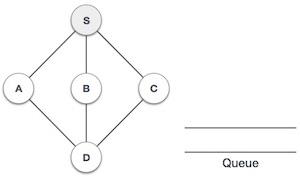我们从访问S（起始节点）开始，并将其标记为已访问。
3		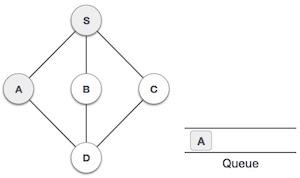然后我们从S看到一个未访问的相邻节点。在本例中，我们有三个节点，但按字母顺序我们选择A，将其标记为已访问并将其入队。
4		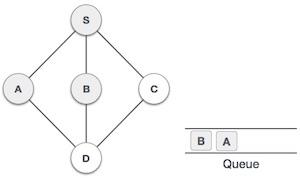接下来，S的未访问相邻节点是B。我们将其标记为已访问并将其入队。
5		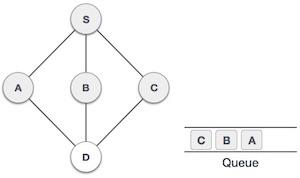接下来，S的未访问相邻节点是C。我们将其标记为已访问并将其入队。
6		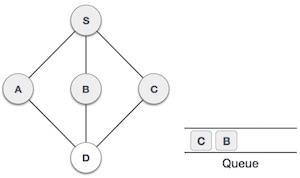现在，S没有未访问的相邻节点了。因此，我们出队并找到A。
7		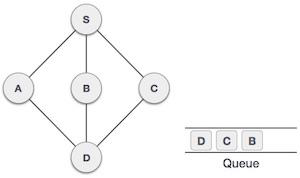从A我们有D作为未访问的相邻节点。我们将其标记为已访问并将其入队。

在这个阶段，我们没有未标记（未访问）的节点了。但根据算法，我们继续出队以获取所有未访问的节点。当队列清空时，程序结束。