最短路径算法
最短路径算法是一种找到从源节点 (S) 到目标节点 (D) 的最低成本路径的方法。在这里,我们将讨论 Moore 算法,也称为广度优先搜索算法。
Moore 算法
标记源顶点 S 并将其标记为 i 并设置 i = 0。
找到与标记为 i 的顶点相邻的所有未标记的顶点。如果没有任何顶点连接到顶点 S,则顶点 D 未连接到 S。如果存在连接到 S 的顶点,则将其标记为 i+1。
如果 D 已标记,则转到步骤 4,否则转到步骤 2 以增加 i = i+1。
找到最短路径的长度后停止。
Dijkstra 算法
Dijkstra 算法解决了有向加权图 G = (V, E) 上的单源最短路径问题,其中所有边的权重均为非负数(即对于每条边 (u, v) Є E),w(u, v) ≥ 0)。
在以下算法中,我们将使用一个函数 Extract-Min(),它提取具有最小键的节点。
算法:Dijkstra-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
S := Ф
Q := G.V
while Q ≠ Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v.∏ := u
分析
该算法的复杂度完全取决于 Extract-Min 函数的实现。如果使用线性搜索实现 Extract-Min 函数,则该算法的复杂度为 O(V2 + E)。
在此算法中,如果我们使用最小堆,Extract-Min() 函数在该堆上工作以从 Q 返回具有最小键的节点,则可以进一步降低该算法的复杂度。
示例
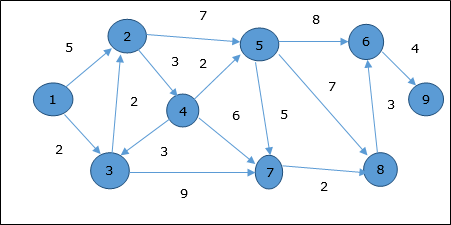
让我们考虑顶点 1 和 9 分别作为起点和终点。最初,除起点外的所有顶点均标记为 ∞,起点标记为 0。
| 顶点 | 初始 | 步骤 1 V1 | 步骤 2 V3 | 步骤 3 V2 | 步骤 4 V4 | 步骤 5 V5 | 步骤 6 V7 | 步骤 7 V8 | 步骤 8 V6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
因此,顶点 9 与顶点 1 之间的最小距离为 20。路径为
1 → 3 → 7 → 8 → 6 → 9
此路径是根据前驱信息确定的。
Bellman-Ford 算法
该算法解决了有向图 G = (V, E) 的单源最短路径问题,其中边权重可能为负数。此外,如果不存在任何负权重循环,则可以应用此算法来查找最短路径。
算法:Bellman-Ford-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v.∏ := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
分析
第一个 for 循环用于初始化,运行 O(V) 次。下一个 for 循环在边上运行 |V - 1| 次,需要 O(E) 次。
因此,Bellman-Ford 算法在 O(V, E) 时间内运行。
示例
以下示例逐步显示 Bellman-Ford 算法的工作原理。该图具有负边,但没有任何负循环,因此可以使用此技术解决问题。
在初始化时,除源节点外的所有顶点均标记为 ∞,源节点标记为 0。
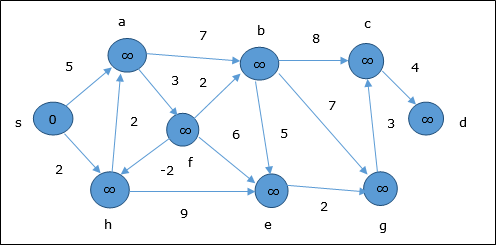
在第一步中,所有可从源节点到达的顶点都将更新为最小成本。因此,顶点 a 和 h 会更新。
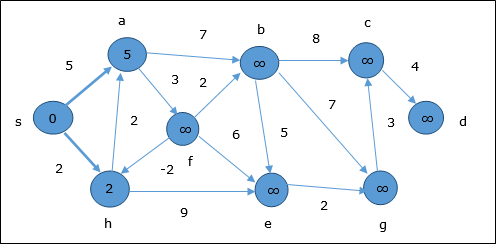
在下一步中,顶点 a, b, f 和 e 会更新。
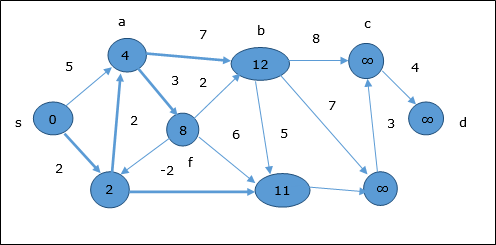
遵循相同的逻辑,在此步骤中,顶点 b, f, c 和 g 会更新。
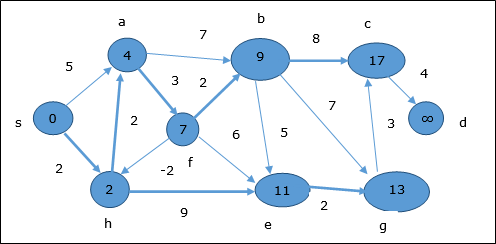
在这里,顶点 c 和 d 会更新。
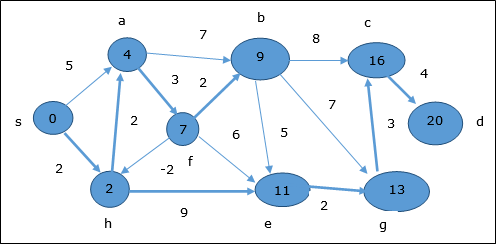
因此,顶点 s 和顶点 d 之间的最小距离为 20。
根据前驱信息,路径为 s → h → e → g → c → d
