Java 数据结构 - 快速指南
Java 数据结构 - 创建数组
在 Java 中,数组是一种数据结构/容器,它存储相同类型元素的固定大小的顺序集合。数组用于存储数据集合,但通常将数组视为相同类型变量的集合更有用。
元素 - 存储在数组中的每个项目称为元素。
索引 - 数组中每个元素的位置都有一个数字索引,用于标识元素。
创建数组
要创建数组,需要声明特定的数组,指定其类型和引用它的变量。然后,使用 new 运算符为已声明的数组分配内存(在方括号“[ ]”中指定数组的大小)。
语法
dataType[] arrayRefVar; arrayRefVar = new dataType[arraySize]; (or) dataType[] arrayRefVar = new dataType[arraySize];
或者,您可以通过直接指定用逗号分隔的元素来创建数组,这些元素位于花括号“{ }”内。
dataType[] arrayRefVar = {value0, value1, ..., valuek};
通过索引访问数组元素。数组索引是从 0 开始的;也就是说,它们从 0 开始到 arrayRefVar.length-1。
示例
以下语句声明一个整数类型的数组变量 myArray,并分配内存以存储 10 个整数类型元素并将它的引用赋值给 myArray。
int[] myList = new int[10];
填充数组
上面的语句只是创建了一个空数组。需要通过使用索引为每个位置赋值来填充此数组 -
myList [0] = 1; myList [1] = 10; myList [2] = 20; . . . .
示例
以下是一个 Java 示例,用于创建一个整数数组。在这个例子中,我们尝试创建一个大小为 10 的整数数组,填充它,并使用循环显示它的内容。
public class CreatingArray {
public static void main(String args[]) {
int[] myArray = new int[10];
myArray[0] = 1;
myArray[1] = 10;
myArray[2] = 20;
myArray[3] = 30;
myArray[4] = 40;
myArray[5] = 50;
myArray[6] = 60;
myArray[7] = 70;
myArray[8] = 80;
myArray[9] = 90;
System.out.println("Contents of the array ::");
for(int i = 0; i<myArray.length; i++) {
System.out.println("Element at the index "+i+" ::"+myArray[i]);
}
}
}
输出
Contents of the array :: Element at the index 0 ::1 Element at the index 1 ::10 Element at the index 2 ::20 Element at the index 3 ::30 Element at the index 4 ::40 Element at the index 5 ::50 Element at the index 6 ::60 Element at the index 7 ::70 Element at the index 8 ::80 Element at the index 9 ::90
示例
以下是另一个 Java 示例,它通过获取用户的输入来创建和填充数组。
import java.util.Scanner;
public class CreatingArray {
public static void main(String args[]) {
// Instantiating the Scanner class
Scanner sc = new Scanner(System.in);
// Taking the size from user
System.out.println("Enter the size of the array ::");
int size = sc.nextInt();
// creating an array of given size
int[] myArray = new int[size];
// Populating the array
for(int i = 0 ;i<size; i++) {
System.out.println("Enter the element at index "+i+" :");
myArray[i] = sc.nextInt();
}
// Displaying the contents of the array
System.out.println("Contents of the array ::");
for(int i = 0; i<myArray.length; i++) {
System.out.println("Element at the index "+i+" ::"+myArray[i]);
}
}
}
输出
Enter the size of the array :: 5 Enter the element at index 0 : 25 Enter the element at index 1 : 65 Enter the element at index 2 : 78 Enter the element at index 3 : 66 Enter the element at index 4 : 54 Contents of the array :: Element at the index 0 ::25 Element at the index 1 ::65 Element at the index 2 ::78 Element at the index 3 ::66 Element at the index 4 ::54
向数组插入元素
插入操作是将一个或多个数据元素插入数组中。根据需要,可以在数组的开头、结尾或任何给定索引处添加新元素。
算法
令LA为具有N个元素的线性数组(无序),K为正整数,使得K<=N。以下是将ITEM插入到LA的第K个位置的算法 -
Step 1 - Start Step 2 - Set J = N Step 3 - Set N = N+1 Step 4 - Repeat steps 5 and 6 while J >= K Step 5 - Set LA[J+1] = LA[J] Step 6 - Set J = J-1 Step 7 - Set LA[K] = ITEM Step 8 - Stop
示例
由于 Java 中的数组大小在插入操作后是固定的,因此不会显示数组的冗余元素。因此,如果您在数组中间插入元素,为了显示最后一个元素,需要创建一个大小为 n+1 的新数组(其中 n 是当前数组的大小),并将元素插入其中,然后显示它,或者在打印数组内容后单独打印最后一个元素。
public class InsertingElements {
public static void main(String args[]) {
int[] myArray = {10, 20, 30, 45, 96, 66};
int pos = 3;
int data = 105;
int j = myArray.length;
int lastElement = myArray[j-1];
for(int i = (j-2); i >= (pos-1); i--) {
myArray[i+1] = myArray[i];
}
myArray[pos-1] = data;
System.out.println("Contents of the array after insertion ::");
for(int i = 0; i < myArray.length; i++) {
System.out.print(myArray[i]+ ", ");
}
System.out.print(lastElement);
}
}
输出
Contents of the array after insertion :: 10, 20, 105, 30, 45, 96, 66
Apache Commons 提供了一个名为org.apache.commons.lang3的库,以下是将库添加到项目的 Maven 依赖项。
<dependencies>
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-lang3</artifactId>
<version>3.0</version>
</dependency>
</dependencies>
此包提供了一个名为ArrayUtils的类。您可以使用此类的add()方法在数组的特定位置添加元素。
示例
import java.util.Scanner;
import org.apache.commons.lang3.ArrayUtils;
public class InsertingElements {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of elements needed :");
int n = sc.nextInt();
int[] myArray = new int[n];
System.out.println("Enter the elements ::");
for(int i = 0; i < n; i++) {
myArray[i] = sc.nextInt();
}
System.out.println("Enter the position to insert the element :");
int pos = sc.nextInt();
System.out.println("Enter the element:");
int element = sc.nextInt();
int [] result = ArrayUtils.add(myArray, pos, element);
System.out.println("Contents of the array after insertion ::");
for(int i = 0; i < result.length; i++) {
System.out.print(result[i]+ " ");
}
}
}
输出
Enter the number of elements needed : 5 Enter the elements :: 55 45 25 66 45 Enter the position to insert the element : 3 Enter the element: 404 Contents of the array after insertion :: 55 45 25 404 66 45
从数组中删除元素
要从数组中删除现有元素,需要跳过给定位置(例如 k)处的元素,方法是用下一个元素 (k+1) 替换它,然后用 k+2 处的元素替换 k+1 处的元素,一直持续到数组的末尾。最后忽略最后一个元素。
算法
假设 LA 是一个具有 N 个元素的线性数组,K 是一个正整数,使得 K<=N。以下是删除 LA 的第 K 个位置的元素的算法。
Step 1 - Start Step 2 - Set J = K Step 3 - Repeat steps 4 and 5 while J < N Step 4 - Set LA[J] = LA[J + 1] Step 5 - Set J = J+1 Step 6 - Set N = N-1 Step 7 - Stop
示例
public class RemovingElements {
public static void main(String args[]) {
int[] myArray = {10, 20, 30, 45, 96, 66};
int pos = 3;
int j = myArray.length;
for(int i = pos; i < j-1; i++) {
myArray[i] = myArray[i+1];
}
System.out.println("Contents of the array after deletion ::");
for(int i = 0; i < myArray.length-1; i++) {
System.out.print(myArray[i]+ ", ");
}
}
}
输出
Contents of the array after deletion :: 10, 20, 30, 96, 66,
ArrayUtils类提供remove()方法来从数组中删除元素。
示例
import java.util.Scanner;
import org.apache.commons.lang3.ArrayUtils;
public class RemovingElements {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of elements needed :");
int n = sc.nextInt();
int[] myArray = new int[n];
System.out.println("Enter the elements ::");
for(int i = 0; i < n; i++) {
myArray[i] = sc.nextInt();
}
System.out.println("Enter the position to delete the element :");
int pos = sc.nextInt();
int [] result = ArrayUtils.remove(myArray, pos);
System.out.println("Contents of the array after deletion ::");
for(int i = 0; i < result.length; i++) {
System.out.print(result[i]+ " ");
}
}
}
输出
Enter the number of elements needed : 5 Enter the elements :: 44 55 62 45 55 Enter the position to delete the element : 3 Contents of the array after deletion :: 44 55 62 55
Java 数据结构 - 合并两个数组
一种方法是创建一个长度等于两个数组长度之和的数组,然后逐个将两个数组的元素添加到其中。
示例
import java.util.Arrays;
public class JoiningTwoArrays {
public static void main(String args[]) {
String[] arr1 = {"JavaFX", "OpenNLP", "OpenCV", "Java"};
String[] arr2 = {"Hadoop", "Sqoop", "HBase", "Hive" };
String[] result = new String[arr1.length+arr2.length];
int count = 0;
for(int i = 0; i<arr1.length; i++ ) {
result[i] = arr1[i];
count++;
}
for(int i = 0; i<arr2.length; i++ ) {
result[count++] = arr2[i];
}
System.out.println("Contents of the resultant array ::");
System.out.println(Arrays.toString(result));
}
}
输出
Contents of the resultant array :: [JavaFX, OpenNLP, OpenCV, Java, Hadoop, Sqoop, HBase, Hive]
排序数组元素
要对数组进行排序,请按照以下步骤操作。
比较数组的前两个元素
如果第一个元素大于第二个元素,则交换它们。
然后,比较第二个和第三个元素,如果第二个元素大于第三个元素,则交换它们。
重复此操作直到数组结束。
交换数组
创建一个变量 (temp),将其初始化为 0。
将第一个数字赋值给 temp。
将第二个数字赋值给第一个数字。
将 temp 赋值给第二个数字。
示例
import java.util.Arrays;
public class SortingArray {
public static void main(String args[]) {
// String[] myArray = {"JavaFX", "HBase", "OpenCV", "Java", "Hadoop", "Neo4j"};
int[] myArray = {2014, 2545, 4236, 6521, 1254, 2455, 5756, 66406};
int size = myArray.length;
for(int i = 0; i<size-1; i++) {
for (int j = i+1; j<size; j++) {
if(myArray[i]>(myArray[j])) {
int temp = myArray[i];
myArray[i] = myArray[j];
myArray[j] = temp;
}
}
}
System.out.println("Sorted array :"+Arrays.toString(myArray));
}
}
输出
Sorted array :[1254, 2014, 2455, 2545, 4236, 5756, 6521, 66406]
在数组中搜索元素
您可以使用几种算法搜索数组的元素,在此实例中,让我们讨论线性搜索算法。
线性搜索是一种非常简单的搜索算法。在这种类型的搜索中,会对所有项目逐个进行顺序搜索。检查每个项目,如果找到匹配项,则返回该特定项目,否则搜索将继续到数据集合的末尾。
算法
Step 1 - Set i to 1. Step 2 - if i > n then go to step 7. Step 3 - if A[i] = x then go to step 6. Step 4 - Set i to i + 1. Step 5 - Go to Step 2. Step 6 - Print Element x Found at index i and go to step 8. Step 7 - Print element not found.
程序
public class LinearSearch {
public static void main(String args[]) {
int array[] = {10, 20, 25, 63, 96, 57};
int size = array.length;
int value = 63;
for (int i = 0 ; i < size-1; i++) {
if(array[i]==value) {
System.out.println("Index of the required element is :"+ i);
}
}
}
}
输出
Index of the required element is :3
二维数组
Java 中的二维数组表示为相同类型的一维数组的数组。它主要用于表示具有行和列的值表 -
Int[][] myArray = {{10, 20, 30}, {11, 21, 31}, {12, 22, 32} }
简而言之,二维数组包含一维数组作为元素。它由两个索引表示,其中第一个索引表示数组的位置,第二个索引表示该特定数组中元素的位置 -
示例
public class Creating2DArray {
public static void main(String args[]) {
int[][] myArray = new int[3][3];
myArray[0][0] = 21;
myArray[0][1] = 22;
myArray[0][2] = 23;
myArray[1][0] = 24;
myArray[1][1] = 25;
myArray[1][2] = 26;
myArray[2][0] = 27;
myArray[2][1] = 28;
myArray[2][2] = 29;
for(int i = 0; i<myArray.length; i++ ) {
for(int j = 0;j<myArray.length; j++) {
System.out.print(myArray[i][j]+" ");
}
System.out.println();
}
}
}
输出
21 22 23 24 25 26 27 28 29
Java 数据结构 - 遍历数组
为了处理数组元素,我们经常使用 for 循环或 for each 循环,因为数组中的所有元素都是相同类型,并且数组的大小是已知的。假设我们有一个包含 5 个元素的数组,我们可以打印此数组的所有元素,如下所示 -
示例
public class ProcessingArrays {
public static void main(String args[]) {
int myArray[] = {22, 23, 25, 27, 30};
for(int i = 0; i<myArray.length; i++) {
System.out.println(myArray[i]);
}
}
}
输出
22 23 25 27 30
Java 数据结构 - BitSet 类
BitSet 类创建一种特殊类型的数组,用于保存位值。它可以根据需要增加大小,这使其类似于位向量。BitSet 的索引由非负值表示,每个索引都保存一个布尔值。
Java 中的 BitSet 类
BitSet 类实现一组位或标志,可以单独设置和清除。当您需要跟踪一组布尔值时,此类非常有用;您只需为每个值分配一个位,并根据需要设置或清除它。BitSet 数组可以根据需要增加大小。这使其类似于位向量。
BitSet 定义了以下两个构造函数。
| 序号 | 构造函数和描述 |
|---|---|
| 1 | BitSet( ) 此构造函数创建一个默认对象。 |
| 2 | BitSet(int size) 此构造函数允许您指定其初始大小,即它可以容纳的位数。所有位都初始化为零。 |
BitSet 实现 Cloneable 接口并定义下表中列出的方法
| 序号 | 方法和描述 |
|---|---|
| 1 | void and(BitSet bitSet) 将调用 BitSet 对象的内容与 bitSet 指定的内容进行 AND 运算。结果将放入调用对象中。 |
| 2 | void andNot(BitSet bitSet) 对于 bitSet 中的每个 1 位,调用 BitSet 中的相应位将被清除。 |
| 3 | int cardinality( ) 返回调用对象中已设置位的数量。 |
| 4 | void clear( ) 将所有位清零。 |
| 5 | void clear(int index) 将索引指定的位清零。 |
| 6 | void clear(int startIndex, int endIndex) 将从startIndex到endIndex的位清零。 |
| 7 | Object clone( ) 复制调用 BitSet 对象。 |
| 8 | boolean equals(Object bitSet) 如果调用的位集与bitSet中传入的位集等效,则返回true。否则,方法返回false。 |
| 9 | void flip(int index) 反转索引指定的位。 |
| 10 | void flip(int startIndex, int endIndex) 反转从startIndex到endIndex的位。 |
| 11 | boolean get(int index) 返回指定索引处位的当前状态。 |
| 12 | BitSet get(int startIndex, int endIndex) 返回一个由startIndex到endIndex的位组成的BitSet。调用对象不会改变。 |
| 13 | int hashCode( ) 返回调用对象的哈希码。 |
| 14 | boolean intersects(BitSet bitSet) 如果调用对象和bitSet中至少有一对对应的位为1,则返回true。 |
| 15 | boolean isEmpty( ) 如果调用对象中的所有位都为零,则返回true。 |
| 16 | int length( ) 返回保存调用BitSet内容所需的位数。此值由最后一位1的位置确定。 |
| 17 | int nextClearBit(int startIndex) 返回下一个已清除位(即下一个零位)的索引,从startIndex指定的索引开始。 |
| 18 | int nextSetBit(int startIndex) 返回下一个已设置位(即下一个1位)的索引,从startIndex指定的索引开始。如果没有设置位,则返回-1。 |
| 19 | void or(BitSet bitSet) 将调用BitSet对象的内容与bitSet指定的内容进行按位或运算。结果将放入调用对象中。 |
| 20 | void set(int index) 设置索引指定的位。 |
| 21 | void set(int index, boolean v) 将索引指定的位设置为v中传入的值。True设置位,False清除位。 |
| 22 | void set(int startIndex, int endIndex) 设置从startIndex到endIndex的位。 |
| 23 | void set(int startIndex, int endIndex, boolean v) 将从startIndex到endIndex的位设置为v中传入的值。True设置位,False清除位。 |
| 24 | int size( ) 返回调用BitSet对象中的位数。 |
| 25 | String toString( ) 返回调用BitSet对象的字符串等效项。 |
| 26 | void xor(BitSet bitSet) 将调用BitSet对象的内容与bitSet指定的内容进行按位异或运算。结果将放入调用对象中。 |
示例
以下程序演示了此数据结构支持的几种方法
import java.util.BitSet;
public class BitSetDemo {
public static void main(String args[]) {
BitSet bits1 = new BitSet(16);
BitSet bits2 = new BitSet(16);
// set some bits
for(int i = 0; i < 16; i++) {
if((i % 2) == 0) bits1.set(i);
if((i % 5) != 0) bits2.set(i);
}
System.out.println("Initial pattern in bits1: ");
System.out.println(bits1);
System.out.println("\n Initial pattern in bits2: ");
System.out.println(bits2);
// AND bits
bits2.and(bits1);
System.out.println("\nbits2 AND bits1: ");
System.out.println(bits2);
// OR bits
bits2.or(bits1);
System.out.println("\nbits2 OR bits1: ");
System.out.println(bits2);
// XOR bits
bits2.xor(bits1);
System.out.println("\nbits2 XOR bits1: ");
System.out.println(bits2);
}
}
输出
Initial pattern in bits1:
{0, 2, 4, 6, 8, 10, 12, 14}
Initial pattern in bits2:
{1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14}
bits2 AND bits1:
{2, 4, 6, 8, 12, 14}
bits2 OR bits1:
{0, 2, 4, 6, 8, 10, 12, 14}
bits2 XOR bits1:
{}
Java数据结构 - 创建BitSet
可以通过实例化java.util包的BitSet类来创建一个BitSet。BitSet类的一个构造函数允许您指定其初始大小,即它可以容纳的位数。
因此,要创建一个位集,请通过将所需的位数传递给其构造函数来实例化BitSet类。
BitSet bitSet = new BitSet(5);
示例
import java.util.BitSet;
public class CreatingBitSet {
public static void main(String args[]) {
BitSet bitSet = new BitSet(5);
bitSet.set(0);
bitSet.set(2);
bitSet.set(4);
System.out.println(bitSet);
}
}
输出
{0, 2, 4}
向 BitSet 添加值
BitSet类提供set()方法,用于将指定位的true。
示例
import java.util.BitSet;
public class CreatingBitSet {
public static void main(String args[]) {
BitSet bitSet = new BitSet(5);
bitSet.set(0);
bitSet.set(2);
bitSet.set(4);
System.out.println(bitSet);
}
}
输出
{0, 2, 4}
从 BitSet 中删除元素
可以使用BitSet类的clear()方法清除所有位,即设置所有位为false。类似地,也可以通过将索引作为参数传递给此方法来清除所需索引处的值。
示例
以下是一个删除BitSet类元素的示例。这里,我们尝试将索引为偶数值(最多25)的元素设置为true。稍后我们将清除索引值为5的倍数的元素。
import java.util.BitSet;
public class RemovingelementsOfBitSet {
public static void main(String args[]) {
BitSet bitSet = new BitSet(10);
for (int i = 1; i<25; i++) {
if(i%2==0) {
bitSet.set(i);
}
}
System.out.println(bitSet);
System.out.println("After clearing the contents ::");
for (int i = 0; i<25; i++) {
if(i%5==0) {
bitSet.clear(i);
}
}
System.out.println(bitSet);
}
}
输出
{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
After clearing the contents ::
{2, 4, 6, 8, 12, 14, 16, 18, 22, 24}
验证 BitSet 是否为空
当其中的所有值都为false时,位集被认为为空。BitSet类提供isEmpty()方法。此方法返回一个布尔值,当当前BitSet为空时为false,不为空时为true。
可以使用isEmpty()方法验证特定的BitSet是否为空。
示例
import java.util.BitSet;
public class isEmpty {
public static void main(String args[]) {
BitSet bitSet = new BitSet(10);
for (int i = 1; i<25; i++) {
if(i%2==0) {
bitSet.set(i);
}
}
if (bitSet.isEmpty()) {
System.out.println("This BitSet is empty");
} else {
System.out.println("This BitSet is not empty");
System.out.println("The contents of it are : "+bitSet);
}
bitSet.clear();
if (bitSet.isEmpty()) {
System.out.println("This BitSet is empty");
} else {
System.out.println("This BitSet is not empty");
System.out.println("The contents of it are : "+bitSet);
}
}
}
输出
This BitSet is not empty
The contents of it are : {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
This BitSet is empty
打印 BitSet 的元素
BitSet类的get()方法返回指定索引处位的当前状态/值。使用它可以打印BitSet的内容。
示例
import java.util.BitSet;
public class PrintingElements {
public static void main(String args[]) {
BitSet bitSet = new BitSet(10);
for (int i = 1; i<25; i++) {
if(i%2==0) {
bitSet.set(i);
}
}
System.out.println("After clearing the contents ::");
for (int i = 1; i<=25; i++) {
System.out.println(i+": "+bitSet.get(i));
}
}
}
输出
After clearing the contents :: 1: false 2: true 3: false 4: true 5: false 6: true 7: false 8: true 9: false 10: true 11: false 12: true 13: false 14: true 15: false 16: true 17: false 18: true 19: false 20: true 21: false 22: true 23: false 24: true 25: false
或者,可以直接使用println()方法打印位集的内容。
System.out.println(bitSet);
Java数据结构 - Vector类
Vector是一种类似于数组的数据结构。像数组一样,它分配连续的内存。与栈不同,Vector的大小是灵活的。
Vector 类
java.util.Vector类实现了一个可增长的对象数组。类似于数组,它包含可以使用整数索引访问的组件。以下是关于Vector的重要几点:
Vector的大小可以根据需要增长或缩小以适应添加和删除项目。
每个向量都试图通过维护一个容量和一个容量增量来优化存储管理。
从Java 2平台v1.2开始,此类经过改造以实现List接口。
与新的集合实现不同,Vector是同步的。
此类是Java集合框架的成员。
类声明
以下是java.util.Vector类的声明:
public class Vector<E> extends AbstractList<E> implements List<E>, RandomAccess, Cloneable, Serializable
这里<E>表示一个元素,可以是任何类。例如,如果您正在构建一个整数的数组列表,那么您可以按如下方式初始化它:
ArrayList<Integer> list = new ArrayList<Integer>();
类构造函数
| 序号 | 构造函数和描述 |
|---|---|
| 1 | Vector() 此构造函数用于创建一个空向量,以便其内部数据数组的大小为10,其标准容量增量为零。 |
| 2 | Vector(Collection<? extends E> c) 此构造函数用于创建一个包含指定集合元素的向量,其顺序与集合的迭代器返回的顺序相同。 |
| 3 | Vector(int initialCapacity) 此构造函数用于创建一个具有指定初始容量且容量增量等于零的空向量。 |
| 4 | Vector(int initialCapacity, int capacityIncrement) 此构造函数用于创建一个具有指定初始容量和容量增量的空向量。 |
类方法
| 序号 | 方法和描述 |
|---|---|
| 1 | boolean add(E e) 此方法将指定的元素追加到此向量的末尾。 |
| 2 | void add(int index, E element) 此方法在此向量的指定位置插入指定的元素。 |
| 3 | boolean addAll(Collection<? extends E> c) 此方法将指定集合中的所有元素追加到此向量的末尾。 |
| 4 | boolean addAll(int index, Collection<? extends E> c) 此方法将指定集合中的所有元素插入到此向量的指定位置。 |
| 5 | void addElement(E obj) 此方法将指定的组件添加到此向量的末尾,将其大小增加一。 |
| 6 | int capacity() 此方法返回此向量的当前容量。 |
| 7 | void clear() 此方法从此向量中删除所有元素。 |
| 8 | clone clone() 此方法返回此向量的克隆。 |
| 9 | boolean contains(Object o) 如果此向量包含指定的元素,则此方法返回true。 |
| 10 | boolean containsAll(Collection<?> c) 如果此向量包含指定集合中的所有元素,则此方法返回true。 |
| 11 | void copyInto(Object[ ] anArray) 此方法将此向量的组件复制到指定的数组中。 |
| 12 | E elementAt(int index) 此方法返回指定索引处的组件。 |
| 13 | Enumeration<E> elements() 此方法返回此向量组件的枚举。 |
| 14 | void ensureCapacity(int minCapacity) 此方法根据需要增加此向量的容量,以确保它至少可以容纳最小容量参数指定的组件数量。 |
| 15 | boolean equals(Object o) 此方法将指定的Object与此Vector进行相等性比较。 |
| 16 | E firstElement() 此方法返回此向量的第一个组件(索引为0的项)。 |
| 17 | E get(int index) 此方法返回此向量中指定位置的元素。 |
| 18 | int hashCode() 此方法返回此向量的哈希码值。 |
| 19 | int indexOf(Object o) 此方法返回此向量中指定元素的第一次出现的索引,如果此向量不包含该元素,则返回-1。 |
| 20 | int indexOf(Object o, int index) 此方法返回此向量中指定元素的第一次出现的索引,从index向前搜索,如果找不到该元素,则返回-1。 |
| 21 | void insertElementAt(E obj, int index) 此方法将指定的对象作为组件插入到此向量的指定索引处。 |
| 22 | boolean isEmpty() 此方法测试此向量是否没有组件。 |
| 23 | E lastElement() 此方法返回向量的最后一个组件。 |
| 24 | int lastIndexOf(Object o) 此方法返回此向量中指定元素的最后一次出现的索引,如果此向量不包含该元素,则返回-1。 |
| 25 | int lastIndexOf(Object o, int index) 此方法返回此向量中指定元素的最后一次出现的索引,从index向后搜索,如果找不到该元素,则返回-1。 |
| 26 | E remove(int index) 此方法从此向量的指定位置删除元素。 |
| 27 | boolean remove(Object o) 此方法从此向量中删除指定元素的第一次出现。如果向量不包含该元素,则它保持不变。 |
| 28 | boolean removeAll(Collection<?> c) 此方法从此向量中删除所有包含在指定集合中的元素。 |
| 29 | void removeAllElements() 此方法从此向量中删除所有组件并将大小设置为零。 |
| 30 | boolean removeElement(Object obj) 此方法从此向量中删除参数的第一次出现。 |
| 31 | void removeElementAt(int index) 此方法删除指定索引处的组件。 |
| 32 | protected void removeRange(int fromIndex, int toIndex) 此方法从此列表中删除所有索引介于fromIndex(包含)和toIndex(不包含)之间的元素。 |
| 33 | boolean retainAll(Collection<?> c) 此方法仅保留此向量中包含在指定集合中的元素。 |
| 34 | E set(int index, E element) 此方法将此向量中指定位置的元素替换为指定的元素。 |
| 35 | void setElementAt(E obj, int index) 此方法将此向量的指定索引处的组件设置为指定的对象。 |
| 36 | void setSize(int newSize) 此方法设置此向量的尺寸。 |
| 37 | int size() 此方法返回此向量中组件的数量。 |
| 38 | List <E> subList(int fromIndex, int toIndex) 此方法返回此列表中从 fromIndex(包含)到 toIndex(不包含)的部分的视图。 |
| 39 | object[ ] toArray() 此方法返回一个数组,其中包含此向量中所有元素的正确顺序。 |
| 40 | <T> T[ ] toArray(T[ ] a) 此方法返回一个数组,其中包含此向量中所有元素的正确顺序;返回数组的运行时类型与指定数组的类型相同。 |
| 41 | String toString() 此方法返回此向量的字符串表示形式,其中包含每个元素的字符串表示形式。 |
| 42 | void trimToSize() 此方法将此向量的容量调整为向量的当前大小。 |
Java 数据结构 - 创建向量
java.util 类中的 Vector 类实现动态数组。它类似于 ArrayList,但有两个区别:Vector 是同步的,并且它包含许多不属于集合框架的遗留方法。
可以通过实例化 **java.util** 包中的 **Vector** 类来创建一个向量。
Vector vect = new Vector();
示例
import java.util.Vector;
public class CreatingVector {
public static void main(String args[]) {
Vector vect = new Vector();
vect.addElement("Java");
vect.addElement("JavaFX");
vect.addElement("HBase");
vect.addElement("Neo4j");
vect.addElement("Apache Flume");
System.out.println(vect);
}
}
输出
[Java, JavaFX, HBase, Neo4j, Apache Flume]
向 Vector 添加元素
**Vector** 类提供 **addElement()** 方法,它接受一个对象并将指定的对象/元素添加到当前向量中。
可以使用 **addElement()** 方法将元素添加到 Vector 对象中,方法是将要添加的元素/对象作为参数传递给此方法。
vect.addElement("Java");
示例
import java.util.Vector;
public class CreatingVector {
public static void main(String args[]) {
Vector vect = new Vector();
vect.addElement("Java");
vect.addElement("JavaFX");
vect.addElement("HBase");
vect.addElement("Neo4j");
vect.addElement("Apache Flume");
System.out.println(vect);
}
}
输出
[Java, JavaFX, HBase, Neo4j, Apache Flume]
从 Vector 中删除元素
**Vector** 类提供 **removeElement()** 方法,它接受一个对象并将指定的对象/元素从当前向量中移除。
可以使用 removeElement() 方法移除 Vector 对象的元素,方法是将要移除的元素的索引作为参数传递给此方法。
示例
import java.util.Vector;
public class RemovingElements {
public static void main(String args[]) {
Vector vect = new Vector();
vect.addElement("Java");
vect.addElement("JavaFX");
vect.addElement("HBase");
vect.addElement("Neo4j");
vect.addElement("Apache Flume");
System.out.println("Contents of the vector :"+vect);
vect.removeElement(3);
System.out.println("Contents of the vector after removing elements:"+vect);
}
}
输出
Contents of the vector :[Java, JavaFX, HBase, Neo4j, Apache Flume] Contents of the vector after removing elements:[Java, JavaFX, HBase, Neo4j, Apache Flume]
验证 Vector 是否为空
**java.util** 包中的 **Vector** 类提供 **isEmpty()** 方法。此方法验证当前向量是否为空。如果给定向量为空,则此方法返回 true,否则返回 false。
示例
import java.util.Vector;
public class Vector_IsEmpty {
public static void main(String args[]) {
Vector vect = new Vector();
vect.addElement("Java");
vect.addElement("JavaFX");
vect.addElement("HBase");
vect.addElement("Neo4j");
vect.addElement("Apache Flume");
System.out.println("Elements of the vector :"+vect);
boolean bool1 = vect.isEmpty();
if(bool1==true) {
System.out.println("Given vector is empty");
} else {
System.out.println("Given vector is not empty");
}
vect.clear();
boolean bool2 = vect.isEmpty();
System.out.println("cleared the contents of the vector");
if(bool2==true) {
System.out.println("Given vector is empty");
} else {
System.out.println("Given vector is not empty");
}
}
}
输出
Elements of the vector :[Java, JavaFX, HBase, Neo4j, Apache Flume] Given vector is not empty cleared the contents of the vector Given vector is empty
清除 Vector 的元素
可以使用 **clear()** 方法移除给定向量中的所有元素。
示例
import java.util.Vector;
public class ClearingElements {
public static void main(String args[]) {
Vector vect = new Vector();
vect.addElement("Java");
vect.addElement("JavaFX");
vect.addElement("HBase");
vect.addElement("Neo4j");
vect.addElement("Apache Flume");
System.out.println("Elements of the vector :"+vect);
vect.clear();
System.out.println("Elements of the vector after clearing it :"+vect);
}
}
输出
Elements of the vector :[Java, JavaFX, HBase, Neo4j, Apache Flume] Elements of the vector after clearing it :[]
打印 Vector 的元素
可以直接使用 println 语句打印向量的所有元素。
System.out.println(vect);
或者,可以使用 hasMoreElements() 和 nextElement() 方法逐个打印其元素。
示例
import java.util.*;
public class VectorPrintingElements {
public static void main(String args[]) {
// initial size is 3, increment is 2
Vector v = new Vector();
v.addElement(new Integer(1));
v.addElement(new Integer(2));
v.addElement(new Integer(3));
v.addElement(new Integer(4));
System.out.println("Capacity after four additions: " + v.capacity());
// enumerate the elements in the vector.
Enumeration vEnum = v.elements();
System.out.println("\nElements in vector:");
while(vEnum.hasMoreElements())
System.out.print(vEnum.nextElement() + " ");
System.out.println();
}
}
输出
Capacity after four additions: 10 Elements in vector: 1 2 3 4
Java 数据结构 - Stack 类
栈是一种抽象数据类型 (ADT),在大多数编程语言中常用。它被称为栈,因为它表现得像一个现实世界的栈,例如——一副牌或一堆盘子等。

现实世界的栈只允许在一端进行操作。例如,我们只能在栈的顶部放置或移除卡片或盘子。同样,Stack ADT 只允许在一端进行所有数据操作。在任何给定时间,我们只能访问栈的顶部元素。
此特性使其成为 LIFO 数据结构。LIFO 代表后进先出。在这里,最后放置(插入或添加)的元素首先被访问。在栈术语中,插入操作称为 **PUSH** 操作,移除操作称为 **POP** 操作。
栈表示
下图描述了一个栈及其操作:
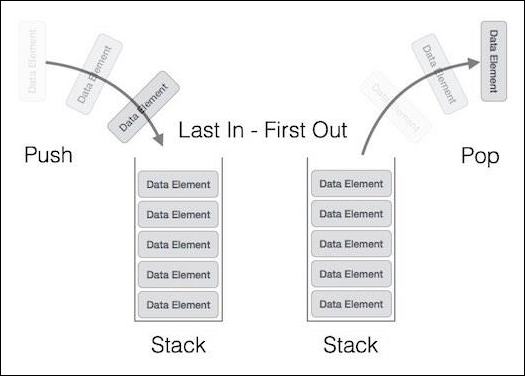
栈可以使用数组、结构、指针和链表实现。栈可以是固定大小的,也可以具有动态调整大小的功能。在这里,我们将使用数组实现栈,这使其成为固定大小的栈实现。
Stack 类
Stack 是 Vector 的一个子类,它实现标准的后进先出栈。
Stack 只定义默认构造函数,它创建一个空栈。Stack 包括 Vector 定义的所有方法,并添加了一些它自己的方法。
Stack( )
除了从其父类 Vector 继承的方法外,Stack 还定义了以下方法:
| 序号 | 方法和描述 |
|---|---|
| 1 | boolean empty() 测试此栈是否为空。如果栈为空,则返回 true;如果栈包含元素,则返回 false。 |
| 2 | Object peek( ) 返回栈顶的元素,但不将其移除。 |
| 3 | Object pop( ) 返回栈顶的元素,在此过程中将其移除。 |
| 4 | Object push(Object element) 将元素推入栈中。元素也会被返回。 |
| 5 | int search(Object element) 在栈中搜索元素。如果找到,则返回其距栈顶的偏移量。否则,返回 -1。 |
示例
下面的程序说明了此集合支持的几种方法:
import java.util.*;
public class StackDemo {
static void showpush(Stack st, int a) {
st.push(new Integer(a));
System.out.println("push(" + a + ")");
System.out.println("stack: " + st);
}
static void showpop(Stack st) {
System.out.print("pop -> ");
Integer a = (Integer) st.pop();
System.out.println(a);
System.out.println("stack: " + st);
}
public static void main(String args[]) {
Stack st = new Stack();
System.out.println("stack: " + st);
showpush(st, 42);
showpush(st, 66);
showpush(st, 99);
showpop(st);
showpop(st);
showpop(st);
try {
showpop(st);
} catch (EmptyStackException e) {
System.out.println("empty stack");
}
}
}
输出
stack: [ ] push(42) stack: [42] push(66) stack: [42, 66] push(99) stack: [42, 66, 99] pop -> 99 stack: [42, 66] pop -> 66 stack: [42] pop -> 42 stack: [ ] pop -> empty stack
Java 数据结构 - 创建栈
栈由 **java.util** 包中的 **Stack** 类表示。可以通过实例化此类来创建一个栈。
Stack stack = new Stack();
创建栈后,可以使用 addElement() 方法向其中添加元素。
stack.addElement("Java");
示例
以下是一个示例,演示如何创建栈,向其中添加元素以及显示其内容。
import java.util.Stack;
public class CreatingStack {
public static void main(String args[]) {
Stack stack = new Stack();
stack.addElement("Java");
stack.addElement("JavaFX");
stack.addElement("HBase");
stack.addElement("Flume");
stack.addElement("Java");
System.out.println(stack);
}
}
输出
Contents of the stack :[Java, JavaFX, HBase, Flume, Java]
向 Stack 推入元素
栈中的 push 操作涉及向其中插入元素。如果将特定元素推入栈,它将添加到栈的顶部,即第一个插入栈的元素是最后一个被弹出的元素。(先进后出)
可以使用 **push()** 方法将元素推入 Java 栈。
示例
import java.util.Stack;
public class PushingElements {
public static void main(String args[]) {
Stack stack = new Stack();
stack.push(455);
stack.push(555);
stack.push(655);
stack.push(755);
stack.push(855);
stack.push(955);
System.out.println(stack);
}
}
输出
[455, 555, 655, 755, 855, 955]
从 Stack 弹出元素
栈中的 pop 操作是指从栈中移除元素。对栈执行此操作时,将移除栈顶的元素,即最后插入栈的元素将首先弹出。(后进先出)
示例
import java.util.Stack;
public class PoppingElements {
public static void main(String args[]) {
Stack stack = new Stack();
stack.push(455);
stack.push(555);
stack.push(655);
stack.push(755);
stack.push(855);
stack.push(955);
System.out.println("Elements of the stack are :"+stack.pop());
System.out.println("Contents of the stack after popping the element :"+stack);
}
}
输出
Elements of the stack are :955 Contents of the stack after popping the element :[455, 555, 655, 755, 855]
验证 Stack 是否为空
**java.util** 包中的 Stack 类提供了一个 isEmpty() 方法。此方法验证当前 Stack 是否为空。如果给定向量为空,则此方法返回 true,否则返回 false。
示例
import java.util.Stack;
public class StackIsEmpty {
public static void main(String args[]) {
Stack stack = new Stack();
stack.push(455);
stack.push(555);
stack.push(655);
stack.push(755);
stack.push(855);
stack.push(955);
System.out.println("Contents of the stack :"+stack);
stack.clear();
System.out.println("Contents of the stack after clearing the elements :"+stack);
if(stack.isEmpty()) {
System.out.println("Given stack is empty");
} else {
System.out.println("Given stack is not empty");
}
}
}
输出
Contents of the stack :[455, 555, 655, 755, 855, 955] Contents of the stack after clearing the elements :[] Given stack is empty
清除 Stack 的元素
Stack 类的 **clear()** 方法用于清除当前栈的内容。
示例
import java.util.Stack;
public class ClearingElements {
public static void main(String[] args) {
Stack stack = new Stack();
stack.push(455);
stack.push(555);
stack.push(655);
stack.push(755);
stack.push(855);
stack.push(955);
System.out.println("Contents of the stack :"+stack);
stack.clear();
System.out.println("Contents of the stack after clearing the elements :"+stack);
}
}
输出
Contents of the stack :[455, 555, 655, 755, 855, 955] Contents of the stack after clearing the elements :[]
打印 Stack 的元素
可以直接使用 println() 方法打印栈的内容。
System.out.println(stack)
Stack 类还提供 iterator() 方法。此方法返回当前 Stack 的迭代器。使用它可以逐个打印栈的内容。
示例
import java.util.Iterator;
import java.util.Stack;
public class PrintingElements {
public static void main(String args[]) {
Stack stack = new Stack();
stack.push(455);
stack.push(555);
stack.push(655);
stack.push(755);
stack.push(855);
stack.push(955);
System.out.println("Contents of the stack :");
Iterator it = stack.iterator();
while(it.hasNext()) {
System.out.println(it.next());
}
}
}
输出
Contents of the stack : 455 555 655 755 855 955
Java 数据结构 - 优先队列类
队列是一种抽象数据结构,与栈有点类似。与栈不同,队列的两端都是开放的。一端始终用于插入数据(入队),另一端用于移除数据(出队)。队列遵循先进先出方法,即首先存储的数据项将首先被访问。
队列表示
正如我们现在了解的那样,在队列中,我们出于不同的原因访问两端。下图试图解释队列作为数据结构的表示:

与栈一样,队列也可以使用数组、链表、指针和结构实现。为简单起见,我们将使用一维数组实现队列。
优先队列类
**java.util.PriorityQueue** 类是一个基于优先级堆的无界优先级队列。以下是关于 PriorityQueue 的重要几点:
优先级队列的元素根据它们的自然顺序或在队列构造时提供的比较器进行排序,具体取决于使用哪个构造函数。
优先级队列不允许空元素。
依赖自然顺序的优先级队列也不允许插入不可比较的对象。
类声明
以下是 **java.util.PriorityQueue** 类的声明:
public class PriorityQueue<E> extends AbstractQueue<E> implements Serializable
参数
以下是 **java.util.PriorityQueue** 类的参数:
**E** - 这是此集合中保存的元素的类型。
类构造函数
| 序号 | 构造函数和描述 |
|---|---|
| 1 | PriorityQueue() 这将创建一个具有默认初始容量 (11) 的 PriorityQueue,该队列根据其自然顺序对元素进行排序。 |
| 2 | PriorityQueue(Collection<? extends E> c) 这将创建一个包含指定集合中元素的 PriorityQueue。 |
| 3 | PriorityQueue(int initialCapacity) 这将创建一个具有指定初始容量的 PriorityQueue,该队列根据其自然顺序对元素进行排序。 |
| 4 | PriorityQueue(int initialCapacity, Comparator<? super E> comparator) 这将创建一个具有指定初始容量的 PriorityQueue,该队列根据指定的比较器对元素进行排序。 |
| 5 | PriorityQueue(PriorityQueue<? extends E> c) 这将创建一个包含指定优先级队列中元素的 PriorityQueue。 |
| 6 | PriorityQueue(SortedSet<? extends E> c) 这将创建一个包含指定有序集合中元素的 PriorityQueue。 |
类方法
| 序号 | 方法和描述 |
|---|---|
| 1 | boolean add(E e) 此方法将指定的元素插入到此优先级队列中。 |
| 2 | void clear() 此方法将从此优先级队列中移除所有元素。 |
| 3 | Comparator<? super E> comparator() 此方法返回用于对此队列中的元素进行排序的比较器,如果此队列根据其元素的自然顺序进行排序,则返回 null。 |
| 4 | boolean contains(Object o) 此方法如果此队列包含指定的元素,则返回 true。 |
| 5 | Iterator<E> iterator() 此方法返回此队列中元素的迭代器。 |
| 6 | boolean offer(E e) 此方法将指定的元素插入到此优先级队列中。 |
| 7 | E peek() 此方法检索但不移除此队列的头部,如果此队列为空,则返回 null。 |
| 8 | E poll() 此方法检索并移除此队列的头部,如果此队列为空,则返回 null。 |
| 9 | boolean remove(Object o) 此方法从此队列中移除指定元素的一个实例(如果存在)。 |
| 10 | int size() 此方法返回此集合中的元素数量。 |
| 11 | Object[] toArray() 此方法返回一个包含此队列中所有元素的数组。 |
| 12 | <T> T[] toArray(T[] a) 此方法返回一个包含此队列中所有元素的数组;返回数组的运行时类型与指定数组的类型相同。 |
Java 数据结构 - 创建队列
Java 提供了一个名为 Queue 的接口,它表示队列数据结构。此接口具有各种子类,例如 ArrayBlockingQueue、ArrayDeque、ConcurrentLinkedDeque、ConcurrentLinkedQueue、DelayQueue、LinkedBlockingDeque、LinkedBlockingQueue、LinkedList、LinkedTransferQueue、PriorityBlockingQueue、PriorityQueue、SynchronousQueue。
可以通过实例化这些类中的任何一个来在 Java 中创建一个队列。在我们的示例中,我们将尝试通过实例化 **PriorityQueue** 类来创建一个队列。
它是一个基于优先级堆的无界优先级队列。
它的元素根据它们的自然顺序或在队列构造时提供的比较器进行排序,具体取决于使用哪个构造函数。
它不允许空元素。
它依赖自然顺序也不允许插入不可比较的对象。
示例
import java.util.PriorityQueue;
import java.util.Queue;
public class CreatingQueue {
public static void main(String args[]) {
//Create priority queue
Queue <String> prQueue = new PriorityQueue <String> () ;
//Adding elements
prQueue.add("JavaFX");
prQueue.add("Java");
prQueue.add("HBase");
prQueue.add("Flume");
prQueue.add("Neo4J");
System.out.println("Priority queue values are: " + prQueue) ;
}
}
输出
Priority queue values are: [Flume, HBase, Java, JavaFX, Neo4J]
向 Queue 添加元素
队列接口的 **add()** 方法接受一个元素作为参数,并将其添加到当前队列中。
要向队列添加元素,请实例化队列接口的任何子类,并使用 add() 方法添加元素。
示例
import java.util.PriorityQueue;
import java.util.Queue;
public class CreatingQueue {
public static void main(String args[]) {
//Create priority queue
Queue <String> prQueue = new PriorityQueue <String> ();
//Adding elements
prQueue.add("JavaFX");
prQueue.add("Java");
prQueue.add("HBase");
prQueue.add("Flume");
prQueue.add("Neo4J");
System.out.println("Priority queue values are: " + prQueue) ;
}
}
输出
Priority queue values are: [Flume, HBase, Java, JavaFX, Neo4J]
从 Queue 中删除元素
与 add() 方法类似,Queue 接口提供 remove() 方法。此方法接受一个元素作为参数,并将其从队列中移除。
使用此方法可以从队列中移除元素。
示例
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class RemovingElements {
public static void main(String args[]) {
//Create priority queue
Queue <String> prQueue = new PriorityQueue <String> () ;
//Adding elements
prQueue.add("JavaFX");
prQueue.add("Java");
prQueue.add("HBase");
prQueue.add("Flume");
prQueue.add("Neo4J");
System.out.println("Enter the element to be deleted");
Scanner sc = new Scanner(System.in);
String element = sc.next();
System.out.println("Contents of the queue : " + prQueue) ;
prQueue.remove(element);
System.out.println("Contents of the queue after deleting sepcified element: " + prQueue) ;
}
}
清除 Queue 的元素
Queue 接口提供了一个名为 **clear()** 的方法。此方法用于从当前队列中移除所有元素。
示例
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class ClearingElements {
public static void main(String args[]) {
//Create priority queue
Queue <String> prQueue = new PriorityQueue <String> () ;
//Adding elements
prQueue.add("JavaFX");
prQueue.add("Java");
prQueue.add("HBase");
prQueue.add("Flume");
prQueue.add("Neo4J");
System.out.println("Contents of the queue : " + prQueue) ;
prQueue.clear();
System.out.println("Contents of the queue after deleting specified element: " + prQueue) ;
}
}
输出
Contents of the queue : [Flume, HBase, Java, JavaFX, Neo4J] Contents of the queue after deleting specified element: []
打印 Queue 的元素
可以使用 println() 方法直接打印队列的内容。
System.out.println(queue)
除此之外,Queue 还提供 iterator() 方法,该方法返回当前队列的迭代器。使用它可以逐个打印其内容。
示例
import java.util.Iterator;
import java.util.PriorityQueue;
import java.util.Queue;
public class PrintingElements {
public static void main(String args[]) {
// Create priority queue
Queue <String> prQueue = new PriorityQueue <String> () ;
// Adding elements
prQueue.add("JavaFX");
prQueue.add("Java");
prQueue.add("HBase");
prQueue.add("Flume");
prQueue.add("Neo4J");
Iterator iT = prQueue.iterator();
System.out.println("Contents of the queue are :");
while(iT.hasNext()) {
System.out.println(iT.next());
}
}
}
输出
Contents of the queue are : Flume HBase Java JavaFX Neo4J
Java 数据结构 - 链表类
介绍
java.util.LinkedList类的操作实现了双向链表的预期功能。对列表进行索引的操作将从列表的开头或结尾开始遍历,选择离指定索引较近的一端。
类声明
以下是java.util.LinkedList类的声明:
public class LinkedList<E> extends AbstractSequentialList<E> implements List<E>, Deque<E>, Cloneable, Serializable
参数
以下是java.util.LinkedList类的参数:
**E** - 这是此集合中保存的元素的类型。
字段
继承自java.util.AbstractList类的字段。
类构造函数
| 序号 | 构造函数和说明 |
|---|---|
| 1 | LinkedList() 此构造函数创建一个空列表。 |
| 2 | LinkedList(Collection<? extends E> c) 此构造函数创建一个列表,其中包含指定集合的元素,顺序与集合迭代器返回的顺序相同。 |
类方法
| 序号 | 方法和说明 |
|---|---|
| 1 | boolean add(E e) 此方法将指定的元素添加到此列表的末尾。 |
| 2 | void add(int index, E element) 此方法在此列表的指定位置插入指定的元素。 |
| 3 | boolean addAll(Collection<? extends E> c) 此方法将指定集合中的所有元素添加到此列表的末尾,顺序与指定集合的迭代器返回的顺序相同。 |
| 4 | boolean addAll(int index, Collection<? extends E> c) 此方法将指定集合中的所有元素插入到此列表中,从指定位置开始。 |
| 5 | void addFirst(E e) 此方法将指定的元素插入到此列表的开头。 |
| 6 | void addLast(E e) 此方法将指定的元素添加到此列表的末尾。 |
| 7 | void clear() 此方法从此列表中移除所有元素。 |
| 8 | Object clone() 此方法返回此LinkedList的浅拷贝。 |
| 9 | boolean contains(Object o) 此方法如果此列表包含指定的元素,则返回true。 |
| 10 | Iterator<E> descendingIterator() 此方法返回一个迭代器,用于反向顺序遍历此双端队列中的元素。 |
示例
package com.tutorialspoint;
import java.util.*;
public class LinkedListDemo {
public static void main(String[] args) {
// create a LinkedList
LinkedList list = new LinkedList();
// add some elements
list.add("Hello");
list.add(2);
list.add("Chocolate");
list.add("10");
// print the list
System.out.println("LinkedList:" + list);
// add a new element at the end of the list
list.add("Element");
// print the updated list
System.out.println("LinkedList:" + list);
}
}
输出
LinkedList:[Hello, 2, Chocolate, 10] LinkedList:[Hello, 2, Chocolate, 10, Element]
链表是由一系列链接组成的序列,每个链接包含一个指向另一个链接的连接。链表是仅次于数组的第二常用数据结构。
链表表示
链表可以可视化为一个节点链,其中每个节点都指向下一个节点。
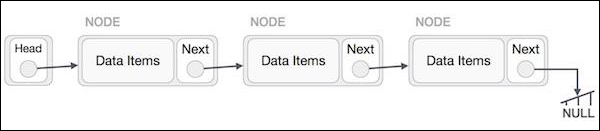
每个链表包含一个头节点和一个或多个节点。
每个节点存储数据以及下一个元素的地址。
列表的最后一个元素为null,标志着列表的结尾。
链表有三种类型
单链表 - 只能向前遍历项目。
双向链表 - 可以向前和向后遍历项目。
循环链表 - 最后一个项目包含指向第一个元素的下一个链接,而第一个元素包含指向最后一个元素的上一个链接。
Java数据结构 - 创建链表
java.util包中的LinkedList类表示Java中的单链表。可以通过实例化此类来创建一个链表。
LinkedList linkedLlist = new LinkedList();
示例
import java.util.LinkedList;
public class CreatingLinkedList {
public static void main(String args[]) {
LinkedList linkedList = new LinkedList();
linkedList.add("Mangoes");
linkedList.add("Grapes");
linkedList.add("Bananas");
linkedList.add("Oranges");
linkedList.add("Pineapples");
System.out.println("Contents of the linked list :"+linkedList);
}
}
输出
Contents of the linked list :[Mangoes, Grapes, Bananas, Oranges, Pineapples]
向链表添加元素
LinkedList类提供了一个名为add()的方法。此方法接受一个元素作为参数,并将其添加到列表的末尾。
可以使用此方法向链表添加元素。
示例
import java.util.LinkedList;
public class CreatingLinkedList {
public static void main(String args[]) {
LinkedList linkedList = new LinkedList();
linkedList.add("Mangoes");
linkedList.add("Grapes");
linkedList.add("Bananas");
linkedList.add("Oranges");
linkedList.add("Pineapples");
System.out.println("Contents of the linked list :"+linkedList);
}
}
输出
Contents of the linked list :[Mangoes, Grapes, Bananas, Oranges, Pineapples]
从链表中删除元素
LinkedList类的remove()方法接受一个元素作为参数,并将其从当前链表中移除。
可以使用此方法从链表中移除元素。
示例
import java.util.LinkedList;
public class RemovingElements {
public static void main(String[] args) {
LinkedList linkedList = new LinkedList();
linkedList.add("Mangoes");
linkedList.add("Grapes");
linkedList.add("Bananas");
linkedList.add("Oranges");
linkedList.add("Pineapples");
System.out.println("Contents of the linked list :"+linkedList);
linkedList.remove("Grapes");
System.out.println("Contents of the linked list after removing the specified element :"+linkedList);
}
}
输出
Contents of the linked list :[Mangoes, Grapes, Bananas, Oranges, Pineapples] Contents of the linked list after removing the specified element :[Mangoes, Bananas, Oranges, Pineapples]
Java数据结构 - 双向链表
双向链表是链表的一种变体,与单链表相比,可以轻松地向前和向后两种方式遍历。以下是理解双向链表概念的一些重要术语。
链接 - 链表的每个链接都可以存储称为元素的数据。
Next - 链表的每个链接都包含指向下一个链接的链接,称为Next。
Prev - 链表的每个链接都包含指向前一个链接的链接,称为Prev。
LinkedList - 链表包含指向第一个链接(称为First)和最后一个链接(称为Last)的连接链接。
双向链表表示
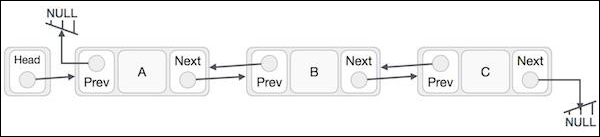
- 双向链表包含一个名为first和last的链接元素。
- 每个链接都包含一个或多个数据字段和两个链接字段,分别称为next和prev。
- 每个链接都使用其next链接与其下一个链接链接。
- 每个链接都使用其prev链接与其前一个链接链接。
- 最后一个链接的链接为null,标志着列表的结尾。
示例
class Node{
int data;
Node preNode, nextNode, CurrentNode;
Node() {
preNode = null;
nextNode = null;
}
Node(int data) {
this.data = data;
}
}
public class DoublyLinked {
Node head, tail;
int size;
public void printData() {
System.out.println(" ");
Node node = head;
while(node !=null) {
System.out.println(node.data);
node = node.nextNode;
}
System.out.println( );
}
public void insertStart(int data) {
Node node = new Node();
node.data = data;
node.nextNode = head;
node.preNode = null;
if(head!=null) {
head.preNode = node;
}
head = node;
if(tail == null) {
tail = node;
}
size++;
}
public void insertEnd(int data) {
Node node = new Node();
node.data = data;
node.nextNode = null;
node.preNode = tail;
if(tail!=null) {
tail.preNode = node;
}
tail = node;
if(head == null) {
head = node;
}
size++;
}
public static void main(String args[]) {
DoublyLinked dl = new DoublyLinked();
dl.insertStart(10);
dl.insertStart(20);
dl.insertStart(30);
dl.insertStart(1);
dl.insertStart(56);
dl.insertStart(40);
dl.printData();
}
}
输出
40 56 1 30 20 10
Java数据结构 - 循环链表
循环链表是链表的一种变体,其中第一个元素指向最后一个元素,最后一个元素指向第一个元素。单链表和双向链表都可以转换为循环链表。
单链表作为循环链表
在单链表中,最后一个节点的next指针指向第一个节点。

双向链表作为循环链表
在双向链表中,最后一个节点的next指针指向第一个节点,第一个节点的prev指针指向最后一个节点,从而形成双向循环链表。

根据以上说明,需要注意以下几点:
在单链表和双向链表中,最后一个链接的next都指向列表的第一个链接。
在双向链表中,第一个链接的previous指向列表的最后一个链接。
示例
class Node{
int data;
Node preNode, nextNode, CurrentNode;
Node() {
preNode = null;
nextNode = null;
}
Node(int data) {
this.data = data;
}
}
public class CircularLinked {
Node head, tail;
int size;
public void printData() {
Node node = head;
if(size<=0) {
System.out.print("List is empty");
} else {
do {
System.out.print(" " + node.data);
node = node.nextNode;
}
while(node!=head);
}
}
public void insertStart(int data) {
Node node = new Node();
node.data = data;
node.nextNode = head;
node.preNode = null;
if(size==0) {
head = node;
tail = node;
node.nextNode = head;
} else {
Node tempNode = head;
node.nextNode = tempNode;
head = node;
tail.nextNode = node;
}
size++;
}
public void insertEnd(int data) {
if(size==0) {
insertStart(data);
} else {
Node node = new Node();
tail.nextNode =node;
tail = node;
tail.nextNode = head;
size++;
}
}
public static void main(String args[]) {
CircularLinked dl = new CircularLinked();
dl.insertStart(10);
dl.insertStart(20);
dl.insertStart(30);
dl.insertStart(1);
dl.insertStart(56);
dl.insertStart(40);
dl.printData();
}
}
输出
40 56 1 30 20 10
Java数据结构 - Set接口
Set是一个无序的集合,不允许重复元素。它模拟了数学集合的抽象概念。当我们向其中添加元素时,它会动态增长。Set类似于数组。
Set接口
Set是一个不能包含重复元素的集合。它模拟了数学集合的抽象概念。
Set接口仅包含从Collection继承的方法,并增加了禁止重复元素的限制。
Set还在equals和hashCode操作的行为上增加了更严格的约定,允许即使Set实例的实现类型不同,也可以有意义地进行比较。
Set声明的方法总结在下表中:
| 序号 | 方法和描述 |
|---|---|
| 1 | add( ) 向集合中添加一个对象。 |
| 2 | clear( ) 从集合中移除所有对象。 |
| 3 | contains( ) 如果指定的对象是集合中的元素,则返回true。 |
| 4 | isEmpty( ) 如果集合没有元素,则返回true。 |
| 5 | iterator( ) 返回集合的Iterator对象,可用于检索对象。 |
| 6 | remove( ) 从集合中移除指定的元素。 |
| 7 | size( ) 返回集合中元素的数量。 |
示例
Set在HashSet、TreeSet、LinkedHashSet等多个类中都有实现。以下是一个解释Set功能的示例:
import java.util.*;
public class SetDemo {
public static void main(String args[]) {
int count[] = {34, 22,10,60,30,22};
Set<Integer> set = new HashSet<Integer>();
try {
for(int i = 0; i < 5; i++) {
set.add(count[i]);
}
System.out.println(set);
TreeSet sortedSet = new TreeSet<Integer>(set);
System.out.println("The sorted list is:");
System.out.println(sortedSet);
System.out.println("The First element of the set is: "+ (Integer)sortedSet.first());
System.out.println("The last element of the set is: "+ (Integer)sortedSet.last());
}
catch(Exception e) {}
}
}
输出
[34, 22, 10, 60, 30] The sorted list is: [10, 22, 30, 34, 60] The First element of the set is: 10 The last element of the set is: 60
Java数据结构 - 创建Set
java.util包中的Set接口表示Java中的集合。HashSet和LinkedHashSet类实现了此接口。
要创建一个集合(对象),需要实例化这两个类中的一个。
Set set = new HashSet();
示例
import java.util.HashSet;
import java.util.Set;
public class CreatingSet {
public static void main(String args[]) {
Set set = new HashSet();
set.add(100);
set.add(501);
set.add(302);
set.add(420);
System.out.println("Contents of the set are: "+set);
}
}
输出
Contents of the set are: [100, 420, 501, 302]
向 Set 添加元素
可以使用Set接口的add()方法向集合中添加元素。此方法接受一个元素作为参数,并将给定的元素/对象添加到集合中。
示例
import java.util.HashSet;
import java.util.Set;
public class CreatingSet {
public static void main(String args[]) {
Set set = new HashSet();
set.add(100);
set.add(501);
set.add(302);
set.add(420);
System.out.println("Contents of the set are: "+set);
}
}
输出
Contents of the set are: [100, 420, 501, 302]
从 Set 中删除元素
Set接口的remove()方法接受一个元素作为参数,并将其从当前集合中删除。
可以使用此方法从集合中移除元素。
示例
import java.util.HashSet;
import java.util.Set;
public class RemovingElements {
public static void main(String args[]) {
Set set = new HashSet();
set.add(100);
set.add(501);
set.add(302);
set.add(420);
System.out.println("Contents of the set are: "+set);
set.remove(100);
System.out.println("Contents of the set after removing one element : "+set);
}
}
输出
Contents of the set are: [100, 420, 501, 302] Contents of the set after removing one element : [420, 501, 302]
Java数据结构 - 遍历Set
Set接口继承了Iterator接口,因此它提供了iterator()方法。此方法返回当前集合的迭代器对象。
迭代器对象允许调用两个方法:
hasNext() - 此方法验证当前对象是否包含更多元素,如果包含则返回true。
next() - 此方法返回当前对象的下一个元素。
使用这两个方法,可以在Java中遍历Set。
示例
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
public class LoopThroughSet {
public static void main(String args[]) {
Set set = new HashSet();
set.add(100);
set.add(501);
set.add(302);
set.add(420);
System.out.println("Contents of the set are: ");
Iterator iT = set.iterator();
while( iT.hasNext()) {
System.out.println(iT.next());
}
}
}
输出
Contents of the set are: 100 420 501 302
Java数据结构 - 合并两个Set
Set接口提供了一个名为addAll()的方法(从Collection接口继承),可以使用此方法将一个集合的内容添加到另一个集合中。
示例
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
public class AddingTwoSets {
public static void main(String args[]) {
Set set1 = new HashSet();
set1.add(100);
set1.add(501);
set1.add(302);
set1.add(420);
System.out.println("Contents of set1 are: ");
System.out.println(set1);
Set set2 = new HashSet();
set2.add(200);
set2.add(630);
set2.add(987);
set2.add(665);
System.out.println("Contents of set2 are: ");
System.out.println(set2);
set1.addAll(set2);
System.out.println("Contents of set1 after addition: ");
System.out.println(set1);
}
}
输出
Contents of set1 are: [100, 420, 501, 302] Contents of set2 are: [630, 200, 665, 987] Contents of set1 after addition: [100, 420, 501, 630, 200, 665, 987, 302]
Java数据结构 - 两个Set的差集
假设我们通过添加两个(或更多)集合的内容来创建一个集合对象,当需要从该集合中完全移除特定集合的内容时,可以使用removeAll()方法。
此方法属于Set接口,它继承自Collection接口。它接受一个集合对象,并一次性将它的内容从当前Set(对象)中完全移除。
示例
import java.util.HashSet;
import java.util.Set;
public class SubtractingTwoSets {
public static void main(String args[]) {
Set set1 = new HashSet();
set1.add(100);
set1.add(501);
set1.add(302);
set1.add(420);
System.out.println("Contents of set1 are: ");
System.out.println(set1);
Set set2 = new HashSet();
set2.add(200);
set2.add(630);
set2.add(987);
set2.add(665);
System.out.println("Contents of set2 are: ");
System.out.println(set2);
set1.addAll(set2);
System.out.println("Contents of set1 after addition: ");
System.out.println(set1);
set1.removeAll(set2);
System.out.println("Contents of set1 after removal");
System.out.println(set1);
}
}
输出
Contents of set1 are: [100, 420, 501, 302] Contents of set2 are: [630, 200, 665, 987] Contents of set1 after addition: [100, 420, 501, 630, 200, 665, 987, 302] Contents of set1 after removal [100, 420, 501, 302]
Java数据结构 - Dictionary类
Dictionary类是一个抽象类,它表示存储键值对的数据结构。其中的每个键都与一个值相关联,可以使用其各自的键检索这些值。
因此,像映射一样,字典也可以理解(认为)为键值对的列表。
Java中的Dictionary类
Dictionary是一个抽象类,表示键值存储库,其操作方式与Map非常相似。
给定键和值,可以在Dictionary对象中存储该值。存储值后,可以使用其键检索它。因此,像映射一样,字典可以被认为是键值对的列表。
Dictionary定义的抽象方法如下:
| 序号 | 方法和描述 |
|---|---|
| 1 | Enumeration elements( ) 返回字典中包含的值的枚举。 |
| 2 | Object get(Object key) 返回包含与键关联的值的对象。如果键不在字典中,则返回null对象。 |
| 3 | boolean isEmpty( ) 如果字典为空,则返回true;如果字典至少包含一个键,则返回false。 |
| 4 | Enumeration keys( ) 返回字典中包含的键的枚举。 |
| 5 | Object put(Object key, Object value) 将键及其值插入字典。如果键不在字典中,则返回null;如果键已在字典中,则返回与键关联的先前值。 |
| 6 | Object remove(Object key) 移除键及其值。返回与键关联的值。如果键不在字典中,则返回null。 |
| 7 | int size( ) 返回字典中条目的数量。 |
Dictionary 类已过时。应实现 Map 接口以获得键值存储功能。
示例
package com.tutorialspoint;
import java.util.*;
public class DictionaryDemo {
public static void main(String[] args) {
// create a new hasthtable
Dictionary d = new Hashtable();
// put some elements
d.put("1", "Chocolate");
d.put("2", "Cocoa");
d.put("5", "Coffee");
// print how many times put was called
System.out.println("Number of times put was called:" + d.size());
}
}
输出
Number of times put was called:3
Java 数据结构 - 创建字典
由于 Dictionary 是一个抽象类,因此不能直接实例化它。HashTable 类是 Dictionary 类的子类。因此,您可以通过实例化此类来创建字典对象。
Dictionary dic = new Hashtable();
示例
import java.util.Hashtable;
import java.util.Dictionary;
public class CreatingDictionary {
public static void main(String args[]) {
Dictionary dic = new Hashtable();
dic.put("Ram", 94.6);
dic.put("Rahim", 92);
dic.put("Robert", 85);
dic.put("Roja", 93);
dic.put("Raja", 75);
System.out.println(dic);
}
}
输出
{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
向字典添加元素
Dictionary 类提供了一个名为 put() 的方法,此方法接受键值对(对象)作为参数并将其添加到字典中。
您可以使用此方法向字典中添加元素。
示例
import java.util.Hashtable;
import java.util.Dictionary;
public class CreatingDictionary {
public static void main(String args[]) {
Dictionary dic = new Hashtable();
dic.put("Ram", 94.6);
dic.put("Rahim", 92);
dic.put("Robert", 85);
dic.put("Roja", 93);
dic.put("Raja", 75);
System.out.println(dic);
}
}
输出
{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
从字典中删除元素
您可以使用字典类的 remove() 方法删除字典中的元素。此方法接受键或键值对并删除相应的元素。
dic.remove("Ram");
or
dic.remove("Ram", 94.6);
示例
import java.util.Hashtable;
import java.util.Dictionary;
public class RemovingElements {
public static void main(String args[]) {
Dictionary dic = new Hashtable();
dic.put("Ram", 94.6);
dic.put("Rahim", 92);
dic.put("Robert", 85);
dic.put("Roja", 93);
dic.put("Raja", 75);
System.out.println("Contents of the hash table :"+dic);
dic.remove("Ram");
System.out.println("Contents of the hash table after deleting specified elements :"+dic);
}
}
输出
Contents of the hash table :{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
Contents of the hash table after deleting specified elements :{Rahim = 92, Roja = 93, Raja = 75, Robert = 85}
检索字典中的值
您可以使用 Dictionary 类的 get() 方法检索特定键的值。如果将特定元素的键作为此方法的参数传递,则它将返回指定键的值(作为对象)。如果字典在指定的键下不包含任何元素,则返回 null。
您可以使用此方法检索字典中的值。
示例
import java.util.Hashtable;
import java.util.Dictionary;
public class RetrievingElements {
public static void main(String args[]) {
Dictionary dic = new Hashtable();
dic.put("Ram", 94.6);
dic.put("Rahim", 92);
dic.put("Robert", 85);
dic.put("Roja", 93);
dic.put("Raja", 75);
Object ob = dic.get("Ram");
System.out.println("Value of the specified key :"+ ob);
}
}
输出
Value of the specified key :94.6
遍历字典
Dictionary 类提供了一个名为 keys() 的方法,该方法返回一个枚举对象,其中包含哈希表中的所有键。
使用此方法获取键,并使用 get() 方法检索每个键的值。
Enumeration(接口)的 hasMoreElements() 方法如果枚举对象还有更多元素则返回 true。您可以使用此方法运行循环。
示例
import java.util.Enumeration;
import java.util.Hashtable;
import java.util.Dictionary;
public class Loopthrough {
public static void main(String args[]) {
String str;
Dictionary dic = new Hashtable();
dic.put("Ram", 94.6);
dic.put("Rahim", 92);
dic.put("Robert", 85);
dic.put("Roja", 93);
dic.put("Raja", 75);
Enumeration keys = dic.keys();
System.out.println("Contents of the hash table are :");
while(keys.hasMoreElements()) {
str = (String) keys.nextElement();
System.out.println(str + ": " + dic.get(str));
}
}
}
输出
Contents of the hash table are : Rahim: 92 Roja: 93 Raja: 75 Ram: 94.6 Robert: 85
Java 数据结构 - HashTable 类
哈希表是一种以关联方式存储数据的数据结构。在哈希表中,数据以数组格式存储,其中每个数据值都有其自己的唯一索引值。如果我们知道所需数据的索引,则数据访问速度非常快。
因此,它成为一个数据结构,其中插入和搜索操作非常快,而不管数据的大小如何。哈希表使用数组作为存储介质,并使用哈希技术生成要插入元素或从中定位元素的索引。
Java 的 HashTable 类
Hashtable 是最初的 java.util 的一部分,它是 Dictionary 的具体实现。
但是,Java 2 重新设计了 Hashtable,使其也实现了 Map 接口。因此,Hashtable 现在已集成到集合框架中。它类似于 HashMap,但它是同步的。
与 HashMap 一样,Hashtable 在哈希表中存储键值对。使用 Hashtable 时,您指定用作键的对象以及要链接到该键的值。然后对键进行哈希处理,生成的哈希代码用作在表中存储值的索引。
以下是 HashTable 类提供的构造函数列表。
| 序号 | 构造函数和描述 |
|---|---|
| 1 | Hashtable( ) 这是哈希表的默认构造函数,它实例化 HashTable 类。 |
| 2 | Hashtable(int size) 此构造函数接受一个整数参数,并创建一个哈希表,其初始大小由整数 value size 指定。 |
| 3 | Hashtable(int size, float fillRatio) 这将创建一个哈希表,其初始大小由 size 指定,填充率由 fillRatio 指定。此比率必须在 0.0 和 1.0 之间,它决定了哈希表在向上调整大小之前可以填充的程度。 |
| 4 | Hashtable(Map < ? extends K, ? extends V > t) 这将使用给定的映射构造一个 Hashtable。 |
除了 Map 接口定义的方法外,Hashtable 还定义了以下方法
| 序号 | 方法和描述 |
|---|---|
| 1 | void clear( ) 重置并清空哈希表。 |
| 2 | Object clone( ) 返回调用对象的副本。 |
| 3 | boolean contains(Object value) 如果哈希表中存在与 value 相等的值,则返回 true。如果找不到该值,则返回 false。 |
| 4 | boolean containsKey(Object key) 如果哈希表中存在与 key 相等的键,则返回 true。如果找不到该键,则返回 false。 |
| 5 | boolean containsValue(Object value) 如果哈希表中存在与 value 相等的值,则返回 true。如果找不到该值,则返回 false。 |
| 6 | Enumeration elements( ) 返回哈希表中包含的值的枚举。 |
| 7 | Object get(Object key) 返回包含与 key 关联的值的对象。如果 key 不在哈希表中,则返回 null 对象。 |
| 8 | boolean isEmpty( ) 如果哈希表为空,则返回 true;如果它至少包含一个键,则返回 false。 |
| 9 | Enumeration keys( ) 返回哈希表中包含的键的枚举。 |
| 10 | Object put(Object key, Object value) 将键和值插入哈希表。如果键不在哈希表中,则返回 null;如果键已在哈希表中,则返回与键关联的先前值。 |
| 11 | void rehash( ) 增加哈希表的大小并重新哈希其所有键。 |
| 12 | Object remove(Object key) 删除键及其值。返回与键关联的值。如果键不在哈希表中,则返回 null 对象。 |
| 13 | int size( ) 返回哈希表中的条目数。 |
| 14 | String toString( ) 返回哈希表的字符串等效项。 |
示例
以下程序演示了此数据结构支持的几种方法
import java.util.*;
public class HashTableDemo {
public static void main(String args[]) {
// Create a hash map
Hashtable balance = new Hashtable();
Enumeration names;
String str;
double bal;
balance.put("Zara", new Double(3434.34));
balance.put("Mahnaz", new Double(123.22));
balance.put("Ayan", new Double(1378.00));
balance.put("Daisy", new Double(99.22));
balance.put("Qadir", new Double(-19.08));
// Show all balances in hash table.
names = balance.keys();
while(names.hasMoreElements()) {
str = (String) names.nextElement();
System.out.println(str + ": " + balance.get(str));
}
System.out.println();
// Deposit 1,000 into Zara's account
bal = ((Double)balance.get("Zara")).doubleValue();
balance.put("Zara", new Double(bal + 1000));
System.out.println("Zara's new balance: " + balance.get("Zara"));
}
}
输出
Qadir: -19.08 Zara: 3434.34 Mahnaz: 123.22 Daisy: 99.22 Ayan: 1378.0 Zara's new balance: 4434.34
Java 数据结构 - 创建哈希表
Java 包 java.util 提供了一个名为 HashTable 的类,它表示哈希表。这存储键值对,使用 Hashtable 时,您指定用作键的对象以及要链接到该键的值。然后对键进行哈希处理,生成的哈希代码用作在表中存储值的索引。
您可以通过实例化 HashTable 类来创建哈希表。
HashTable hashTable = new HashTable();
示例
import java.util.Hashtable;
public class CreatingHashTable {
public static void main(String args[]) {
Hashtable hashTable = new Hashtable();
hashTable.put("Ram", 94.6);
hashTable.put("Rahim", 92);
hashTable.put("Robert", 85);
hashTable.put("Roja", 93);
hashTable.put("Raja", 75);
System.out.println(hashTable);
}
}
输出
{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
向哈希表添加元素
HashTable 类提供了一个名为 put() 的方法,此方法接受键值对(对象)作为参数并将其添加到当前哈希表中。
您可以使用此方法将键值对添加到当前哈希表中。
示例
import java.util.Hashtable;
public class CreatingHashTable {
public static void main(String args[]) {
Hashtable hashTable = new Hashtable();
hashTable.put("Ram", 94.6);
hashTable.put("Rahim", 92);
hashTable.put("Robert", 85);
hashTable.put("Roja", 93);
hashTable.put("Raja", 75);
System.out.println(hashTable);
}
}
输出
{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
从哈希表中删除元素
您可以删除哈希表中的元素,您可以使用 HashTable 类的 remove() 方法。
对于此方法,您需要传递键或键值对以删除所需的元素。
hashTable.remove("Ram");
or
hashTable.remove("Ram", 94.6);
示例
import java.util.Hashtable;
public class RemovingElements {
public static void main(String args[]) {
Hashtable hashTable = new Hashtable();
hashTable.put("Ram", 94.6);
hashTable.put("Rahim", 92);
hashTable.put("Robert", 85);
hashTable.put("Roja", 93);
hashTable.put("Raja", 75);
System.out.println("Contents of the hash table :"+hashTable);
hashTable.remove("Ram");
System.out.println("Contents of the hash table after deleting the specified elements :"+hashTable);
}
}
输出
Contents of the hash table :{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
Contents of the hash table after deleting the specified elements :{Rahim = 92, Roja = 93, Raja = 75, Robert = 85}
检索哈希表中的值
您可以使用 get() 方法检索特定键的值。如果将特定元素的键作为此方法的参数传递,则它将返回指定键的值(作为对象)。如果哈希表在指定的键下不包含任何元素,则返回 null。
您可以使用此方法检索哈希表中的值。
示例
import java.util.Hashtable;
public class RetrievingElements {
public static void main(String args[]) {
Hashtable hashTable = new Hashtable();
hashTable.put("Ram", 94.6);
hashTable.put("Rahim", 92);
hashTable.put("Robert", 85);
hashTable.put("Roja", 93);
hashTable.put("Raja", 75);
Object ob = hashTable.get("Ram");
System.out.println("Value of the specified key :"+ ob);
}
}
输出
Value of the specified key :94.6
遍历哈希表
HashTable 类提供了一个名为 keys() 的方法,该方法返回一个枚举对象,其中包含哈希表中的所有键。
使用此方法获取键,并使用 get() 方法检索每个键的值。
Enumeration(接口)的 hasMoreElements() 方法如果枚举对象还有更多元素则返回 true。您可以使用此方法运行循环。
示例
import java.util.Enumeration;
import java.util.Hashtable;
public class Loopthrough {
public static void main(String args[]) {
String str;
Hashtable hashTable = new Hashtable();
hashTable.put("Ram", 94.6);
hashTable.put("Rahim", 92);
hashTable.put("Robert", 85);
hashTable.put("Roja", 93);
hashTable.put("Raja", 75);
Enumeration keys = hashTable.keys();
System.out.println("Contents of the hash table are :");
while(keys.hasMoreElements()) {
str = (String) keys.nextElement();
System.out.println(str + ": " + hashTable.get(str));
}
}
}
输出
Contents of the hash table are : Rahim: 92 Roja: 93 Raja: 75 Ram: 94.6 Robert: 85
合并两个哈希表
HashTable 类的 putAll() 方法接受一个 map 对象作为参数,将其所有内容添加到当前哈希表中并返回结果。
使用此方法,您可以合并两个哈希表的内容。
示例
import java.util.Hashtable;
public class JoiningTwoHashTables {
public static void main(String args[]) {
String str;
Hashtable hashTable1 = new Hashtable();
hashTable1.put("Ram", 94.6);
hashTable1.put("Rahim", 92);
hashTable1.put("Robert", 85);
hashTable1.put("Roja", 93);
hashTable1.put("Raja", 75);
System.out.println("Contents of the 1st hash table :"+hashTable1);
Hashtable hashTable2 = new Hashtable();
hashTable2.put("Sita", 84.6);
hashTable2.put("Gita", 89);
hashTable2.put("Ramya", 86);
hashTable2.put("Soumaya", 96);
hashTable2.put("Sarmista", 92);
System.out.println("Contents of the 2nd hash table :"+hashTable2);
hashTable1.putAll(hashTable2);
System.out.println("Contents after joining the two hash tables: "+hashTable1);
}
}
输出
Contents of the 1st hash table :{Rahim = 92, Roja = 93, Raja = 75, Ram = 94.6, Robert = 85}
Contents of the 2nd hash table :{Sarmista = 92, Soumaya = 96, Sita = 84.6, Gita = 89, Ramya = 86}
Contents after joining the two hash tables: {Soumaya = 96, Robert = 85, Ram = 94.6, Sarmista = 92,
Raja = 75, Sita = 84.6, Roja = 93, Gita = 89, Rahim = 92, Ramya = 86}
创建二叉树
树是一种数据结构,其元素/节点彼此连接,类似于链表。但是,与链表不同的是,树是一种非线性数据结构,其中树中的每个元素/节点都连接到多个节点(以分层方式)。
在树中,没有任何前置元素的节点,即树顶部的节点,称为根节点。每棵树只包含一个根节点。
除根节点外的任何节点都向上有一条边连接到称为父节点的节点。
由其向下边连接的给定节点下方的节点称为其子节点。
没有子节点的节点称为叶节点。
每个节点最多只有 0 个、1 个或 2 个子节点的树称为二叉树。二叉树兼具有序数组和链表的优点,因为搜索速度与排序数组一样快,插入或删除操作速度与链表一样快。
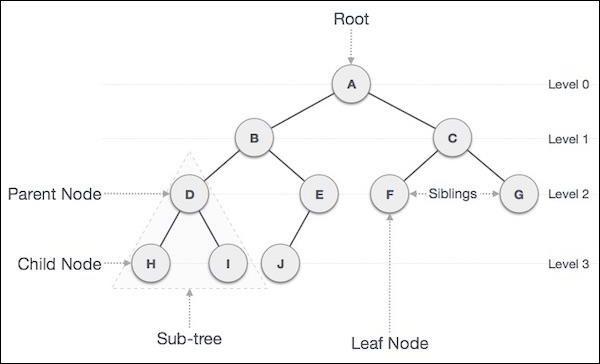
在 Java 中创建二叉树
要创建/实现二叉树,请创建一个 Node 类,该类将存储int值并保留对每个子节点的引用,创建三个变量。
两个 Node 类型的变量用于存储左节点和右节点,一个整数类型的变量用于存储数据。然后从另一个类尝试创建节点,这样在分层方式中,任何节点都不应该超过 2 个子节点。
示例
以下是创建二叉树的示例,这里我们创建了一个 Node 类,其中包含数据、左节点和右节点的变量,包括 setter 和 getter 方法来设置和检索它们的值。
import java.util.LinkedList;
import java.util.Queue;
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class CreatingBinaryTree {
public static void main(String[] args){
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("Binary Tree Created Pre-order of its elements is: ");
preOrder(node);
}
public static void preOrder(Node root){
if(root !=null){
System.out.println(root.data);
preOrder(root.leftNode);
preOrder(root.rightNode);
}
}
}
输出
Binary Tree Created Pre-order of its elements is: 50 60 45 64 60 45 64
向树中插入键
没有特定的规则将元素插入二叉树,您可以根据需要插入节点。
插入节点时应记住的唯一一点是,在二叉树中,每个节点最多只能有两个子节点。
因此,要将节点插入树中,
逐层遍历每个节点,检查它是否有左节点和右节点。
如果任何节点同时具有左节点和右节点,则不能插入另一个节点,因为二叉树中的节点最多只能有两个子节点,将这些值添加到队列中并继续。
如果任何节点没有左节点或右节点,则创建一个新节点并将其添加到那里。
简而言之,将节点插入没有左子树或右子树或两者都没有的父节点。
示例
import java.util.LinkedList;
import java.util.Queue;
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class InsertingElements {
public static int[] insertElement(int[] myArray, int pos, int data) {
int j = myArray.length;
int lastElement = myArray[j-1];
for(int i = (j-2); i >= (pos-1); i--) {
myArray[i+1] = myArray[i];
}
myArray[pos-1] = data;
int[] resultArray = new int[j+1];
for(int i = 0; i < myArray.length; i++) {
resultArray[i] = myArray[i];
}
resultArray[resultArray.length-1] = lastElement;
return resultArray;
}
public static void main(String args[]){
int[] myArray = {10, 20, 30, 45, 96, 66};
int pos = 3;
int data = 10005;
int[] result = insertElement(myArray, pos, data);
for(int i = 0; i < result.length; i++){
System.out.println(result[i]);
}
}
}
输出
10 20 10005 30 45 96 66
树的中序遍历
在此遍历方法中,首先访问左子树,然后访问根,最后访问右子树。我们应该始终记住,每个节点本身都可以表示一个子树。
如果以中序遍历二叉树,则输出将以升序产生排序的键值。
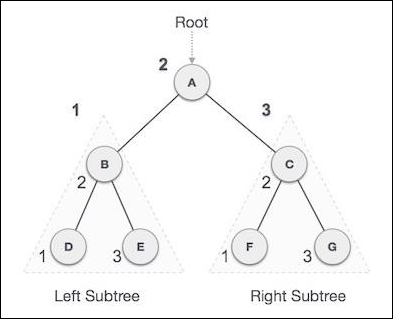
我们从A开始,按照中序遍历,我们移动到它的左子树B。B也以中序遍历。这个过程一直持续到访问所有节点。这棵树的中序遍历输出将是:
D → B → E → A → F → C → G
算法
直到所有节点都被遍历:
Step 1: Recursively traverse left subtree. Step 2: Visit root node. Step 3: Recursively traverse right subtree.
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class InOrderBinaryTree {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("inorder arrangement of given elements: ");
inOrder(node);
}
public static void inOrder(Node root) {
if(root !=null) {
inOrder(root.leftNode);
System.out.println(root.data);
inOrder(root.rightNode);
}
}
}
输出
inorder arrangement of given elements: 45 60 64 50 45 60 64
树的前序遍历
在此遍历方法中,首先访问根节点,然后访问左子树,最后访问右子树。
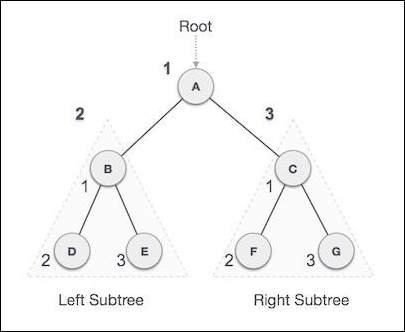
我们从A开始,按照前序遍历,我们首先访问A本身,然后移动到它的左子树B。B也以前序遍历。这个过程一直持续到访问所有节点。这棵树的前序遍历输出将是:
A → B → D → E → C → F → G
算法
直到所有节点都被遍历:
Step 1: Visit root node. Step 2: Recursively traverse left subtree. Step 3: Recursively traverse right subtree.
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class PreOrderBinaryTree {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("pre-order arrangement of given elements: ");
preOrder(node);
}
public static void preOrder(Node root) {
if(root !=null) {
System.out.println(root.data);
preOrder(root.leftNode);
preOrder(root.rightNode);
}
}
}
输出
pre-order arrangement of given elements: 50 60 45 64 60 45 64
树的后序遍历
在此遍历方法中,根节点最后访问,因此得名。我们首先遍历左子树,然后遍历右子树,最后遍历根节点。
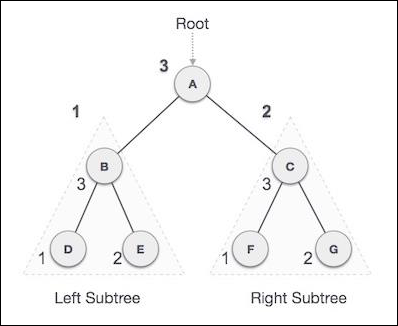
我们从A开始,按照后序遍历,首先访问左子树B。B也进行后序遍历。这个过程持续到所有节点都被访问为止。这个树的后序遍历输出结果是:
D → E → B → F → G → C → A
算法
直到所有节点都被遍历:
Step 1 − Recursively traverse left subtree. Step 2 − Recursively traverse right subtree. Step 3 − Visit root node.
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class PostOrderBinaryTree {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("post-order arrangement of given elements: ");
postOrder(node);
}
public static void postOrder(Node root) {
if(root !=null) {
postOrder(root.leftNode);
postOrder(root.rightNode);
System.out.println(root.data);
}
}
}
输出
post-order arrangement of given elements: 45 64 60 45 64 60 50
搜索树中的最小值
要查找一棵树的最小值(无子节点),比较左节点和右节点,取较大值(存储在max中),然后将其与根节点的值进行比较。
如果结果(min)较小,则它是最小值;否则,根节点是树的最小值。
要获取整个二叉树的最小值,获取左子树的最小值、右子树的最小值和根节点的值。现在比较这三个值,其中较小的值就是树的最小值。
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class MinValueInBinaryTree {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("Minimum value is "+minimumValue(node));
}
public static int minimumValue(Node root) {
int min = 10000;
if(root!=null) {
int lMin = minimumValue(root.leftNode);
int rMin = minimumValue(root.rightNode);;
if(lMin>rMin) {
min = lMin;
} else {
min = rMin;
}
if(root.data<min) {
min = root.data;
}
}
return min;
}
}
输出
Minimum value is 50
搜索树中的最大值
要查找一棵树的最大值(无子节点),比较左节点和右节点,取较大值(存储在max中),然后将其与根节点的值进行比较。
如果结果(max)较大,则它是树的最大值;否则,根节点是树的最大值。
要获取整个二叉树的最大值,获取左子树的最大值、右子树的最大值和根节点的值。现在比较这三个值,其中较大的值就是树的最大值。
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class MaxValueInBinaryTree {
public static void main(String[] args){
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("Maximum value is "+maximumValue(node));
}
public static int maximumValue(Node root) {
int max = 0;
if(root!=null) {
int lMax = maximumValue(root.leftNode);
int rMax = maximumValue(root.rightNode);;
if(lMax>rMax){
max = lMax;
} else {
max = rMax;
}
if(root.data>max) {
max = root.data;
}
}
return max;
}
}
输出
Maximum value is 64
在树中搜索值
要搜索给定树是否包含特定元素。将其与树中的每个元素进行比较,如果找到,则显示一条消息,说明找到了元素。
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class SeachingValue {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
System.out.println("Pre order of the above created tree :");
preOrder(node);
System.out.println();
int data = 60;
boolean b = find(node, data);
if(b) {
System.out.println("Element found");
} else {
System.out.println("Element not found");
}
}
public static void preOrder(Node root) {
if(root !=null) {
System.out.print(root.data+" ");
preOrder(root.leftNode);
preOrder(root.rightNode);
}
}
public static boolean find(Node root, int data) {
if(root == null) {
return false;
}
if(root.getData() == data) {
return true;
}
return find(root.getleftNode(), data)||find(root.getRightNode(), data);
}
}
输出
Pre order of the above created tree : 50 60 45 64 60 45 64 Element found
删除树中的叶子节点
遍历树中的每个节点,验证它是否有左子节点、右子节点或两者都有。如果它没有任何子节点,则删除该特定节点。
示例
class Node{
int data;
Node leftNode, rightNode;
Node() {
leftNode = null;
rightNode = null;
this.data = data;
}
Node(int data) {
leftNode = null;
rightNode = null;
this.data = data;
}
int getData() {
return this.data;
}
Node getleftNode() {
return this.leftNode;
}
Node getRightNode() {
return this.leftNode;
}
void setData(int data) {
this.data = data;
}
void setleftNode(Node leftNode) {
this.leftNode = leftNode;
}
void setRightNode(Node rightNode) {
this.leftNode = rightNode;
}
}
public class RemovingLeaf {
public static void main(String[] args) {
Node node = new Node(50);
node.leftNode = new Node(60);
node.leftNode.leftNode = new Node(45);
node.leftNode.rightNode = new Node(64);
node.rightNode = new Node(60);
node.rightNode.leftNode = new Node(45);
node.rightNode.rightNode = new Node(64);
node.leftNode.leftNode.leftNode = new Node(96);
System.out.println("Contents of the tree:");
preOrder(node);
removeLeaves(node);
System.out.println();
System.out.println("Contents of the tree after removing leafs:");
preOrder(node);
}
public static void removeLeaves(Node node) {
if (node.leftNode != null) { // tests left root
if (node.leftNode.leftNode == null && node.leftNode.rightNode == null) {
node.leftNode = null; // delete
} else {
removeLeaves(node.leftNode);
}
}
}
public static void preOrder(Node root) {
if(root !=null) {
System.out.print(root.data+" ");
preOrder(root.leftNode);
preOrder(root.rightNode);
}
}
}
输出
Contents of the tree: 50 60 45 96 64 60 45 64 Contents of the tree after removing leafs: 50 60 45 64 60 45 64
Java数据结构 - AVL树
如果二叉搜索树的输入以排序(升序或降序)的方式出现会怎样?它将如下所示:
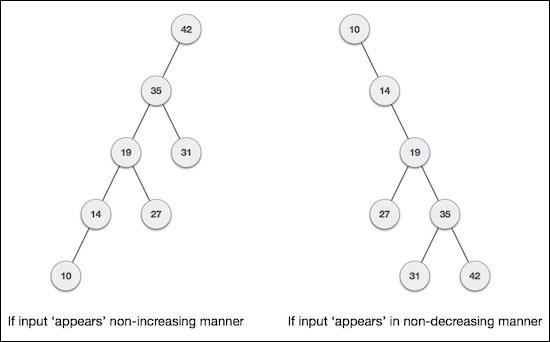
可以观察到,BST的最坏情况性能最接近线性搜索算法,即Ο(n)。在实时数据中,我们无法预测数据模式及其频率。因此,需要平衡现有的BST。
以其发明者Adelson、Velski和Landis的名字命名,AVL树是高度平衡的二叉搜索树。AVL树检查左右子树的高度,并确保其差值不超过1。这个差值称为平衡因子。
在这里,我们看到第一棵树是平衡的,接下来的两棵树是不平衡的:
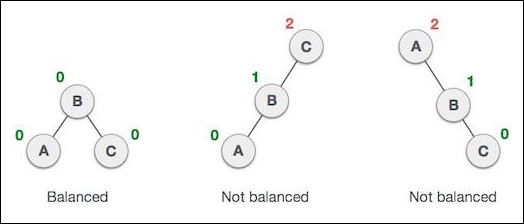
在第二棵树中,C的左子树高度为2,右子树高度为0,因此差值为2。在第三棵树中,A的右子树高度为2,而左子树缺失,因此为0,差值再次为2。AVL树只允许差值(平衡因子)为1。
BalanceFactor = height(left-sutree) − height(right-sutree)
如果左右子树的高度差大于1,则使用一些旋转技术来平衡树。
AVL旋转Java
为了平衡自身,AVL树可以执行以下四种旋转:
- 左旋转
- 右旋转
- 左-右旋转
- 右-左旋转
前两种旋转是单旋转,后两种旋转是双旋转。要使树不平衡,至少需要高度为2的树。通过这棵简单的树,让我们逐一了解它们。
左旋转
如果在右子树的右子树中插入节点时树变得不平衡,则执行单左旋转:
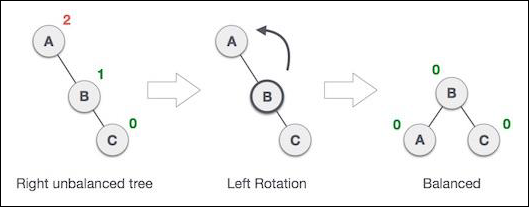
在我们的示例中,节点A变得不平衡,因为在A的右子树中插入了一个节点。我们通过使A成为B的左子树来执行左旋转。
右旋转
如果在左子树的左子树中插入节点,则AVL树可能变得不平衡。然后树需要右旋转。
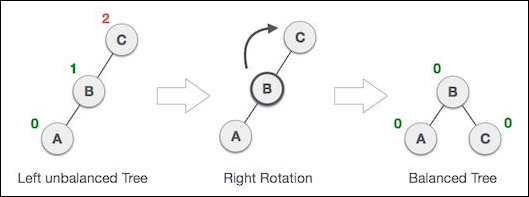
如图所示,通过执行右旋转,不平衡的节点成为其左子节点的右子节点。
左-右旋转
双旋转是已经解释过的旋转版本的稍微复杂一些的版本。为了更好地理解它们,我们应该注意旋转时执行的每个动作。让我们首先检查如何执行左-右旋转。左-右旋转是左旋转后跟右旋转的组合。
| 状态 | 动作 |
|---|---|
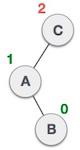 |
在左子树的右子树中插入了A节点。这使得C成为不平衡节点。这些场景导致AVL树执行左-右旋转。 |
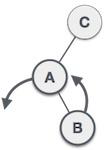 |
我们首先对C的左子树执行左旋转。这使得A成为B的左子树。 |
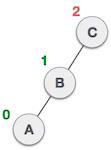 |
节点C仍然不平衡,但是现在,这是因为左子树的左子树。 |
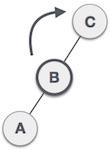 |
我们现在将对树进行右旋转,使B成为这个子树的新根节点。C现在成为其自身左子树的右子树。 |
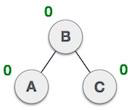 |
树现在已经平衡。 |
右-左旋转
第二种双旋转是右-左旋转。它是右旋转后跟左旋转的组合。
| 状态 | 动作 |
|---|---|
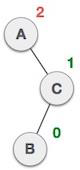 |
在右子树的左子树中插入了一个节点。这使得A成为一个不平衡节点,平衡因子为2。 |
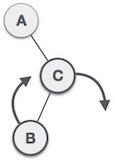 |
首先,我们沿C节点执行右旋转,使C成为其自身左子树B的右子树。现在,B成为A的右子树。 |
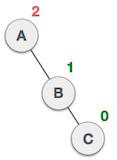 |
节点A仍然不平衡,因为其右子树的右子树,需要左旋转。 |
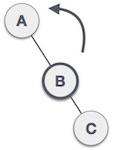 |
通过使B成为子树的新根节点来执行左旋转。A成为其右子树B的左子树。 |
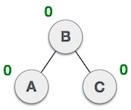 |
树现在已经平衡。 |
广度优先搜索 (BFS)
图是对象集合的图形表示,其中一些对象对通过链接连接。相互连接的对象由称为顶点的点表示,连接顶点的链接称为边。
形式上,图是一对集合(V, E),其中V是顶点集合,E是连接顶点对的边集合。看看下面的图:
在上图中,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
广度优先搜索 (BFS)
广度优先搜索 (BFS) 算法以广度优先的方式遍历图,并使用队列来记住在任何迭代中遇到死胡同时要开始搜索的下一个顶点。
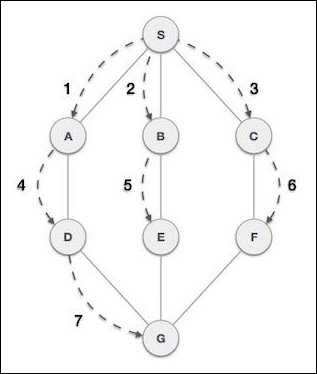
如上例所示,BFS算法首先从A到B到E到F遍历,然后到C和G,最后到D。它采用以下规则。
规则1 - 访问相邻的未访问顶点。将其标记为已访问。显示它。将其插入队列。
规则2 - 如果找不到相邻顶点,则从队列中删除第一个顶点。
规则3 - 重复规则1和规则2,直到队列为空。
| 步骤 | 遍历 | 描述 |
|---|---|---|
| 1 | 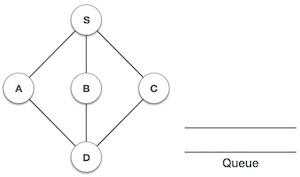 |
初始化队列。 |
| 2 | 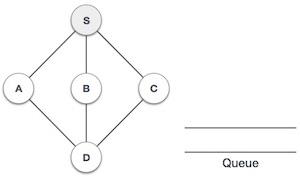 |
我们从访问S(起始节点)开始,并将其标记为已访问。 |
| 3 | 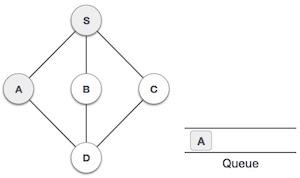 |
然后我们看到来自S的未访问相邻节点。在这个例子中,我们有三个节点,但按字母顺序我们选择A,将其标记为已访问并将其入队。 |
| 4 | 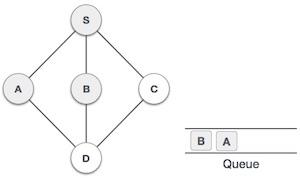 |
接下来,来自S的未访问相邻节点是B。我们将其标记为已访问并将其入队。 |
| 5 | 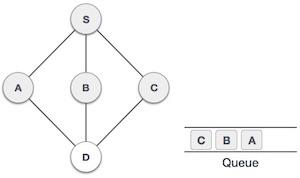 |
接下来,来自S的未访问相邻节点是C。我们将其标记为已访问并将其入队。 |
| 6 | 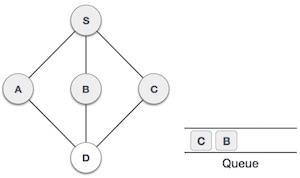 |
现在,S没有未访问的相邻节点了。所以,我们出队并找到A。 |
| 7 | 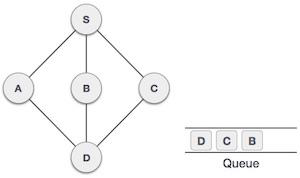 |
从A我们有D作为未访问的相邻节点。我们将其标记为已访问并将其入队。 |
在这个阶段,我们没有未标记(未访问)的节点了。但是根据算法,我们继续出队以获得所有未访问的节点。当队列为空时,程序结束。
深度优先搜索 (DFS)
深度优先搜索 (DFS) 算法以深度优先的方式遍历图,并使用堆栈来记住在任何迭代中遇到死胡同时要开始搜索的下一个顶点。
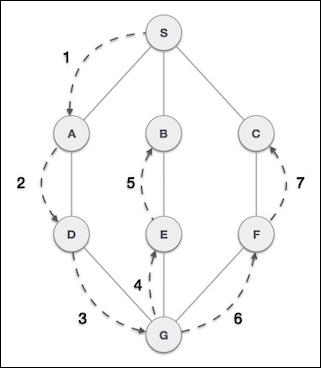
如上例所示,DFS算法首先从S到A到D到G到E到B遍历,然后到F,最后到C。它采用以下规则。
规则1 - 访问相邻的未访问顶点。将其标记为已访问。显示它。将其压入堆栈。
规则2 - 如果找不到相邻顶点,则从堆栈中弹出顶点。(它将弹出堆栈中的所有没有相邻顶点的顶点。)
规则3 - 重复规则1和规则2,直到堆栈为空。
| 步骤 | 遍历 | 描述 |
|---|---|---|
| 1 | 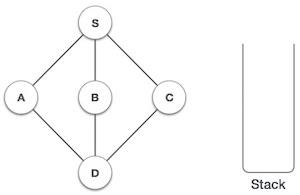 |
初始化堆栈。 |
| 2 | 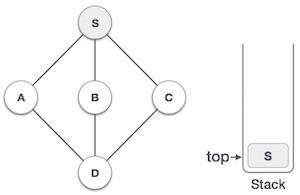 |
将S标记为已访问并将其放入堆栈。探索来自S的任何未访问的相邻节点。我们有三个节点,我们可以选择任何一个。在这个例子中,我们将按字母顺序取节点。 |
| 3 | 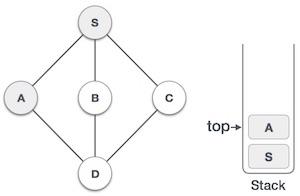 |
将A标记为已访问并将其放入堆栈。探索来自A的任何未访问的相邻节点。S和D都与A相邻,但我们只关注未访问的节点。 |
| 4 | 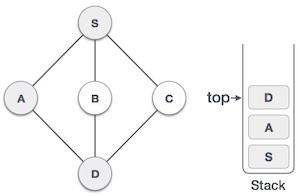 |
访问D,将其标记为已访问并将其放入堆栈。在这里,我们有B和C节点,它们与D相邻,并且都是未访问的。但是,我们将再次按字母顺序选择。 |
| 5 | 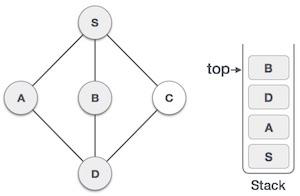 |
我们选择B,将其标记为已访问并将其放入堆栈。这里B没有任何未访问的相邻节点。所以,我们从堆栈中弹出B。 |
| 6 | 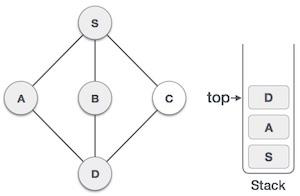 |
我们检查堆栈顶部以返回到前一个节点,并检查它是否有任何未访问的节点。在这里,我们发现D位于堆栈顶部。 |
| 7 | 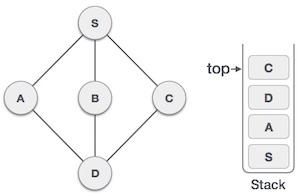 |
现在,来自D的唯一未访问的相邻节点是C。所以我们访问C,将其标记为已访问并将其放入堆栈。 |
最短路径算法
最短路径算法是从源节点(S)到目标节点(D)寻找最小成本路径的方法。在这里,我们将讨论Moore算法,也称为广度优先搜索算法。
Moore算法
标记源顶点S,并将其标记为i,并设置i = 0。
查找与标记为i的顶点相邻的所有未标记顶点。如果没有顶点连接到顶点S,则顶点D未连接到S。如果有顶点连接到S,则将其标记为i+1。
如果D已标记,则转到步骤4,否则转到步骤2以增加i = i+1。
找到最短路径的长度后停止。
迪克斯特拉算法
迪克斯特拉算法解决有向加权图G = (V, E)上的单源最短路径问题,其中所有边均为非负权值(即,对于每条边(u, v) Є E,都有w(u, v) ≥ 0)。
在下面的算法中,我们将使用一个函数Extract-Min(),它提取具有最小键值的节点。
算法:Dijkstra算法 (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
S := Ф
Q := G.V
while Q ≠ Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v.∏ := u
分析
该算法的复杂度完全取决于Extract-Min函数的实现。如果使用线性搜索实现Extract-Min函数,则该算法的复杂度为O(V2 + E)。
在此算法中,如果我们使用最小堆,Extract-Min()函数作用于最小堆,从Q返回具有最小键值的节点,则可以进一步降低该算法的复杂度。
示例
让我们考虑顶点1和9分别作为起点和终点顶点。最初,除起点顶点外,所有顶点均标记为∞,起点顶点标记为0。
| 顶点 | 初始值 | 步骤1 V1 | 步骤2 V3 | 步骤3 V2 | 步骤4 V4 | 步骤5 V5 | 步骤6 V7 | 步骤7 V8 | 步骤8 V6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
因此,顶点9到顶点1的最小距离为20。路径为:
1 → 3 → 7 → 8 → 6 → 9
此路径是根据前驱信息确定的。
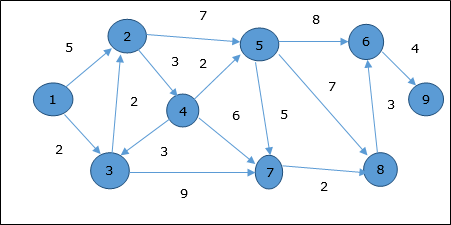
Bellman-Ford算法
该算法求解有向图G = (V, E)的单源最短路径问题,其中边权重可能为负值。此外,如果不存在任何负权环,则可以使用此算法查找最短路径。
算法:Bellman-Ford算法 (G, w, s)
for each vertex v Є G.V
v.d := ∞
v.∏ := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v.∏ := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
分析
第一个for循环用于初始化,运行O(V)次。下一个for循环对边进行|V - 1|次遍历,耗时O(E)。
因此,Bellman-Ford算法的运行时间为O(V, E)。
示例
以下示例逐步展示了Bellman-Ford算法的工作原理。此图具有负边,但不包含任何负环,因此可以使用此技术解决问题。
在初始化时,除源节点外,所有顶点均标记为∞,源节点标记为0。
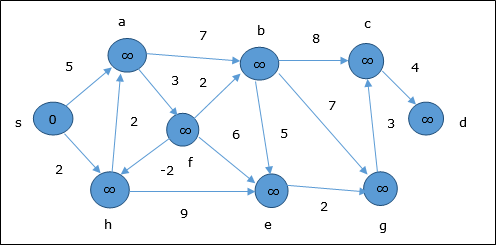
第一步,所有从源节点可达的顶点都将更新为最小成本。因此,顶点a和h被更新。
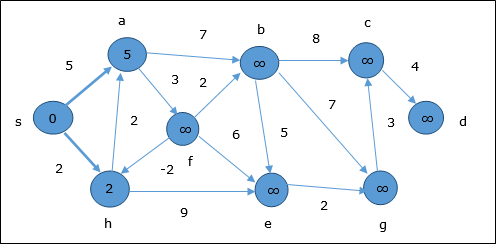
下一步,顶点a, b, f和e被更新。
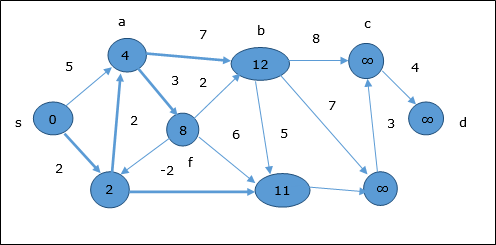
按照相同的逻辑,在此步骤中,顶点b, f, c和g被更新。
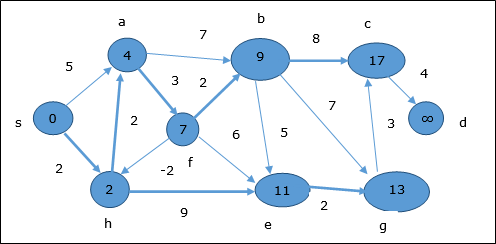
此处,顶点c和d被更新。
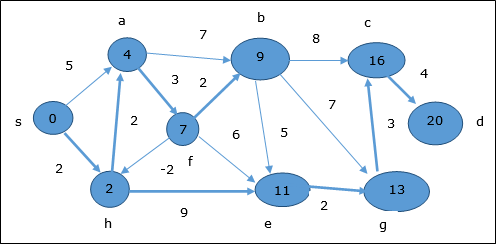
因此,顶点s和顶点d之间的最小距离为20。
根据前驱信息,路径为s → h → e → g → c → d
最小生成树 (MST)
在加权图中,最小生成树是指权重小于同图所有其他生成树的生成树。在现实情况下,此权重可以衡量为距离、拥塞、交通负荷或分配给边的任何任意值。
Java中的Prim算法
Prim算法(与克鲁斯卡尔算法一样)用于查找最小成本生成树,它使用贪心算法。Prim算法与最短路径优先算法类似。
与克鲁斯卡尔算法相反,Prim算法将节点视为单个树,并不断从给定图中向生成树添加新节点。
为了与克鲁斯卡尔算法进行对比并更好地理解Prim算法,我们将使用相同的示例:
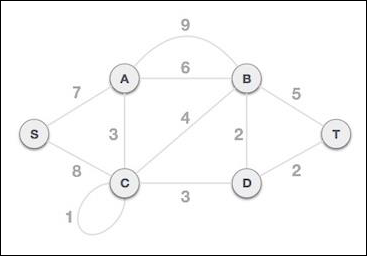
步骤1 - 删除所有环和并行边
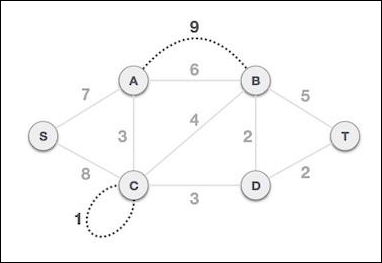
从给定图中删除所有环和并行边。对于并行边,保留关联成本最低的那一条,删除所有其他边。
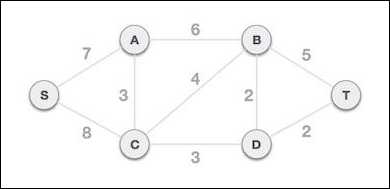
步骤2 - 选择任意节点作为根节点
在本例中,我们选择S节点作为Prim生成树的根节点。此节点是任意选择的,因此任何节点都可以作为根节点。有人可能会问为什么任何视频都可以是根节点。答案是,在生成树中包含图的所有节点,并且由于它是连通的,因此必须至少有一条边将它连接到树的其余部分。
步骤3 - 检查外出边并选择成本较低的那条边
选择根节点S后,我们看到S,A和S,C是两条权重分别为7和8的边。我们选择边S,A,因为它小于另一条边。
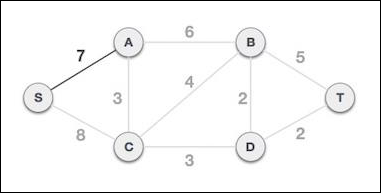
现在,树S-7-A被视为一个节点,我们检查从中引出的所有边。我们选择成本最低的那条边并将其包含在树中。
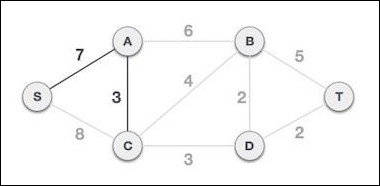
此步骤之后,形成S-7-A-3-C树。现在,我们将再次将其视为一个节点,并将再次检查所有边。但是,我们只选择成本最低的边。在本例中,C-3-D是新的边,它小于其他边的成本8、6、4等。
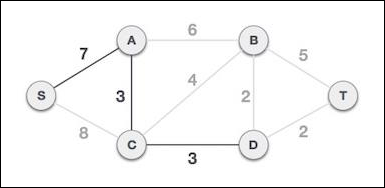
将节点D添加到生成树后,我们现在有两条从其引出的边具有相同的成本,即D-2-T和D-2-B。因此,我们可以添加其中任何一条。但是下一步将再次产生边2作为最低成本。因此,我们显示包含两条边的生成树。
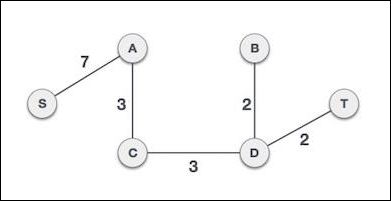
我们可能会发现,使用两种不同算法得到的同一图的输出生成树是相同的。
Java数据结构 - 克鲁斯卡尔算法
克鲁斯卡尔算法使用贪心算法来查找最小成本生成树。此算法将图视为森林,并将每个节点都视为单个树。只有当一条树的成本在所有可用选项中最低且不违反MST属性时,它才会连接到另一条树。
为了理解克鲁斯卡尔算法,让我们考虑以下示例:
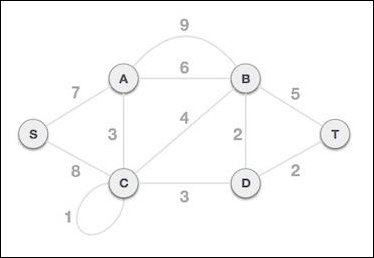
步骤1 - 删除所有环和并行边
从给定图中删除所有环和并行边。
对于并行边,保留关联成本最低的那一条,删除所有其他边。
步骤2 - 按权重递增顺序排列所有边
下一步是创建一个边和权重的集合,并按权重(成本)递增顺序排列它们。
| B,D | D,T | A,C | C,D | C,B | B,T | A,B | S,A | S,C |
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
步骤3 - 添加权重最低的边
现在我们开始从权重最低的边开始向图中添加边。在整个过程中,我们将不断检查生成树属性是否保持不变。如果通过添加一条边,生成树属性不成立,那么我们将考虑不将该边包含在图中。

最低成本为2,相关的边为B,D和D,T。我们添加它们。添加它们不会违反生成树属性,因此我们继续选择下一条边。
下一个成本为3,相关的边为A,C和C,D。我们再次添加它们:
表中的下一个成本为4,我们观察到添加它会在图中创建一个环。
我们忽略它。在此过程中,我们将忽略/避免所有创建环的边。
我们观察到成本为5和6的边也会创建环。我们忽略它们并继续。
现在只剩下一个节点需要添加。在两个可用的最低成本边7和8之间,我们将添加成本为7的边。
通过添加边S,A,我们包含了图的所有节点,现在我们有了最小成本生成树。
Java数据结构 - 冒泡排序
排序是指以特定格式排列数据。排序算法指定以特定顺序排列数据的方式。最常见的顺序是数值顺序或字典顺序。
排序的重要性在于,如果数据以排序方式存储,则可以将数据搜索优化到非常高的水平。排序还用于以更易读的格式表示数据。以下是现实生活中排序的一些示例。
电话簿 - 电话簿按姓名排序存储人们的电话号码,以便可以轻松搜索姓名。
字典 - 字典按字母顺序存储单词,以便可以轻松搜索任何单词。
就地排序和非就地排序
排序算法可能需要一些额外的空间来比较和临时存储一些数据元素。这些算法不需要任何额外空间,排序据说发生在原地,或者例如,在数组本身内。这称为就地排序。冒泡排序就是一个就地排序的例子。
但是,在某些排序算法中,程序需要的空间大于或等于被排序的元素。使用等于或更多空间的排序称为非就地排序。归并排序就是一个非就地排序的例子。
Java中的冒泡排序
冒泡排序是一种简单的排序算法。这种排序算法是一种基于比较的算法,其中比较每对相邻元素,如果元素没有按顺序排列,则交换元素。这种算法不适用于大型数据集,因为它的平均和最坏情况复杂度为Ο(n2),其中n是项目数。
算法
我们假设list是一个包含n个元素的数组。我们进一步假设swap()函数交换给定数组元素的值。
Step 1: Assume i is the first element of the list then, compare the elements i and i+1. (first two elements of the array) Step 2: If the i (first element) is greater than the second (i+1) swap them. Step 3: Now, increment the i value and repeat the same.(for 2nd and 3rd elements) Step 4: Repeat this till the end of the array.
示例
import java.util.Arrays;
public class BubbleSort {
public static void main(String args[]) {
int[] myArray = {10, 20, 65, 96, 56};
System.out.println("Contents of the array before sorting : ");
System.out.println(Arrays.toString(myArray));
int n = myArray.length;
int temp = 0;
for(int i = 0; i<n-1; i++) {
for(int j = 0; j<n-1; j++) {
if (myArray[j] > myArray[j+1]) {
temp = myArray[i];
myArray[j] = myArray[j+1];
myArray[j+1] = temp;
}
}
}
System.out.println("Contents of the array after sorting : ");
System.out.println(Arrays.toString(myArray));
}
}
输出
Contents of the array before sorting : [10, 20, 65, 96, 56] Contents of the array after sorting : [10, 10, 20, 10, 20]
Java数据结构 - 选择排序
选择排序是一种简单的排序算法。这种排序算法是一种原地比较排序算法,它将列表分成两个部分:左端的有序部分和右端的无序部分。最初,有序部分为空,无序部分是整个列表。
从无序数组中选择最小的元素,并将其与最左边的元素交换,该元素成为有序数组的一部分。这个过程继续进行,无序数组边界向右移动一个元素。
该算法不适用于大型数据集,因为它的平均和最坏情况复杂度为Ο(n2),其中n是项目的数量。
算法
Step 1: Set MIN to location 0 in the array. Step 2: Search the minimum element in the list. Step 3: Swap with value at location MIN. Step 4: Increment MIN to point to next element. Step 5: Repeat until list is sorted.
示例
import java.util.Arrays;
public class SelectionSort {
public static void main(String args[]) {
int myArray[] = {10, 20, 25, 63, 96, 57};
int n = myArray.length;
System.out.println("Contents of the array before sorting : ");
System.out.println(Arrays.toString(myArray));
for (int i=0 ;i< n-1; i++) {
int min = i;
for (int j = i+1; j<n; j++) {
if (myArray[j] < myArray[min]) {
min = j;
}
}
int temp = myArray[min];
myArray[min] = myArray[i];
myArray[i] = temp;
}
System.out.println("Contents of the array after sorting : ");
System.out.println(Arrays.toString(myArray));
}
}
输出
Contents of the array before sorting : [10, 20, 25, 63, 96, 57] Contents of the array after sorting : [10, 20, 25, 57, 63, 96]
Java数据结构 - 插入排序
这是一种原地比较排序算法。这里,维护一个子列表,该子列表始终是有序的。例如,数组的下半部分保持有序。要插入到此有序子列表中的元素必须找到其适当的位置,然后将其插入到该位置。因此得名插入排序。
对数组进行顺序搜索,并将无序项移动并插入到有序子列表(在同一数组中)。该算法不适用于大型数据集,因为它的平均和最坏情况复杂度为Ο(n2),其中n是项目的数量。
算法
Step 1: If it is the first element, it is already sorted. return 1; Step 2: Pick next element. Step 3: Compare with all elements in the sorted sub-list. Step 4: Shift all the elements in the sorted sub-list that is greater than the value to be sorted. Step 5: Insert the value. Step 6: Repeat until list is sorted.
示例
import java.util.Arrays;
public class InsertionSort {
public static void main(String args[]) {
int myArray[] = {10, 20, 25, 63, 96, 57};
int size = myArray.length;
System.out.println("Contents of the array before sorting : ");
System.out.println(Arrays.toString(myArray));
for (int i = 1 ;i< size; i++) {
int val = myArray[i];
int pos = i;
while(myArray[pos-1]>val && pos>0) {
myArray[pos] = myArray[pos-1];
pos = pos-1;
}
myArray[pos] = val;
}
System.out.println("Contents of the array after sorting : ");
System.out.println(Arrays.toString(myArray));
}
}
输出
Contents of the array before sorting : [10, 20, 25, 63, 96, 57] Contents of the array after sorting : [10, 20, 25, 57, 63, 96]
Java数据结构 - 归并排序
归并排序是一种基于分治技术的排序技术。其最坏情况时间复杂度为Ο(n log n),是广受推崇的算法之一。
归并排序首先将数组分成相等的两半,然后以有序的方式将它们合并。
算法
归并排序不断将列表分成相等的两半,直到无法再分割为止。根据定义,如果列表中只有一个元素,则它已排序。然后,归并排序合并较小的已排序列表,同时保持新列表也已排序。
Step 1: if it is only one element in the list it is already sorted, return. Step 2: divide the list recursively into two halves until it can no more be divided. Step 3: merge the smaller lists into new list in sorted order.
示例
import java.util.Arrays;
public class MergeSort {
int[] array = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
public void merge(int low, int mid, int high) {
int l1, l2, i, b[] = new int[array.length];
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(array[l1] <= array[l2]) {
b[i] = array[l1++];
} else
b[i] = array[l2++];
}
while(l1 <= mid) {
b[i++] = array[l1++];
}
while(l2 <= high) {
b[i++] = array[l2++];
}
for(i = low; i <= high; i++) {
array[i] = b[i];
}
}
public void sort(int low, int high) {
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merge(low, mid, high);
} else {
return;
}
}
public static void main(String args[]) {
MergeSort obj = new MergeSort();
int max = obj.array.length-1;
System.out.println("Contents of the array before sorting : ");
System.out.println(Arrays.toString(obj.array));
obj.sort(0, max);
System.out.println("Contents of the array after sorting : ");
System.out.println(Arrays.toString(obj.array));
}
}
输出
[10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0] Contents of the array after sorting : [0, 10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
Java数据结构 - 快速排序
快速排序是一种高效的排序算法,它基于将数据数组划分成较小的数组。一个大的数组被划分为两个数组,一个数组包含小于指定值(例如,枢轴)的值,基于该值进行划分,另一个数组包含大于枢轴值的值。
快速排序划分一个数组,然后递归调用自身两次以对两个生成的子数组进行排序。该算法对于大型数据集非常高效,因为它的平均和最坏情况复杂度为Ο(n2),其中n是项目的数量。
算法
基于我们对快速排序中划分的理解,我们现在将尝试为其编写一个算法,如下所示:
Step 1: Choose the highest index value has pivot. Step 2: Take two variables to point left and right of the list excluding pivot. Step 3: left points to the low index. Step 4: right points to the high. Step 5: while value at left is less than pivot move right. Step 6: while value at right is greater than pivot move left. Step 7: if both step 5 and step 6 does not match swap left and right. Step 8: if left ≥ right, the point where they met is new pivot.
快速排序算法
使用枢轴算法递归地,我们最终得到尽可能小的分区。然后对每个分区进行快速排序处理。我们对快速排序的递归算法定义如下:
Step 1: Make the right-most index value pivot. Step 2: partition the array using pivot value. Step 3: quicksort left partition recursively. Step 4: quicksort right partition recursively.
示例
import java.util.Arrays;
public class QuickSortExample {
int[] intArray = {4,6,3,2,1,9,7};
void swap(int num1, int num2) {
int temp = intArray[num1];
intArray[num1] = intArray[num2];
intArray[num2] = temp;
}
int partition(int left, int right, int pivot) {
int leftPointer = left -1;
int rightPointer = right;
while(true) {
while(intArray[++leftPointer] < pivot) {
// do nothing
}
while(rightPointer > 0 && intArray[--rightPointer] > pivot) {
// do nothing
}
if(leftPointer >= rightPointer) {
break;
} else {
swap(leftPointer,rightPointer);
}
}
swap(leftPointer,right);
// System.out.println("Updated Array: ");
return leftPointer;
}
void quickSort(int left, int right) {
if(right-left <= 0) {
return;
} else {
int pivot = intArray[right];
int partitionPoint = partition(left, right, pivot);
quickSort(left,partitionPoint-1);
quickSort(partitionPoint+1,right);
}
}
public static void main(String[] args) {
QuickSortExample sort = new QuickSortExample();
int max = sort.intArray.length;
System.out.println("Contents of the array :");
System.out.println(Arrays.toString(sort.intArray));
sort.quickSort(0, max-1);
System.out.println("Contents of the array after sorting :");
System.out.println(Arrays.toString(sort.intArray));
}
}
输出
Contents of the array : [4, 6, 3, 2, 1, 9, 7] Contents of the array after sorting : [1, 2, 3, 4, 6, 7, 9]
Java数据结构 - 堆排序
堆是一种树,具有特定条件,即节点的值大于(或小于)其子节点的值。堆排序是一种排序,我们使用二叉堆对数组的元素进行排序。
算法
Step 1: Create a new node at the end of heap. Step 2: Assign new value to the node. Step 3: Compare the value of this child node with its parent. Step 4: If value of parent is less than child, then swap them. Step 5: Repeat step 3 & 4 until Heap property holds.
示例
import java.util.Arrays;
import java.util.Scanner;
public class Heapsort {
public static void heapSort(int[] myArray, int length) {
int temp;
int size = length-1;
for (int i = (length / 2); i >= 0; i--) {
heapify(myArray, i, size);
}
for(int i = size; i>=0; i--) {
temp = myArray[0];
myArray[0] = myArray[size];
myArray[size] = temp;
size--;
heapify(myArray, 0, size);
}
System.out.println(Arrays.toString(myArray));
}
public static void heapify (int [] myArray, int i, int heapSize) {
int a = 2*i;
int b = 2*i+1;
int largestElement;
if (a<= heapSize && myArray[a] > myArray[i]) {
largestElement = a;
} else {
largestElement = i;
}
if (b <= heapSize && myArray[b] > myArray[largestElement]) {
largestElement = b;
}
if (largestElement != i) {
int temp = myArray[i];
myArray[i] = myArray[largestElement];
myArray[largestElement] = temp;
heapify(myArray, largestElement, heapSize);
}
}
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter the size of the array :: ");
int size = scanner.nextInt();
System.out.println("Enter the elements of the array :: ");
int[] myArray = new int[size];
for(int i = 0; i<size; i++) {
myArray[i] = scanner.nextInt();
}
heapSort(myArray, size);
}
}
输出
Enter the size of the array :: 5 Enter the elements of the array :: 45 125 44 78 1 [1, 44, 45, 78, 125]
Java数据结构 - 线性查找
线性查找是一种非常简单的搜索算法。在这种类型的搜索中,对所有项目逐个进行顺序搜索。检查每个项目,如果找到匹配项,则返回该特定项目,否则搜索将继续到数据集合的末尾。
算法
线性查找。(数组A,值x)
Step 1: Get the array and the element to search. Step 2: Compare value of the each element in the array to the required value. Step 3: In case of match print element found.
示例
public class LinearSearch {
public static void main(String args[]) {
int array[] = {10, 20, 25, 63, 96, 57};
int size = array.length;
int value = 63;
for (int i=0 ;i< size-1; i++) {
if(array[i]==value) {
System.out.println("Index of the required element is :"+ i);
}
}
}
}
输出
Index of the required element is :3
Java数据结构 - 二分查找
二分查找是一种快速的搜索算法,运行时间复杂度为Ο(log n)。该搜索算法基于分治的原理。为了使该算法正常工作,数据集合应按排序形式排列。
二分查找通过比较集合中最中间的项目来查找特定项目。如果发生匹配,则返回项目的索引。如果中间项大于该项,则在中间项左侧的子数组中搜索该项。否则,在中间项右侧的子数组中搜索该项。此过程也继续在子数组上进行,直到子数组的大小减小到零。
示例
public class BinarySearch {
public static void main(String args[]) {
int array[] = {10, 20, 25, 57, 63, 96};
int size = array.length;
int low = 0;
int high = size-1;
int value = 25;
int mid = 0;
mid = low +(high-low)/2;
while(low<=high) {
if(array[mid] == value) {
System.out.println(mid);
break;
} else if(array[mid]<value)
low = mid+1;
else high = mid - 1;
}
mid = (low+high)/2;
}
}
输出
2
Java数据结构 - 递归
一些计算机编程语言允许模块或函数调用自身。这种技术称为递归。在递归中,函数α要么直接调用自身,要么调用一个函数β,而β又调用原始函数α。函数α称为递归函数。
int sampleMethod(int value) {
if(value < 1) {
return;
}
sampleMethod(value - 1);
System.out.println(value);
}
属性
递归函数可能会像循环一样无限运行。为了避免递归函数无限运行,递归函数必须具有两个属性:
基本条件 - 必须至少有一个基本条件,当满足此条件时,函数停止递归调用自身。
递进方法 - 递归调用应该以这样的方式进行,每次递归调用都更接近基本条件。
实现
许多编程语言通过堆栈来实现递归。通常,每当一个函数(调用者)调用另一个函数(被调用者)或自身作为被调用者时,调用者函数将执行控制权转移给被调用者。此转移过程可能还涉及将一些数据从调用者传递给被调用者。
这意味着,调用者函数必须暂时挂起其执行,并在执行控制权从被调用者函数返回时恢复。在这里,调用者函数需要从其暂停执行的点开始精确执行。它还需要它正在处理的完全相同的数据值。为此,将为调用者函数创建一个激活记录(或堆栈帧)。
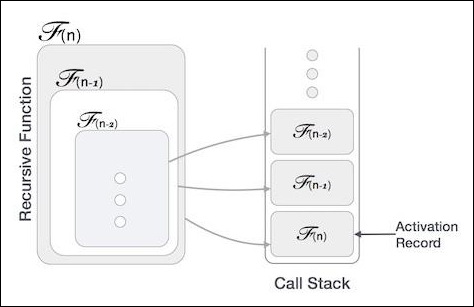
此激活记录保留有关局部变量、形式参数、返回地址以及传递给调用者函数的所有信息。
递归分析
有人可能会质疑为什么要使用递归,因为可以使用迭代来完成相同的任务。第一个原因是,递归使程序更易于阅读,并且由于最新的增强型 CPU 系统,递归比迭代更有效。
时间复杂度
对于迭代,我们采用迭代次数来计算时间复杂度。同样,对于递归,假设一切都是常数,我们试图找出递归调用的次数。对函数的调用为Ο(1),因此递归调用 (n) 次使递归函数为Ο(n)。
空间复杂度
空间复杂度计算为模块执行需要多少额外空间。对于迭代,编译器几乎不需要任何额外空间。编译器不断更新迭代中使用的变量的值。但是对于递归,系统需要在每次递归调用时存储激活记录。因此,认为递归函数的空间复杂度可能高于迭代函数的空间复杂度。
Java数据结构 - 斐波那契数列
动态规划方法类似于分治法,它将问题分解成越来越小的子问题。但与分治法不同的是,这些子问题不是独立解决的。相反,这些较小子问题的结果会被记住并用于类似或重叠的子问题。
动态规划用于我们可以将问题分解成类似子问题的情况,以便可以重用其结果。这些算法主要用于优化。在解决当前子问题之前,动态算法将尝试检查先前解决的子问题的结果。子问题的解决方案被组合起来以实现最佳解决方案。
所以我们可以说:
问题应该能够分解成较小的重叠子问题。
可以使用较小子问题的最佳解决方案来实现最佳解决方案。
动态算法使用记忆化。
比较
与解决局部优化的贪婪算法相比,动态算法的目标是对问题进行整体优化。
与分治算法(其中解决方案被组合以实现整体解决方案)相比,动态算法使用较小子问题的输出,然后尝试优化较大的子问题。动态算法使用记忆化来记住已解决子问题的输出。
动态规划可以自顶向下和自底向上两种方式使用。当然,在大多数情况下,参考以前的解决方案输出比重新计算更便宜(就 CPU 周期而言)。
Java中的斐波那契数列
以下是使用动态规划技术在Java中解决斐波那契数列的方案。
示例
import java.util.Scanner;
public class Fibonacci {
public static int fibonacci(int num) {
int fib[] = new int[num + 1];
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < num + 1; i++) {
fib[i] = fib[i - 1] + fib[i - 2];
}
return fib[num];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("Enter a number :");
int num = sc.nextInt();
for (int i = 1; i <= num; i++) {
System.out.print(" "+fibonacci(i));
}
}
}
输出
1 1 2 3 5 8 13 21 34 55 89 144
Java数据结构 - 背包问题
以下是使用动态规划技术在Java中解决背包问题的方案。
示例
public class KnapsackExample {
static int max(int a, int b) {
return (a > b)? a : b;
}
public static int knapSack(int capacity, int[] items, int[] values, int numOfItems ) {
int i, w;
int [][]K = new int[numOfItems+1][capacity+1];
// Build table K[][] in bottom up manner
for (i = 0; i <= numOfItems; i++) {
for (w = 0; w <= capacity; w++) {
if (i==0 || w==0) {
K[i][w] = 0;
} else if (items[i-1] <= w) {
K[i][w] = max(values[i-1] + K[i-1][w-items[i-1]], K[i-1][w]);
} else {
K[i][w] = K[i-1][w];
}
}
}
return K[numOfItems][capacity];
}
public static void main(String args[]) {
int[] items = {12, 45, 67, 90, 45};
int numOfItems = items.length;
int capacity = 100;
int[] values = {1200, 4500, 6700, 9000, 4500};
int x = knapSack(capacity, items, values, numOfItems );
System.out.println(x);
}
}
输出
9000
贪心算法的组成部分
算法旨在为给定问题实现最佳解决方案。在贪婪算法方法中,决策是从给定的解决方案域中做出的。作为贪婪算法,选择似乎提供最佳解决方案的最接近的解决方案。
贪婪算法试图找到局部最优解,这最终可能导致全局最优解。但是,通常贪婪算法不会提供全局最优解。
贪心算法的组成部分
贪婪算法具有以下五个组成部分:
候选集 - 从该集合中创建解决方案。
选择函数 - 用于选择最佳候选者添加到解决方案中。
可行性函数 - 用于确定候选者是否可以用于贡献解决方案。
目标函数 - 用于为解决方案或部分解决方案赋值。
解决方案函数 - 用于指示是否已找到完整解决方案。
应用领域
贪婪方法用于解决许多问题,例如
使用 Dijkstra 算法查找两个顶点之间的最短路径。
使用 Prim/Kruskal 算法查找图中的最小生成树等。
贪婪方法失效之处
在许多问题中,贪婪算法都无法找到最优解,而且它可能会产生最差的解。旅行商问题和背包问题等问题无法使用这种方法解决。
硬币计数
这个问题是要通过选择尽可能少的硬币来计算到期望值,而贪婪方法迫使算法选择尽可能大的硬币。如果我们提供的是1、2、5和10卢比的硬币,并且我们被要求计算18卢比,那么贪婪程序将是:
选择一枚10卢比的硬币,剩余计数为8。
然后选择一枚5卢比的硬币,剩余计数为3。
然后选择一枚2卢比的硬币,剩余计数为1。
最后,选择一枚1卢比的硬币解决了这个问题。
尽管看起来工作正常,但对于此计数,我们只需要选择4枚硬币。但是,如果我们稍微改变一下问题,同样的方法可能无法产生相同的最佳结果。
对于我们拥有面值为1、7、10的硬币的货币系统,计算面值为18的硬币将是绝对最优的,但对于像15这样的计数,它可能使用的硬币比必要的要多。例如,贪婪方法将使用10 + 1 + 1 + 1 + 1 + 1,总共6枚硬币。而同样的问题可以用只有3枚硬币 (7 + 7 + 1) 来解决。
因此,我们可以得出结论,贪婪方法选择立即优化的解决方案,并且在全局优化是一个主要问题的地方可能会失败。
Java 数据结构 - 算法分析
算法是一个逐步的过程,它定义了一组指令,这些指令以一定的顺序执行以获得预期的输出。算法通常独立于底层语言创建,即一个算法可以在多种编程语言中实现。
算法分析
算法的效率可以在两个不同的阶段进行分析,即实现之前和实现之后。它们如下所示:
事前分析 − 这是对算法的理论分析。通过假设所有其他因素(例如处理器速度)都是恒定的并且对实现没有影响来衡量算法的效率。
事后分析 − 这是对算法的经验分析。所选算法使用编程语言实现。然后在目标计算机上执行。在此分析中,收集实际统计数据,例如运行时间和所需空间。
我们将学习事前算法分析。算法分析处理各种操作的执行或运行时间。操作的运行时间可以定义为每个操作执行的计算机指令数。
算法复杂度
假设X是一个算法,n是输入数据的大小,算法X使用的时空是决定X效率的两个主要因素。
时间因素 − 通过计算关键操作的数量(例如排序算法中的比较次数)来衡量时间。
空间因素 − 通过计算算法所需的最大内存空间来衡量空间。
算法的复杂度f(n)给出了算法的运行时间和/或存储空间,其中n表示输入数据的大小。
空间复杂度
算法的空间复杂度表示算法在其生命周期中所需的内存空间量。算法所需的空间等于以下两个部分的总和:
一个固定部分,这是存储某些数据和变量所需的空间,这些数据和变量与问题的规模无关。例如,使用的简单变量和常量、程序大小等。
一个可变部分,这是变量所需的空间,其大小取决于问题的规模。例如,动态内存分配、递归堆栈空间等。
任何算法P的空间复杂度S(P)为S(P) = C + SP(I),其中C是固定部分,S(I)是算法的可变部分,它取决于实例特征I。下面是一个简单的例子,试图解释这个概念:
算法:SUM(A, B)
Step 1: START Step 2: C <- A + B + 10 Step 3: Stop
这里我们有三个变量A、B和C以及一个常量。因此S(P) = 1 + 3。现在,空间取决于给定变量和常量类型的数据类型,并将相应地乘以。
时间复杂度
算法的时间复杂度表示算法运行到完成所需的时间量。时间需求可以定义为数值函数T(n),其中T(n)可以测量为步骤数,前提是每个步骤消耗恒定时间。
例如,两个n位整数的加法需要n个步骤。因此,总计算时间为T(n) = c * n,其中c是两个位相加所需的时间。在这里,我们观察到T(n)随着输入大小的增加而线性增长。
Java 数据结构 - 渐近符号
算法的渐近分析是指定义其运行时间性能的数学边界/框架。使用渐近分析,我们可以很好地得出算法的最坏情况、平均情况和最佳情况。
渐近分析是输入约束的,即如果算法没有输入,则认为它在恒定时间内工作。除“输入”外,所有其他因素都被认为是恒定的。
渐近分析是指用数学计算单元计算任何操作的运行时间。例如,一个操作的运行时间计算为f(n),另一个操作的运行时间计算为g(n2)。这意味着第一个操作的运行时间将随着n的增加而线性增加,而第二个操作的运行时间将随着n的增加而呈指数增长。同样,如果n非常小,则两个操作的运行时间几乎相同。
通常,算法所需的时间分为三种类型:
最佳情况 − 程序执行所需的最短时间。
平均情况 − 程序执行所需的平均时间。
最坏情况 − 程序执行所需的最长时间。
渐近符号
以下是常用的渐近符号,用于计算算法的运行时间复杂度。
Ο 符号
Ω 符号
θ 符号
大O符号,Ο
Ο(n)符号是表达算法运行时间上限的形式化方法。它衡量最坏情况下的时间复杂度,即算法可能完成所需的最长时间。
例如,对于函数f(n)
Ο(f(n)) = { g(n) : 存在c > 0和n0使得对于所有n > n0,f(n) ≤ c.g(n) 。}
欧米茄符号,Ω
Ω(n)符号是表达算法运行时间下限的形式化方法。它衡量最佳情况下的时间复杂度,即算法可能完成所需的最短时间。
例如,对于函数f(n)
Ω(f(n)) ≥ { g(n) : 存在c > 0和n0使得对于所有n > n0,g(n) ≤ c.f(n) 。}
西塔符号,θ
θ(n)符号是表达算法运行时间下限和上限的形式化方法。它表示如下:
θ(f(n)) = { g(n) 当且仅当 g(n) = Ο(f(n)) 且 g(n) = Ω(f(n)) 对于所有 n > n0 。}
常见的渐近符号
以下是一些常见的渐近符号的列表:
| 常数 | — | Ο(1) |
| 对数 | — | Ο(log n) |
| 线性 | — | Ο(n) |
| n log n | — | Ο(n log n) |
| 二次 | — | Ο(n2) |
| 三次 | — | Ο(n3) |
| 多项式 | — | nΟ(1) |
| 指数 | — | 2Ο(n) |
