树的中序遍历

在这种遍历方法中，先访问左子树，然后访问根节点，最后访问右子树。我们应该始终记住，每个节点都可以表示一个子树本身。

如果二叉树以中序方式遍历，则输出将生成按升序排序的键值。

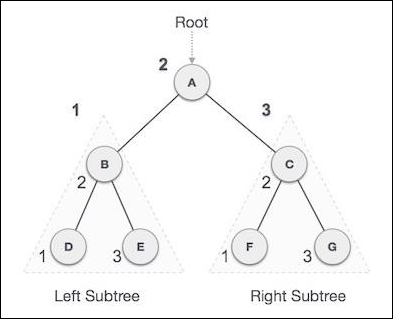
我们从A开始，按照中序遍历，移动到它的左子树B。B也以中序方式遍历。此过程持续进行，直到访问所有节点。这棵树的中序遍历的输出将为：

D → B → E → A → F → C → G

算法

直到所有节点都被遍历：

Step 1: Recursively traverse left subtree.
Step 2: Visit root node.
Step 3: Recursively traverse right subtree.

示例

class Node{
   int data;
   Node leftNode, rightNode;
   
   Node() {
      leftNode = null;
      rightNode = null;     
      this.data = data;
   }
   Node(int data) {
      leftNode = null;
      rightNode = null;     
      this.data = data;
   }
   int getData() {
      return this.data;	   
   }
   Node getleftNode() {
      return this.leftNode;      
   }
   Node getRightNode() {
      return this.leftNode;      
   }
   void setData(int data) {
      this.data = data; 
   }
   void setleftNode(Node leftNode) {
      this.leftNode = leftNode;      
   }
   void setRightNode(Node rightNode) {
      this.leftNode = rightNode;         
   }
}
public class InOrderBinaryTree {
   public static void main(String[] args) {
      Node node = new Node(50);
      node.leftNode = new Node(60);
      node.leftNode.leftNode = new Node(45);
      node.leftNode.rightNode = new Node(64);

      node.rightNode = new Node(60);
      node.rightNode.leftNode = new Node(45);
      node.rightNode.rightNode = new Node(64);
      System.out.println("inorder arrangement of given elements: ");
      inOrder(node);
   }
   public static void inOrder(Node root) {
      if(root !=null) {
         inOrder(root.leftNode);
         System.out.println(root.data);
         inOrder(root.rightNode);         
      }
   }
}

输出

inorder arrangement of given elements: 
45
60
64
50
45
60
64