最小生成树 (MST)

在加权图中，最小生成树是指权重小于同一图所有其他生成树的生成树。在现实情况下，此权重可以衡量为距离、拥塞、交通负荷或赋予边的任何任意值。

Java 中的 Prim 算法

Prim 算法（与克鲁斯卡尔算法一样）用于查找最小成本生成树，它使用贪心方法。Prim 算法与最短路径优先算法类似。

与克鲁斯卡尔算法相比，Prim 算法将节点视为一棵树，并不断从给定图中向生成树添加新节点。

为了与克鲁斯卡尔算法进行对比并更好地理解 Prim 算法，我们将使用相同的示例：

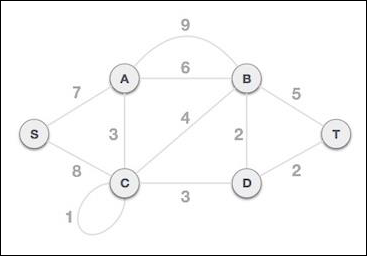
步骤 1 - 删除所有环和并行边

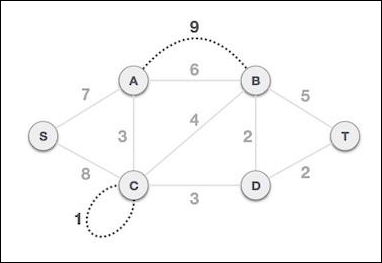
从给定图中删除所有环和并行边。如果存在并行边，则保留关联成本最低的边，并删除所有其他边。

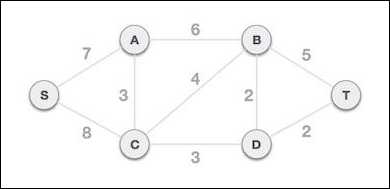
步骤 2 - 选择任意节点作为根节点

在本例中，我们选择S节点作为 Prim 生成树的根节点。此节点是任意选择的，因此任何节点都可以是根节点。有人可能会想知道为什么任何视频都可以是根节点。答案是，在生成树中，包含图的所有节点，并且由于它是连通的，因此必须至少有一条边将其连接到树的其余部分。

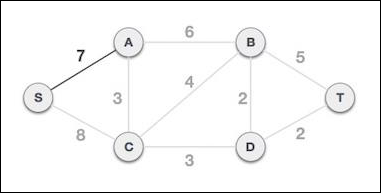
步骤 3 - 检查输出边并选择成本较低的边

选择根节点S后，我们看到 S，A 和 S，C 是两条权重分别为 7 和 8 的边。我们选择边 S，A，因为它小于另一条边。

现在，将树 S-7-A 视为一个节点，我们检查所有从中引出的边。我们选择成本最低的边并将其包含在树中。

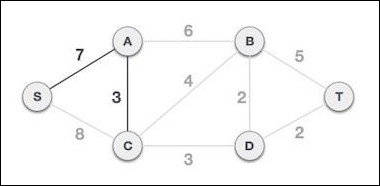
此步骤之后，将形成 S-7-A-3-C 树。现在，我们将再次将其视为一个节点，并再次检查所有边。但是，我们只会选择成本最低的边。在本例中，C-3-D 是新的边，它小于其他边的成本 8、6、4 等。

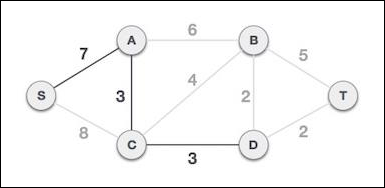
将节点D添加到生成树后，我们现在有两条从中引出的边具有相同的成本，即 D-2-T 和 D-2-B。因此，我们可以添加任意一个。但是下一步将再次产生边 2 作为最低成本。因此，我们显示了一个包含两条边的生成树。

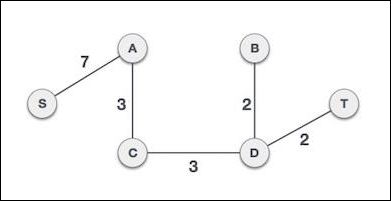
我们可能会发现，使用两种不同的算法对同一图得到的生成树是相同的。