Python程序：查找两城市之间捷径的距离

假设有n个城市，城市之间连接着两种类型的道路：高速公路和捷径。现在有一张地图，地图上只有高速公路，所有捷径都缺失。城市的交通部门希望推出一种交通工具，利用高速公路和捷径连接这些城市。当两个城市之间没有高速公路时，我们知道它们之间存在捷径。我们的任务是找到从起始城市到所有其他城市的捷径最小距离。

例如，输入如下：

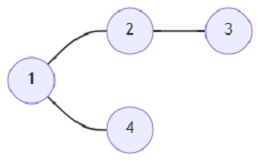
起始顶点(s)为1，则输出为3 1 2。

如果我们只走捷径，城市1和2之间的路径为1->3->4->2，成本为3。

同样地，

1和3：1->3，成本1。

1和4：1->3->4，成本2。

为了解决这个问题，我们将遵循以下步骤：

  • graph := 一个包含n个集合的新列表
  • 对于每对(x, y)在edges中，执行：
    • x := x - 1
    • y := y - 1
    • 将y插入graph[x]
    • 将x插入graph[y]
  • temp_arr := 一个包含值为-1的n大小的新数组
  • b_set := 一个包含键s - 1的新映射
  • f := 一个包含0到n的数字与b_set的差集的新集合
  • index := 0
  • 当b_set的大小>0时，执行：
    • 对于b_set中的每个元素a，执行：
      • temp_arr[a] := index
    • nxt := 一个包含graph中不是b_set子集的值的新映射
    • f := f与nxt的差集
    • b_set := nxt
    • index := index + 1
  • 返回temp_arr的非零值

示例

让我们看下面的实现来更好地理解：

def solve(n, edges, s):
    graph = [set() for i in range(n)]
    for (x, y) in edges:
        x -= 1
        y -= 1
        graph[x].add(y)
        graph[y].add(x)
    temp_arr = [-1] * n
    b_set = {s - 1}
    f = set(range(n)).difference(b_set)
    index = 0
    while len(b_set) > 0:
        for a in b_set:
            temp_arr[a] = index
        nxt = {f for f in f if not b_set.issubset(graph[f])}
        f = f.difference(nxt)
        b_set = nxt
        index += 1
    return (' '.join(str(t) for t in temp_arr if t > 0))    

print(solve(4, [(1, 2), (2, 3), (1, 4)], 1))

输入

4, [(1, 2), (2, 3), (1, 4)], 1

输出

3 1 2

更新于：2021年10月6日

412 次浏览

开启您的职业生涯

完成课程获得认证

开始学习
广告