
- Python 数据结构与算法教程
- Python - DS 首页
- Python - DS 简介
- Python - DS 环境
- Python - 数组
- Python - 列表
- Python - 元组
- Python - 字典
- Python - 二维数组
- Python - 矩阵
- Python - 集合
- Python - 映射
- Python - 链表
- Python - 栈
- Python - 队列
- Python - 双端队列
- Python - 高级链表
- Python - 哈希表
- Python - 二叉树
- Python - 搜索树
- Python - 堆
- Python - 图
- Python - 算法设计
- Python - 分治法
- Python - 递归
- Python - 回溯法
- Python - 排序算法
- Python - 搜索算法
- Python - 图算法
- Python - 算法分析
- Python - 大O表示法
- Python - 算法类别
- Python - 均摊分析
- Python - 算法论证
- Python 数据结构与算法实用资源
- Python - 快速指南
- Python - 实用资源
- Python - 讨论
Python 数据结构 - 快速指南
Python - DS 简介
在这里,我们将了解在 Python 编程语言中什么是数据结构。
数据结构概述
数据结构是计算机科学的基本概念,有助于用任何语言编写高效的程序。Python 是一种高级的、解释型的、交互式的和面向对象的脚本语言,使用它我们可以比其他编程语言更简单地学习数据结构的基础知识。
在本章中,我们将简要概述一些常用的通用数据结构,以及它们与某些特定的 Python 数据类型之间的关系。还有一些特定于 Python 的数据结构,它们被列为另一类。
通用数据结构
计算机科学中的各种数据结构大致分为以下两类。我们将在后续章节中详细讨论每种数据结构。
线性数据结构
这些是按顺序存储数据元素的数据结构。
数组 - 它是由数据元素及其索引配对组成的顺序排列。
链表 - 每个数据元素除了包含数据外,还包含指向另一个元素的链接。
栈 - 它是一种只遵循特定操作顺序的数据结构。后进先出 (LIFO) 或先进后出 (FILO)。
队列 - 它类似于栈,但操作顺序仅为先进先出 (FIFO)。
矩阵 - 它是一种二维数据结构,其中数据元素由一对索引引用。
非线性数据结构
这些是数据元素之间没有顺序链接的数据结构。任何一对或一组数据元素都可以相互链接,并且可以无需严格的顺序访问。
二叉树 - 它是一种数据结构,其中每个数据元素最多可以连接到另外两个数据元素,并且它以根节点开始。
堆 - 它是树数据结构的一种特殊情况,其中父节点中的数据要么严格大于/等于子节点,要么严格小于子节点。
哈希表 - 它是由使用哈希函数相互关联的数组组成的数据结构。它使用键而不是数据元素的索引来检索值。
图 - 它是由顶点和节点组成的排列,其中某些节点通过链接相互连接。
Python 特定数据结构
这些数据结构特定于 Python 语言,它们在存储不同类型的数据和在 Python 环境中进行更快的处理方面提供了更大的灵活性。
列表 - 它类似于数组,但数据元素可以是不同数据类型。您可以在 Python 列表中同时拥有数字和字符串数据。
元组 - 元组类似于列表,但它们是不可变的,这意味着元组中的值不能修改,只能读取。
字典 - 字典包含键值对作为其数据元素。
在接下来的章节中,我们将学习如何使用 Python 实现每个数据结构的详细信息。
Python - DS 环境
Python 可用于各种平台,包括 Linux 和 Mac OS X。让我们了解如何设置我们的 Python 环境。
本地环境设置
打开一个终端窗口,然后键入“python”以查看它是否已安装以及安装了哪个版本。
- Unix(Solaris、Linux、FreeBSD、AIX、HP/UX、SunOS、IRIX 等)
- Win 9x/NT/2000
- Macintosh(Intel、PPC、68K)
- OS/2
- DOS(多个版本)
- PalmOS
- 诺基亚手机
- Windows CE
- Acorn/RISC OS
- BeOS
- Amiga
- VMS/OpenVMS
- QNX
- VxWorks
- Psion
- Python 也已移植到 Java 和 .NET 虚拟机
获取 Python
最新的源代码、二进制文件、文档、新闻等都可以在 Python 的官方网站上找到 www.python.org
您可以从此处提供的网站下载 Python 文档,www.python.org/doc。该文档以 HTML、PDF 和 PostScript 格式提供。
安装 Python
Python 发行版适用于各种平台。您只需要下载适用于您平台的二进制代码并安装 Python。
如果您的平台没有提供二进制代码,则需要一个 C 编译器来手动编译源代码。编译源代码在您所需的安装功能方面提供了更大的灵活性。
以下是关于在各种平台上安装 Python 的快速概述 -
Unix 和 Linux 安装
以下是在 Unix/Linux 机器上安装 Python 的简单步骤。
打开 Web 浏览器并转到 www.python.org/downloads。
点击链接下载适用于 Unix/Linux 的压缩源代码。
下载并解压缩文件。
如果您想自定义某些选项,请编辑Modules/Setup 文件。
运行 ./configure 脚本
make
make install
这会将 Python 安装到标准位置/usr/local/bin,并将库安装到/usr/local/lib/pythonXX,其中 XX 是 Python 的版本。
Windows 安装
以下是在 Windows 机器上安装 Python 的步骤。
打开 Web 浏览器并转到 www.python.org/downloads。
点击 Windows 安装程序python-XYZ.msi 文件的链接,其中 XYZ 是您需要安装的版本。
要使用此安装程序python-XYZ.msi,Windows 系统必须支持 Microsoft Installer 2.0。将安装程序文件保存到您的本地机器,然后运行它以查看您的机器是否支持 MSI。
运行下载的文件。这将打开 Python 安装向导,该向导非常易于使用。只需接受默认设置,等待安装完成,即可完成。
Macintosh 安装
最近的 Mac 都已安装了 Python,但它可能已经过时几年了。请参阅 www.python.org/download/mac/,了解有关获取最新版本以及支持在 Mac 上进行开发的其他工具的说明。对于 Mac OS X 10.3(2003 年发布)之前的旧版 Mac OS,可以使用 MacPython。
Jack Jansen 维护它,您可以在他的网站上完全访问所有文档 - http://www.cwi.nl/~jack/macpython.html。您可以在其中找到 Mac OS 安装的完整安装详细信息。
设置 PATH
程序和其他可执行文件可能位于许多目录中,因此操作系统提供了一个搜索路径,该路径列出了操作系统搜索可执行文件的目录。
该路径存储在环境变量中,环境变量是操作系统维护的命名字符串。此变量包含命令 shell 和其他程序可用的信息。
路径变量在 Unix 中命名为 PATH,在 Windows 中命名为 Path(Unix 区分大小写;Windows 不区分)。
在 Mac OS 中,安装程序会处理路径详细信息。要从任何特定目录调用 Python 解释器,您必须将 Python 目录添加到您的路径中。
在 Unix/Linux 上设置路径
要在 Unix 中为特定会话将 Python 目录添加到路径中 -
在 csh shell 中 - 键入 setenv PATH "$PATH:/usr/local/bin/python" 并按 Enter。
在 bash shell(Linux)中 - 键入 export ATH="$PATH:/usr/local/bin/python" 并按 Enter。
在 sh 或 ksh shell 中 - 键入 PATH="$PATH:/usr/local/bin/python" 并按 Enter。
注意 - /usr/local/bin/python 是 Python 目录的路径
在 Windows 上设置路径
要在 Windows 中为特定会话将 Python 目录添加到路径中 -
在命令提示符下 - 键入 path %path%;C:\Python 并按 Enter。
注意 - C:\Python 是 Python 目录的路径
Python 环境变量
以下是 Python 可以识别的重要环境变量 -
| 序号 | 变量和描述 |
|---|---|
| 1 |
PYTHONPATH 它与 PATH 的作用类似。此变量告诉 Python 解释器在哪里查找导入到程序中的模块文件。它应包含 Python 源库目录和包含 Python 源代码的目录。PYTHONPATH 有时由 Python 安装程序预设。 |
| 2 |
PYTHONSTARTUP 它包含一个初始化文件的路径,该文件包含 Python 源代码。每次启动解释器时都会执行它。在 Unix 中它被命名为.pythonrc.py,并且包含加载实用程序或修改 PYTHONPATH 的命令。 |
| 3 |
PYTHONCASEOK 它用于 Windows,指示 Python 在 import 语句中查找第一个不区分大小写的匹配项。将此变量设置为任何值以激活它。 |
| 4 |
PYTHONHOME 它是一个备用的模块搜索路径。它通常嵌入在 PYTHONSTARTUP 或 PYTHONPATH 目录中,以便轻松切换模块库。 |
运行 Python
有三种不同的方法可以启动 Python,如下所示:
交互式解释器
您可以从 Unix、DOS 或任何其他提供命令行解释器或 shell 窗口的系统启动 Python。
在命令行中输入python。
立即在交互式解释器中开始编码。
$python # Unix/Linux or python% # Unix/Linux or C:> python # Windows/DOS
以下是所有可用命令行选项的列表,如下所示:
| 序号 | 选项 & 说明 |
|---|---|
| 1 |
-d 它提供调试输出。 |
| 2 |
-O 它生成优化的字节码(生成 .pyo 文件)。 |
| 3 |
-S 在启动时不要运行 import site 来查找 Python 路径。 |
| 4 |
-v 详细输出(import 语句的详细跟踪)。 |
| 5 |
-X 禁用基于类的内置异常(只使用字符串);从版本 1.6 开始已过时。 |
| 6 |
-c cmd 运行作为 cmd 字符串发送的 Python 脚本 |
| 7 |
file 从给定文件运行 Python 脚本 |
来自命令行的脚本
可以通过在您的应用程序上调用解释器来在命令行中执行 Python 脚本,如下所示:
$python script.py # Unix/Linux or python% script.py # Unix/Linux or C: >python script.py # Windows/DOS
注意 - 请确保文件权限模式允许执行。
集成开发环境(IDE)
如果您系统上有一个支持 Python 的 GUI 应用程序,您也可以从图形用户界面 (GUI) 环境运行 Python。
Unix - IDLE 是第一个用于 Python 的 Unix IDE。
Windows - PythonWin 是第一个用于 Python 的 Windows 接口,并且是一个带有 GUI 的 IDE。
Macintosh - Macintosh 版本的 Python 以及 IDLE IDE 可从主网站获得,可以下载为 MacBinary 或 BinHex'd 文件。
如果您无法正确设置环境,则可以向系统管理员寻求帮助。确保 Python 环境已正确设置并正常工作。
注意 - 后续章节中给出的所有示例均使用 CentOS 版本的 Linux 上可用的 Python 2.4.3 版本执行。
我们已经在网上设置了 Python 编程环境,以便您可以在学习理论的同时在线执行所有可用示例。随意修改任何示例并在网上执行它。
Python - 数组
数组是一个容器,它可以容纳固定数量的项,并且这些项的类型必须相同。大多数数据结构都使用数组来实现其算法。以下是理解数组概念的重要术语:
元素 - 存储在数组中的每个项目称为元素。
索引 - 数组中每个元素的位置都有一个数字索引,用于识别该元素。
数组表示
可以在不同语言中以各种方式声明数组。下面是一个示例。


根据上图,以下是要考虑的重要事项:
索引从 0 开始。
数组长度为 10,这意味着它可以存储 10 个元素。
每个元素都可以通过其索引访问。例如,我们可以获取索引为 6 的元素,即 9。
基本操作
数组支持的基本操作如下所示:
遍历 - 一次打印所有数组元素。
插入 - 在给定索引处添加一个元素。
删除 - 删除给定索引处的元素。
搜索 - 使用给定索引或值搜索元素。
更新 - 更新给定索引处的元素。
在 Python 中,通过将 array 模块导入到 Python 程序中来创建数组。然后,声明数组如下所示:
from array import * arrayName = array(typecode, [Initializers])
Typecode 是用于定义数组将保存的值类型的代码。一些常用的 typecode 如下所示:
| Typecode | 值 |
|---|---|
| b | 表示大小为 1 字节的有符号整数 |
| B | 表示大小为 1 字节的无符号整数 |
| c | 表示大小为 1 字节的字符 |
| i | 表示大小为 2 字节的有符号整数 |
| I | 表示大小为 2 字节的无符号整数 |
| f | 表示大小为 4 字节的浮点数 |
| d | 表示大小为 8 字节的浮点数 |
在查看各种数组操作之前,让我们使用 python 创建并打印一个数组。
示例
以下代码创建了一个名为array1的数组。
from array import *
array1 = array('i', [10,20,30,40,50])
for x in array1:
print(x)
输出
当我们编译并执行上述程序时,它会产生以下结果:
10 20 30 40 50
访问数组元素
我们可以使用元素的索引访问数组的每个元素。以下代码显示了如何访问数组元素。
示例
from array import *
array1 = array('i', [10,20,30,40,50])
print (array1[0])
print (array1[2])
输出
当我们编译并执行上述程序时,它会产生以下结果,该结果显示元素已插入索引位置 1。
10 30
插入操作
插入操作是指将一个或多个数据元素插入数组。根据需求,可以在数组的开头、结尾或任何给定索引处添加新元素。
示例
在这里,我们使用 python 内置的 insert() 方法在数组中间添加一个数据元素。
from array import *
array1 = array('i', [10,20,30,40,50])
array1.insert(1,60)
for x in array1:
print(x)
当我们编译并执行上述程序时,它会产生以下结果,该结果显示元素已插入索引位置 1。
输出
10 60 20 30 40 50
删除操作
删除是指从数组中删除现有元素并重新组织数组的所有元素。
示例
在这里,我们使用 python 内置的 remove() 方法删除数组中间的数据元素。
from array import *
array1 = array('i', [10,20,30,40,50])
array1.remove(40)
for x in array1:
print(x)
输出
当我们编译并执行上述程序时,它会产生以下结果,该结果显示元素已从数组中删除。
10 20 30 50
搜索操作
您可以根据元素的值或索引执行数组元素的搜索。
示例
在这里,我们使用 python 内置的 index() 方法搜索数据元素。
from array import *
array1 = array('i', [10,20,30,40,50])
print (array1.index(40))
输出
当我们编译并执行上述程序时,它会产生以下结果,该结果显示元素的索引。如果数组中不存在该值,则程序会返回错误。
3
更新操作
更新操作是指更新给定索引处数组中的现有元素。
示例
在这里,我们只需将新值重新分配到我们要更新的所需索引。
from array import *
array1 = array('i', [10,20,30,40,50])
array1[2] = 80
for x in array1:
print(x)
输出
当我们编译并执行上述程序时,它会产生以下结果,该结果显示索引位置 2 的新值。
10 20 80 40 50
Python - 列表
列表是 Python 中最通用的数据类型,可以写成方括号之间用逗号分隔的值(项)的列表。关于列表的重要一点是,列表中的项不必是相同类型。
创建列表就像在方括号之间放置不同的逗号分隔的值一样简单。
例如
list1 = ['physics', 'chemistry', 1997, 2000] list2 = [1, 2, 3, 4, 5 ] list3 = ["a", "b", "c", "d"]
类似于字符串索引,列表索引从 0 开始,并且可以对列表进行切片、连接等等。
访问值
要访问列表中的值,请使用方括号进行切片,并使用索引或索引来获取该索引处的值。
例如
#!/usr/bin/python
list1 = ['physics', 'chemistry', 1997, 2000]
list2 = [1, 2, 3, 4, 5, 6, 7 ]
print ("list1[0]: ", list1[0])
print ("list2[1:5]: ", list2[1:5])
当执行上述代码时,它会产生以下结果:
list1[0]: physics list2[1:5]: [2, 3, 4, 5]
更新列表
您可以通过在赋值运算符左侧进行切片来更新列表的单个或多个元素,并且可以使用 append() 方法向列表中添加元素。
例如
#!/usr/bin/python
list = ['physics', 'chemistry', 1997, 2000]
print ("Value available at index 2 : ")
print (list[2])
list[2] = 2001
print ("New value available at index 2 : ")
print (list[2])
注意 - append() 方法将在后续部分中讨论。
当执行上述代码时,它会产生以下结果:
Value available at index 2 : 1997 New value available at index 2 : 2001
删除列表元素
要删除列表元素,如果确切知道要删除哪个元素,则可以使用 del 语句;如果不知道,则可以使用 remove() 方法。
例如
#!/usr/bin/python
list1 = ['physics', 'chemistry', 1997, 2000]
print (list1)
del list1[2]
print ("After deleting value at index 2 : ")
print (list1)
当执行上述代码时,它会产生以下结果:
['physics', 'chemistry', 1997, 2000] After deleting value at index 2 : ['physics', 'chemistry', 2000]
注意 - remove() 方法将在后续部分中讨论。
基本列表操作
列表对 + 和 * 运算符的响应与字符串非常相似;它们在这里也表示连接和重复,只是结果是一个新列表,而不是字符串。
事实上,列表对我们在上一章中对字符串使用过的所有通用序列操作都有响应。
| Python 表达式 | 结果 | 描述 |
|---|---|---|
| len([1, 2, 3]) | 3 | 长度 |
| [1, 2, 3] + [4, 5, 6] | [1, 2, 3, 4, 5, 6] | 连接 |
| ['Hi!'] * 4 | ['Hi!', 'Hi!', 'Hi!', 'Hi!'] | 重复 |
| 3 in [1, 2, 3] | True | 成员资格 |
| for x in [1, 2, 3]: print x, | 1 2 3 | 迭代 |
Python - 元组
元组是不可变的 Python 对象的序列。元组是序列,就像列表一样。元组和列表之间的区别在于,元组不能像列表那样更改,并且元组使用括号,而列表使用方括号。
创建元组就像放置不同的逗号分隔的值一样简单。可以选择将这些逗号分隔的值放在括号之间。
例如
tup1 = ('physics', 'chemistry', 1997, 2000);
tup2 = (1, 2, 3, 4, 5 );
tup3 = "a", "b", "c", "d";
空元组写成两个不包含任何内容的括号 - {}。
tup1 = ();
要编写包含单个值的元组,您必须包含逗号,即使只有一个值 - {}。
tup1 = (50,);
类似于字符串索引,元组索引从 0 开始,并且可以对它们进行切片、连接等等。
访问元组中的值
要访问元组中的值,请使用方括号进行切片,并使用索引或索引来获取该索引处的值。
例如
#!/usr/bin/python
tup1 = ('physics', 'chemistry', 1997, 2000);
tup2 = (1, 2, 3, 4, 5, 6, 7 );
print ("tup1[0]: ", tup1[0])
print ("tup2[1:5]: ", tup2[1:5])
当执行上述代码时,它会产生以下结果:
tup1[0]: physics tup2[1:5]: [2, 3, 4, 5]
更新元组
元组是不可变的,这意味着您不能更新或更改元组元素的值。您可以使用现有元组的部分来创建新的元组,如下面的示例所示:
#!/usr/bin/python
tup1 = (12, 34.56);
tup2 = ('abc', 'xyz');
# Following action is not valid for tuples
# tup1[0] = 100;
# So let's create a new tuple as follows
tup3 = tup1 + tup2;
print (tup3);
当执行上述代码时,它会产生以下结果:
(12, 34.56, 'abc', 'xyz')
删除元组元素
无法删除单个元组元素。当然,将另一个元组放在一起并丢弃不需要的元素没有任何问题。
要显式删除整个元组,只需使用del语句即可。
例如
#!/usr/bin/python
tup = ('physics', 'chemistry', 1997, 2000);
print (tup);
del tup;
print ("After deleting tup : ");
print (tup);
注意 - 抛出异常,这是因为在del tup之后,元组不再存在。
这会产生以下结果:
('physics', 'chemistry', 1997, 2000)
After deleting tup :
Traceback (most recent call last):
File "test.py", line 9, in <module>
print tup;
NameError: name 'tup' is not defined
基本元组操作
元组对 + 和 * 运算符的响应与字符串非常相似;它们在这里也表示连接和重复,只是结果是一个新的元组,而不是字符串。
事实上,元组对我们在上一章中对字符串使用过的所有通用序列操作都有响应。
| Python 表达式 | 结果 | 描述 |
|---|---|---|
| len((1, 2, 3)) | 3 | 长度 |
| (1, 2, 3) + (4, 5, 6) | (1, 2, 3, 4, 5, 6) | 连接 |
| ('Hi!',) * 4 | ('Hi!', 'Hi!', 'Hi!', 'Hi!') | 重复 |
| 3 in (1, 2, 3) | True | 成员资格 |
| for x in (1, 2, 3): print x, | 1 2 3 | 迭代 |
Python - 字典
在字典中,每个键与其值之间用冒号 (:) 分隔,项用逗号分隔,整个内容用花括号括起来。一个没有任何项的空字典只写成两个花括号,如下所示 - {}。
键在字典中是唯一的,而值则不一定唯一。字典的值可以是任何类型,但键必须是不可变的数据类型,例如字符串、数字或元组。
访问字典中的值
要访问字典元素,您可以使用熟悉的方括号以及键来获取其值。
示例
一个简单的示例如下所示:
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
print ("dict['Name']: ", dict['Name'])
print ("dict['Age']: ", dict['Age'])
输出
当执行上述代码时,它会产生以下结果:
dict['Name']: Zara dict['Age']: 7
如果我们尝试访问字典中不存在的键对应的值,则会得到如下错误:
示例
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
print ("dict['Alice']: ", dict['Alice'])
输出
当执行上述代码时,它会产生以下结果:
dict['Alice']:
Traceback (most recent call last):
File "test.py", line 4, in <module>
print "dict['Alice']: ", dict['Alice'];
KeyError: 'Alice'
更新字典
您可以通过添加新条目或键值对、修改现有条目或删除现有条目来更新字典,如下面的简单示例所示:
示例
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
dict['Age'] = 8; # update existing entry
dict['School'] = "DPS School"; # Add new entry
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
输出
当执行上述代码时,它会产生以下结果:
dict['Age']: 8 dict['School']: DPS School
删除字典元素
您可以删除单个字典元素或清除字典的全部内容。您也可以通过单个操作删除整个字典。
示例
要显式删除整个字典,只需使用 **del** 语句。一个简单的示例如下所示:
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
del dict['Name']; # remove entry with key 'Name'
dict.clear(); # remove all entries in dict
del dict ; # delete entire dictionary
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
**注意** - 因为在 **del dict** 之后,字典就不再存在了,所以会引发异常。
输出
这会产生以下结果:
dict['Age']: dict['Age'] dict['School']: dict['School']
**注意** - del() 方法将在后续章节中讨论。
字典键的属性
字典值没有任何限制。它们可以是任何任意的 Python 对象,无论是标准对象还是用户定义的对象。但是,键则不是这样。
关于字典键,有两点需要注意:
每个键只能有一个条目。这意味着不允许重复键。当在赋值期间遇到重复键时,最后一次赋值会生效。
例如
#!/usr/bin/python
dict = {'Name': 'Zara', 'Age': 7, 'Name': 'Manni'}
print ("dict['Name']: ", dict['Name'])
输出
当执行上述代码时,它会产生以下结果:
dict['Name']: Manni
键必须是不可变的。这意味着您可以使用字符串、数字或元组作为字典键,但诸如 ['key'] 之类的东西是不允许的。
示例
一个例子如下:
#!/usr/bin/python
dict = {['Name']: 'Zara', 'Age': 7}
print ("dict['Name']: ", dict['Name'])
输出
当执行上述代码时,它会产生以下结果:
Traceback (most recent call last):
File "test.py", line 3, in <module>
dict = {['Name']: 'Zara', 'Age': 7};
TypeError: list objects are unhashable
Python - 二维数组
二维数组是在数组内的数组。它是一个数组的数组。在这种类型的数组中,数据元素的位置由两个索引而不是一个索引来引用。因此,它表示一个包含数据行和列的表格。
在下面的二维数组示例中,观察到每个数组元素本身也是一个数组。
考虑每天记录 4 次温度的例子。有时记录仪器可能出现故障,导致我们无法记录数据。4 天的此类数据可以表示为如下所示的二维数组。
Day 1 - 11 12 5 2 Day 2 - 15 6 10 Day 3 - 10 8 12 5 Day 4 - 12 15 8 6
上述数据可以用如下所示的二维数组表示。
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
访问值
二维数组中的数据元素可以使用两个索引访问。一个索引引用主数组或父数组,另一个索引引用数据元素在内部数组中的位置。如果我们只提及一个索引,则会打印该索引位置的整个内部数组。
示例
下面的示例说明了它是如何工作的。
from array import * T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]] print(T[0]) print(T[1][2])
输出
当执行上述代码时,它会产生以下结果:
[11, 12, 5, 2] 10
要打印出整个二维数组,我们可以使用 python for 循环,如下所示。我们使用换行符在不同的行中打印出值。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
for r in T:
for c in r:
print(c,end = " ")
print()
输出
当执行上述代码时,它会产生以下结果:
11 12 5 2 15 6 10 10 8 12 5 12 15 8 6
插入值
我们可以使用 insert() 方法并指定索引,在特定位置插入新的数据元素。
示例
在下面的示例中,一个新的数据元素插入到索引位置 2。
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T.insert(2, [0,5,11,13,6])
for r in T:
for c in r:
print(c,end = " ")
print()
输出
当执行上述代码时,它会产生以下结果:
11 12 5 2 15 6 10 0 5 11 13 6 10 8 12 5 12 15 8 6
更新值
我们可以通过使用数组索引重新赋值来更新整个内部数组或内部数组的一些特定数据元素。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
T[2] = [11,9]
T[0][3] = 7
for r in T:
for c in r:
print(c,end = " ")
print()
输出
当执行上述代码时,它会产生以下结果:
11 12 5 7 15 6 10 11 9 12 15 8 6
删除值
我们可以通过使用带索引的 del() 方法重新赋值来删除整个内部数组或内部数组的一些特定数据元素。但是,如果您需要删除其中一个内部数组中的特定数据元素,则使用上面描述的更新过程。
示例
from array import *
T = [[11, 12, 5, 2], [15, 6,10], [10, 8, 12, 5], [12,15,8,6]]
del T[3]
for r in T:
for c in r:
print(c,end = " ")
print()
输出
当执行上述代码时,它会产生以下结果:
11 12 5 2 15 6 10 10 8 12 5
Python - 矩阵
矩阵是二维数组的一种特殊情况,其中每个数据元素的大小都严格相同。因此,每个矩阵也是一个二维数组,反之则不然。
矩阵对于许多数学和科学计算来说是非常重要的数据结构。由于我们已经在上一章中讨论了二维数组数据结构,因此本章将重点介绍特定于矩阵的数据结构操作。
我们还将使用 numpy 包进行矩阵数据操作。
矩阵示例
考虑记录一周温度的案例,在早上、中午、晚上和午夜测量。它可以使用数组和 numpy 中可用的 reshape 方法表示为 7X5 矩阵。
from numpy import * a = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = reshape(a,(7,5)) print(m)
输出
上述数据可以用如下所示的二维数组表示:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
访问值
矩阵中的数据元素可以通过使用索引来访问。访问方法与在二维数组中访问数据的方式相同。
示例
from numpy import *
m = array([['Mon',18,20,22,17],['Tue',11,18,21,18],
['Wed',15,21,20,19],['Thu',11,20,22,21],
['Fri',18,17,23,22],['Sat',12,22,20,18],
['Sun',13,15,19,16]])
# Print data for Wednesday
print(m[2])
# Print data for friday evening
print(m[4][3])
输出
当执行上述代码时,它会产生以下结果:
['Wed', 15, 21, 20, 19] 23
添加一行
使用下面提到的代码在矩阵中添加一行。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m_r = append(m,[['Avg',12,15,13,11]],0) print(m_r)
输出
当执行上述代码时,它会产生以下结果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ['Avg' '12' '15' '13' '11'] ]
添加一列
我们可以使用 insert() 方法向矩阵添加列。在这里,我们必须提及要添加列的索引以及包含添加列的新值的数组。在下面的示例中,我们在从开头算起的第五个位置添加了一列。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m_c = insert(m,[5],[[1],[2],[3],[4],[5],[6],[7]],1) print(m_c)
输出
当执行上述代码时,它会产生以下结果:
[ ['Mon' '18' '20' '22' '17' '1'] ['Tue' '11' '18' '21' '18' '2'] ['Wed' '15' '21' '20' '19' '3'] ['Thu' '11' '20' '22' '21' '4'] ['Fri' '18' '17' '23' '22' '5'] ['Sat' '12' '22' '20' '18' '6'] ['Sun' '13' '15' '19' '16' '7'] ]
删除一行
我们可以使用 delete() 方法从矩阵中删除一行。我们必须指定行的索引以及轴值,对于行,轴值为 0,对于列,轴值为 1。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = delete(m,[2],0) print(m)
输出
当执行上述代码时,它会产生以下结果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Thu' '11' '20' '22' '21'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
删除一列
我们可以使用 delete() 方法从矩阵中删除一列。我们必须指定列的索引以及轴值,对于行,轴值为 0,对于列,轴值为 1。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m = delete(m,s_[2],1) print(m)
输出
当执行上述代码时,它会产生以下结果:
[ ['Mon' '18' '22' '17'] ['Tue' '11' '21' '18'] ['Wed' '15' '20' '19'] ['Thu' '11' '22' '21'] ['Fri' '18' '23' '22'] ['Sat' '12' '20' '18'] ['Sun' '13' '19' '16'] ]
更新一行
要更新矩阵中行的值,我们只需重新分配行索引处的值。在下面的示例中,星期四的所有数据都标记为零。此行的索引为 3。
示例
from numpy import * m = array([['Mon',18,20,22,17],['Tue',11,18,21,18], ['Wed',15,21,20,19],['Thu',11,20,22,21], ['Fri',18,17,23,22],['Sat',12,22,20,18], ['Sun',13,15,19,16]]) m[3] = ['Thu',0,0,0,0] print(m)
输出
当执行上述代码时,它会产生以下结果:
[ ['Mon' '18' '20' '22' '17'] ['Tue' '11' '18' '21' '18'] ['Wed' '15' '21' '20' '19'] ['Thu' '0' '0' '0' '0'] ['Fri' '18' '17' '23' '22'] ['Sat' '12' '22' '20' '18'] ['Sun' '13' '15' '19' '16'] ]
Python - 集合
在数学上,集合是一组项目,没有特定的顺序。Python 集合类似于此数学定义,并具有以下附加条件。
集合中的元素不能重复。
集合中的元素是不可变的(不能修改),但集合作为一个整体是可变的。
Python 集合中的任何元素都没有附加索引。因此,它们不支持任何索引或切片操作。
集合操作
Python 中的集合通常用于数学运算,如并集、交集、差集和补集等。我们可以创建一个集合,访问其元素并执行这些数学运算,如下所示。
创建集合
集合是通过使用 set() 函数或将所有元素放在一对花括号内来创建的。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
Months={"Jan","Feb","Mar"}
Dates={21,22,17}
print(Days)
print(Months)
print(Dates)
输出
执行上述代码时,会产生以下结果。请注意结果中元素的顺序是如何改变的。
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat']) set(['Jan', 'Mar', 'Feb']) set([17, 21, 22])
我们无法访问集合中的单个值。我们只能像上面那样一起访问所有元素。但是我们也可以通过循环遍历集合来获取单个元素的列表。
访问集合中的值
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"]) for d in Days: print(d)
输出
当执行上述代码时,它会产生以下结果:
Wed Sun Fri Tue Mon Thu Sat
向集合中添加项目
我们可以使用 add() 方法向集合中添加元素。同样,正如我们所讨论的,新添加的元素没有附加特定的索引。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat"])
Days.add("Sun")
print(Days)
输出
当执行上述代码时,它会产生以下结果:
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
从集合中删除项目
我们可以使用 discard() 方法从集合中删除元素。同样,正如我们所讨论的,新添加的元素没有附加特定的索引。
示例
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat"])
Days.discard("Sun")
print(Days)
输出
执行上述代码时,会产生以下结果。
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
集合的并集
两个集合的并集操作会生成一个新的集合,其中包含两个集合中所有不同的元素。在下面的示例中,元素“Wed”同时存在于两个集合中。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA|DaysB print(AllDays)
输出
执行上述代码时,会产生以下结果。请注意,结果中只有一个“wed”。
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
集合的交集
两个集合的交集操作会生成一个新的集合,其中仅包含两个集合中共同的元素。在下面的示例中,元素“Wed”同时存在于两个集合中。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA & DaysB print(AllDays)
输出
执行上述代码时,会产生以下结果。请注意,结果中只有一个“wed”。
set(['Wed'])
集合的差集
两个集合的差集操作会生成一个新的集合,其中仅包含第一个集合中的元素,而不包含第二个集合中的元素。在下面的示例中,元素“Wed”同时存在于两个集合中,因此在结果集中将找不到它。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Wed","Thu","Fri","Sat","Sun"]) AllDays = DaysA - DaysB print(AllDays)
输出
执行上述代码时,会产生以下结果。请注意,结果中只有一个“wed”。
set(['Mon', 'Tue'])
比较集合
我们可以检查给定的集合是否是另一个集合的子集或超集。结果为 True 或 False,具体取决于集合中存在的元素。
示例
DaysA = set(["Mon","Tue","Wed"]) DaysB = set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"]) SubsetRes = DaysA <= DaysB SupersetRes = DaysB >= DaysA print(SubsetRes) print(SupersetRes)
输出
当执行上述代码时,它会产生以下结果:
True True
Python - 映射
Python 映射,也称为 ChainMap,是一种数据结构,用于将多个字典作为一个单元一起管理。组合字典包含以特定顺序排列的键值对,消除了任何重复的键。ChainMap 的最佳用途是同时搜索多个字典并获得正确的键值对映射。我们还看到这些 ChainMap 具有栈数据结构的行为。
创建 ChainMap
我们创建两个字典,并使用 collections 库中的 ChainMap 方法将它们组合在一起。然后,我们打印组合字典结果的键和值。如果存在重复键,则仅保留第一个键的值。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day1': 'Thu'}
res = collections.ChainMap(dict1, dict2)
# Creating a single dictionary
print(res.maps,'\n')
print('Keys = {}'.format(list(res.keys())))
print('Values = {}'.format(list(res.values())))
print()
# Print all the elements from the result
print('elements:')
for key, val in res.items():
print('{} = {}'.format(key, val))
print()
# Find a specific value in the result
print('day3 in res: {}'.format(('day1' in res)))
print('day4 in res: {}'.format(('day4' in res)))
输出
当执行上述代码时,它会产生以下结果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day1': 'Thu', 'day3': 'Wed'}]
Keys = ['day1', 'day3', 'day2']
Values = ['Mon', 'Wed', 'Tue']
elements:
day1 = Mon
day3 = Wed
day2 = Tue
day3 in res: True
day4 in res: False
映射重新排序
如果我们在上面的示例中更改字典的组合顺序,我们会看到元素的位置会互换,就像它们在一个连续的链中一样。这再次表明映射作为栈的行为。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day4': 'Thu'}
res1 = collections.ChainMap(dict1, dict2)
print(res1.maps,'\n')
res2 = collections.ChainMap(dict2, dict1)
print(res2.maps,'\n')
输出
当执行上述代码时,它会产生以下结果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Thu'}]
[{'day3': 'Wed', 'day4': 'Thu'}, {'day1': 'Mon', 'day2': 'Tue'}]
更新映射
当字典的元素更新时,结果会立即更新到 ChainMap 的结果中。在下面的示例中,我们看到新的更新值反映在结果中,而无需再次显式应用 ChainMap 方法。
示例
import collections
dict1 = {'day1': 'Mon', 'day2': 'Tue'}
dict2 = {'day3': 'Wed', 'day4': 'Thu'}
res = collections.ChainMap(dict1, dict2)
print(res.maps,'\n')
dict2['day4'] = 'Fri'
print(res.maps,'\n')
输出
当执行上述代码时,它会产生以下结果:
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Thu'}]
[{'day1': 'Mon', 'day2': 'Tue'}, {'day3': 'Wed', 'day4': 'Fri'}]
Python - 链表
链表是一系列数据元素,它们通过链接连接在一起。每个数据元素都包含一个指向另一个数据元素的指针。Python 的标准库中没有链表。我们使用节点的概念来实现链表的概念,如上一章所述。
我们已经了解了如何创建节点类以及如何遍历节点的元素。在本章中,我们将研究称为单链表的链表类型。在这种数据结构中,任意两个数据元素之间只有一个链接。我们创建这样的列表,并创建其他方法来插入、更新和删除列表中的元素。
链表的创建
链表是使用上一章中学习的节点类创建的。我们创建一个 Node 对象,并创建另一个类来使用此 ode 对象。我们通过节点对象传递适当的值以指向下一个数据元素。下面的程序创建了包含三个数据元素的链表。在下一节中,我们将了解如何遍历链表。
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
list1 = SLinkedList()
list1.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list1.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
遍历链表
单链表只能从第一个数据元素开始向前遍历。我们只需通过将下一个节点的指针分配给当前数据元素来打印下一个数据元素的值。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
list.listprint()
输出
当执行上述代码时,它会产生以下结果:
Mon Tue Wed
在链表中插入
在链表中插入元素涉及重新分配现有节点到新插入节点的指针。根据新数据元素是在链表的开头、中间还是末尾插入,我们有以下几种情况。
在开头插入
这涉及将新数据节点的下一个指针指向链表的当前头部。因此,链表的当前头部成为第二个数据元素,而新节点成为链表的头部。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
def AtBegining(self,newdata):
NewNode = Node(newdata)
# Update the new nodes next val to existing node
NewNode.nextval = self.headval
self.headval = NewNode
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtBegining("Sun")
list.listprint()
输出
当执行上述代码时,它会产生以下结果:
Sun Mon Tue Wed
在末尾插入
这涉及将链表的当前最后一个节点的下一个指针指向新数据节点。因此,链表的当前最后一个节点成为倒数第二个数据节点,而新节点成为链表的最后一个节点。
示例
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add newnode
def AtEnd(self, newdata):
NewNode = Node(newdata)
if self.headval is None:
self.headval = NewNode
return
laste = self.headval
while(laste.nextval):
laste = laste.nextval
laste.nextval=NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtEnd("Thu")
list.listprint()
输出
当执行上述代码时,它会产生以下结果:
Mon Tue Wed Thu
在两个数据节点之间插入
这涉及更改特定节点的指针以指向新节点。这可以通过同时传递新节点和新节点将要插入其后的现有节点来实现。因此,我们定义了一个额外的类,它将更改新节点的下一个指针以指向中间节点的下一个指针。然后将新节点分配给中间节点的下一个指针。
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add node
def Inbetween(self,middle_node,newdata):
if middle_node is None:
print("The mentioned node is absent")
return
NewNode = Node(newdata)
NewNode.nextval = middle_node.nextval
middle_node.nextval = NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Thu")
list.headval.nextval = e2
e2.nextval = e3
list.Inbetween(list.headval.nextval,"Fri")
list.listprint()
输出
当执行上述代码时,它会产生以下结果:
Mon Tue Fri Thu
删除项目
我们可以使用节点的键来删除现有节点。在下面的程序中,我们找到要删除的节点的前一个节点。然后,将此节点的 next 指针指向要删除的节点的下一个节点。
示例
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLinkedList:
def __init__(self):
self.head = None
def Atbegining(self, data_in):
NewNode = Node(data_in)
NewNode.next = self.head
self.head = NewNode
# Function to remove node
def RemoveNode(self, Removekey):
HeadVal = self.head
if (HeadVal is not None):
if (HeadVal.data == Removekey):
self.head = HeadVal.next
HeadVal = None
return
while (HeadVal is not None):
if HeadVal.data == Removekey:
break
prev = HeadVal
HeadVal = HeadVal.next
if (HeadVal == None):
return
prev.next = HeadVal.next
HeadVal = None
def LListprint(self):
printval = self.head
while (printval):
print(printval.data),
printval = printval.next
llist = SLinkedList()
llist.Atbegining("Mon")
llist.Atbegining("Tue")
llist.Atbegining("Wed")
llist.Atbegining("Thu")
llist.RemoveNode("Tue")
llist.LListprint()
输出
当执行上述代码时,它会产生以下结果:
Thu Wed Mon
Python - 栈
在英语词典中,stack(栈)一词表示将物体一个叠一个地堆放。这与这种数据结构中内存的分配方式相同。它以类似于厨房里一堆盘子一个叠一个地存放的方式存储数据元素。因此,栈数据结构允许在一端进行操作,这可以称为栈的顶部。我们只能从此栈端添加或删除元素。
在栈中,最后插入的元素将首先出来,因为我们只能从栈顶删除。这种特性称为后进先出 (LIFO) 特性。添加和删除元素的操作称为 **PUSH** 和 **POP**。在下面的程序中,我们将其实现为 **add** 和 **remove** 函数。我们声明一个空列表,并使用 append() 和 pop() 方法来添加和删除数据元素。
将元素压入栈
让我们了解如何在栈中使用 PUSH。请参考下面提到的程序 -
示例
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use peek to look at the top of the stack
def peek(self):
return self.stack[-1]
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.peek()
print(AStack.peek())
AStack.add("Wed")
AStack.add("Thu")
print(AStack.peek())
输出
当执行上述代码时,它会产生以下结果:
Tue Thu
从栈中弹出元素
正如我们所知,我们只能从栈中删除最顶部的元素,我们实现了一个 Python 程序来执行此操作。以下程序中的 remove 函数返回最顶部的元素。我们首先计算栈的大小来检查顶部元素,然后使用内置的 pop() 方法找出最顶部的元素。
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use list pop method to remove element
def remove(self):
if len(self.stack) <= 0:
return ("No element in the Stack")
else:
return self.stack.pop()
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.add("Wed")
AStack.add("Thu")
print(AStack.remove())
print(AStack.remove())
输出
当执行上述代码时,它会产生以下结果:
Thu Wed
Python - 队列
我们在日常生活中都熟悉队列,因为我们等待服务。队列数据结构也意味着相同,其中数据元素按队列排列。队列的独特性在于添加和删除项目的方式。项目在一端允许,但在另一端删除。因此,它是一种先进先出方法。
可以使用 Python 列表实现队列,其中我们可以使用 insert() 和 pop() 方法添加和删除元素。没有插入,因为数据元素始终添加到队列的末尾。
添加元素
在下面的示例中,我们创建一个队列类,其中我们实现了先进先出方法。我们使用内置的 insert 方法添加数据元素。
示例
class Queue:
def __init__(self):
self.queue = list()
def addtoq(self,dataval):
# Insert method to add element
if dataval not in self.queue:
self.queue.insert(0,dataval)
return True
return False
def size(self):
return len(self.queue)
TheQueue = Queue()
TheQueue.addtoq("Mon")
TheQueue.addtoq("Tue")
TheQueue.addtoq("Wed")
print(TheQueue.size())
输出
当执行上述代码时,它会产生以下结果:
3
删除元素
在下面的示例中,我们创建一个队列类,其中我们插入数据,然后使用内置的 pop 方法删除数据。
示例
class Queue:
def __init__(self):
self.queue = list()
def addtoq(self,dataval):
# Insert method to add element
if dataval not in self.queue:
self.queue.insert(0,dataval)
return True
return False
# Pop method to remove element
def removefromq(self):
if len(self.queue)>0:
return self.queue.pop()
return ("No elements in Queue!")
TheQueue = Queue()
TheQueue.addtoq("Mon")
TheQueue.addtoq("Tue")
TheQueue.addtoq("Wed")
print(TheQueue.removefromq())
print(TheQueue.removefromq())
输出
当执行上述代码时,它会产生以下结果:
Mon Tue
Python - 双端队列
双端队列(或 deque)支持从任一端添加和删除元素。更常用的栈和队列是双端队列的简并形式,其中输入和输出限制在一端。
示例
import collections
DoubleEnded = collections.deque(["Mon","Tue","Wed"])
DoubleEnded.append("Thu")
print ("Appended at right - ")
print (DoubleEnded)
DoubleEnded.appendleft("Sun")
print ("Appended at right at left is - ")
print (DoubleEnded)
DoubleEnded.pop()
print ("Deleting from right - ")
print (DoubleEnded)
DoubleEnded.popleft()
print ("Deleting from left - ")
print (DoubleEnded)
输出
当执行上述代码时,它会产生以下结果:
Appended at right - deque(['Mon', 'Tue', 'Wed', 'Thu']) Appended at right at left is - deque(['Sun', 'Mon', 'Tue', 'Wed', 'Thu']) Deleting from right - deque(['Sun', 'Mon', 'Tue', 'Wed']) Deleting from left - deque(['Mon', 'Tue', 'Wed'])
Python - 高级链表
我们已经在前面章节中看到了链表,其中只能向前遍历。在本节中,我们看到另一种类型的链表,其中可以向前和向后遍历。这种链表称为双向链表。以下是双向链表的特点。
双向链表包含一个称为 first 和 last 的链接元素。
每个链接都包含一个数据字段和两个链接字段,称为 next 和 prev。
每个链接都使用其 next 链接与其下一个链接链接。
每个链接都使用其 previous 链接与其上一个链接链接。
最后一个链接带有 null 链接以标记列表的末尾。
创建双向链表
我们使用 Node 类创建双向链表。现在我们使用与单向链表中相同的方法,但 head 和 next 指针将用于正确分配,以在每个节点中创建两个链接,此外还有节点中存在的数据。
示例
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
class doubly_linked_list:
def __init__(self):
self.head = None
# Adding data elements
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Print the Doubly Linked list
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.push(8)
dllist.push(62)
dllist.listprint(dllist.head)
输出
当执行上述代码时,它会产生以下结果:
62 8 12
插入双向链表
在这里,我们将了解如何使用以下程序将节点插入双向链表。该程序使用名为 insert 的方法,该方法将新节点插入双向链表头部的第三个位置。
示例
# Create the Node class
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
# Create the doubly linked list
class doubly_linked_list:
def __init__(self):
self.head = None
# Define the push method to add elements
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Define the insert method to insert the element
def insert(self, prev_node, NewVal):
if prev_node is None:
return
NewNode = Node(NewVal)
NewNode.next = prev_node.next
prev_node.next = NewNode
NewNode.prev = prev_node
if NewNode.next is not None:
NewNode.next.prev = NewNode
# Define the method to print the linked list
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.push(8)
dllist.push(62)
dllist.insert(dllist.head.next, 13)
dllist.listprint(dllist.head)
输出
当执行上述代码时,它会产生以下结果:
62 8 13 12
追加到双向链表
追加到双向链表将把元素添加到末尾。
示例
# Create the node class
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
# Create the doubly linked list class
class doubly_linked_list:
def __init__(self):
self.head = None
# Define the push method to add elements at the begining
def push(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = self.head
if self.head is not None:
self.head.prev = NewNode
self.head = NewNode
# Define the append method to add elements at the end
def append(self, NewVal):
NewNode = Node(NewVal)
NewNode.next = None
if self.head is None:
NewNode.prev = None
self.head = NewNode
return
last = self.head
while (last.next is not None):
last = last.next
last.next = NewNode
NewNode.prev = last
return
# Define the method to print
def listprint(self, node):
while (node is not None):
print(node.data),
last = node
node = node.next
dllist = doubly_linked_list()
dllist.push(12)
dllist.append(9)
dllist.push(8)
dllist.push(62)
dllist.append(45)
dllist.listprint(dllist.head)
输出
当执行上述代码时,它会产生以下结果:
62 8 12 9 45
请注意追加操作中元素 9 和 45 的位置。
Python - 哈希表
哈希表是一种数据结构,其中数据元素的地址或索引值是由哈希函数生成的。这使得访问数据更快,因为索引值充当数据值的键。换句话说,哈希表存储键值对,但键是通过哈希函数生成的。
因此,数据元素的搜索和插入函数变得更快,因为键值本身成为存储数据的数组的索引。
在 Python 中,字典数据类型表示哈希表的实现。字典中的键满足以下要求。
字典的键是可哈希的,即它们是由哈希函数生成的,该哈希函数为提供给它的每个唯一值生成唯一的结果。
字典中数据元素的顺序不固定。
因此,我们看到如下使用字典数据类型实现哈希表。
访问字典中的值
要访问字典元素,您可以使用熟悉的方括号以及键来获取其值。
示例
# Declare a dictionary
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
# Accessing the dictionary with its key
print ("dict['Name']: ", dict['Name'])
print ("dict['Age']: ", dict['Age'])
输出
当执行上述代码时,它会产生以下结果:
dict['Name']: Zara dict['Age']: 7
更新字典
您可以通过添加新条目或键值对、修改现有条目或删除现有条目来更新字典,如下面的简单示例所示:
示例
# Declare a dictionary
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
dict['Age'] = 8; # update existing entry
dict['School'] = "DPS School"; # Add new entry
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
输出
当执行上述代码时,它会产生以下结果:
dict['Age']: 8 dict['School']: DPS School
删除字典元素
您可以删除单个字典元素或清除字典的全部内容。您也可以在单个操作中删除整个字典。要显式删除整个字典,只需使用 del 语句。
示例
dict = {'Name': 'Zara', 'Age': 7, 'Class': 'First'}
del dict['Name']; # remove entry with key 'Name'
dict.clear(); # remove all entries in dict
del dict ; # delete entire dictionary
print ("dict['Age']: ", dict['Age'])
print ("dict['School']: ", dict['School'])
输出
这将产生以下结果。请注意,由于 del dict 后字典不再存在,因此会引发异常。
dict['Age']: dict['Age'] dict['School']: dict['School']
Python - 二叉树
树表示由边连接的节点。它是一种非线性数据结构。它具有以下属性 -
一个节点被标记为根节点。
除根节点外的每个节点都与一个父节点相关联。
每个节点可以有任意数量的子节点。
我们通过使用前面讨论的节点概念在 Python 中创建树数据结构。我们指定一个节点作为根节点,然后添加更多节点作为子节点。以下是创建根节点的程序。
创建根节点
我们只创建一个 Node 类并为节点分配一个值。这成为只有一棵根节点的树。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def PrintTree(self):
print(self.data)
root = Node(10)
root.PrintTree()
输出
当执行上述代码时,它会产生以下结果:
10
插入树
要插入树,我们使用上面创建的相同 Node 类,并向其中添加 insert 类。insert 类将节点的值与父节点的值进行比较,并决定将其添加为左节点还是右节点。最后,PrintTree 类用于打印树。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
# Compare the new value with the parent node
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Use the insert method to add nodes
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)
root.PrintTree()
输出
当执行上述代码时,它会产生以下结果:
3 6 12 14
遍历树
可以通过决定访问每个节点的顺序来遍历树。正如我们清楚地看到的那样,我们可以从一个节点开始,然后先访问左子树,然后访问右子树。或者我们也可以先访问右子树,然后访问左子树。因此,这些树遍历方法有不同的名称。
树遍历算法
遍历是访问树的所有节点的过程,也可能打印它们的值。因为所有节点都通过边(链接)连接,所以我们总是从根(头部)节点开始。也就是说,我们无法随机访问树中的节点。我们使用三种方法来遍历树。
中序遍历
先序遍历
后序遍历
中序遍历
在这种遍历方法中,先访问左子树,然后访问根节点,最后访问右子树。我们应该始终记住,每个节点都可以表示一个子树本身。
在下面的 Python 程序中,我们使用 Node 类为根节点以及左节点和右节点创建占位符。然后,我们创建一个 insert 函数将数据添加到树中。最后,通过创建一个空列表并将左节点首先添加到列表中,然后是根节点或父节点,实现了中序遍历逻辑。
最后,添加左节点以完成中序遍历。请注意,此过程会针对每个子树重复,直到遍历所有节点。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Inorder traversal
# Left -> Root -> Right
def inorderTraversal(self, root):
res = []
if root:
res = self.inorderTraversal(root.left)
res.append(root.data)
res = res + self.inorderTraversal(root.right)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.inorderTraversal(root))
输出
当执行上述代码时,它会产生以下结果:
[10, 14, 19, 27, 31, 35, 42]
先序遍历
在这种遍历方法中,先访问根节点,然后访问左子树,最后访问右子树。
在下面的 Python 程序中,我们使用 Node 类为根节点以及左节点和右节点创建占位符。然后,我们创建一个 insert 函数将数据添加到树中。最后,通过创建一个空列表并将根节点首先添加到列表中,然后是左节点,实现了先序遍历逻辑。
最后,添加右节点以完成先序遍历。请注意,此过程会针对每个子树重复,直到遍历所有节点。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Preorder traversal
# Root -> Left ->Right
def PreorderTraversal(self, root):
res = []
if root:
res.append(root.data)
res = res + self.PreorderTraversal(root.left)
res = res + self.PreorderTraversal(root.right)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.PreorderTraversal(root))
输出
当执行上述代码时,它会产生以下结果:
[27, 14, 10, 19, 35, 31, 42]
后序遍历
在这种遍历方法中,最后访问根节点,因此得名。首先,我们遍历左子树,然后遍历右子树,最后遍历根节点。
在下面的 Python 程序中,我们使用 Node 类为根节点以及左节点和右节点创建占位符。然后,我们创建一个 insert 函数将数据添加到树中。最后,通过创建一个空列表并将左节点首先添加到列表中,然后是右节点,实现了后序遍历逻辑。
最后,添加根节点或父节点以完成后序遍历。请注意,此过程会针对每个子树重复,直到遍历所有节点。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert Node
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else if data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Postorder traversal
# Left ->Right -> Root
def PostorderTraversal(self, root):
res = []
if root:
res = self.PostorderTraversal(root.left)
res = res + self.PostorderTraversal(root.right)
res.append(root.data)
return res
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(10)
root.insert(19)
root.insert(31)
root.insert(42)
print(root.PostorderTraversal(root))
输出
当执行上述代码时,它会产生以下结果:
[10, 19, 14, 31, 42, 35, 27]
Python - 搜索树
二叉搜索树 (BST) 是一种树,其中所有节点都遵循以下提到的属性。节点的左子树的键小于或等于其父节点的键。节点的右子树的键大于其父节点的键。因此,BST 将其所有子树划分为两个部分;左子树和右子树。
left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)
在 B 树中搜索值
在树中搜索值涉及将传入值与退出节点的值进行比较。这里我们也从左到右遍历节点,最后再与父节点比较。如果要搜索的值与任何现有值都不匹配,则返回“未找到”消息,否则返回“已找到”消息。
示例
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
else data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# findval method to compare the value with nodes
def findval(self, lkpval):
if lkpval < self.data:
if self.left is None:
return str(lkpval)+" Not Found"
return self.left.findval(lkpval)
else if lkpval > self.data:
if self.right is None:
return str(lkpval)+" Not Found"
return self.right.findval(lkpval)
else:
print(str(self.data) + ' is found')
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)
print(root.findval(7))
print(root.findval(14))
输出
当执行上述代码时,它会产生以下结果:
7 Not Found 14 is found
Python - 堆
堆是一种特殊的树结构,其中每个父节点都小于或等于其子节点。然后它被称为最小堆。如果每个父节点都大于或等于其子节点,则它被称为最大堆。它在实现优先级队列中非常有用,其中权重较高的队列项在处理中具有更高的优先级。
我们网站上提供了有关堆的详细讨论。如果您不熟悉堆数据结构,请先学习它。在本节中,我们将看到使用 Python 实现堆数据结构。
创建堆
堆是使用 Python 的内置库 heapq 创建的。该库具有执行堆数据结构上各种操作的相关函数。以下是这些函数的列表。
**heapify** - 此函数将常规列表转换为堆。在生成的堆中,最小的元素被推送到索引位置 0。但其余数据元素不一定排序。
**heappush** - 此函数将元素添加到堆中,而不会更改当前堆。
**heappop** - 此函数从堆中返回最小的数据元素。
**heapreplace** - 此函数用函数中提供的新值替换最小的数据元素。
创建堆
堆的创建只需使用一个包含元素的列表和堆化函数即可。在下面的示例中,我们提供了一个元素列表,堆化函数会重新排列元素,并将最小的元素放到第一个位置。
示例
import heapq H = [21,1,45,78,3,5] # Use heapify to rearrange the elements heapq.heapify(H) print(H)
输出
当执行上述代码时,它会产生以下结果:
[1, 3, 5, 78, 21, 45]
插入堆
将数据元素插入堆中总是将元素添加到最后一个索引处。但是,您可以再次应用堆化函数,仅当新添加的元素值最小时,才能将其放到第一个索引位置。在下面的示例中,我们插入数字 8。
示例
import heapq H = [21,1,45,78,3,5] # Covert to a heap heapq.heapify(H) print(H) # Add element heapq.heappush(H,8) print(H)
输出
当执行上述代码时,它会产生以下结果:
[1, 3, 5, 78, 21, 45] [1, 3, 5, 78, 21, 45, 8]
从堆中删除
您可以使用此函数删除第一个索引处的元素。在下面的示例中,该函数将始终删除索引位置 1 处的元素。
示例
import heapq H = [21,1,45,78,3,5] # Create the heap heapq.heapify(H) print(H) # Remove element from the heap heapq.heappop(H) print(H)
输出
当执行上述代码时,它会产生以下结果:
[1, 3, 5, 78, 21, 45] [3, 21, 5, 78, 45]
在堆中替换
堆替换函数始终删除堆中最小的元素,并将新传入的元素插入到某个位置,该位置不受任何顺序的限制。
示例
import heapq H = [21,1,45,78,3,5] # Create the heap heapq.heapify(H) print(H) # Replace an element heapq.heapreplace(H,6) print(H)
输出
当执行上述代码时,它会产生以下结果:
[1, 3, 5, 78, 21, 45] [3, 6, 5, 78, 21, 45]
Python - 图
图是对象集合的图形表示,其中某些对象对通过链接连接。相互连接的对象由称为顶点的点表示,连接顶点的链接称为边。与图相关的各种术语和功能在我们的教程中进行了详细描述。
在本章中,我们将学习如何使用 Python 程序创建图并在其中添加各种数据元素。以下是我们在图上执行的基本操作。
- 显示图的顶点
- 显示图的边
- 添加顶点
- 添加边
- 创建图
可以使用 Python 字典数据类型轻松地表示图。我们将顶点表示为字典的键,将顶点之间的连接(也称为边)表示为字典中的值。
请看以下图形:
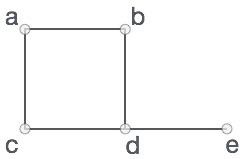
在上图中,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
示例
我们可以在 Python 程序中如下表示此图:
# Create the dictionary with graph elements
graph = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
# Print the graph
print(graph)
输出
当执行上述代码时,它会产生以下结果:
{'c': ['a', 'd'], 'a': ['b', 'c'], 'e': ['d'], 'd': ['e'], 'b': ['a', 'd']}
显示图的顶点
要显示图的顶点,我们只需查找图字典的键。我们使用 keys() 方法。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = []
self.gdict = gdict
# Get the keys of the dictionary
def getVertices(self):
return list(self.gdict.keys())
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
print(g.getVertices())
输出
当执行上述代码时,它会产生以下结果:
['d', 'b', 'e', 'c', 'a']
显示图的边
查找图的边比顶点稍微复杂一些,因为我们必须找到每对顶点之间是否存在边。因此,我们创建一个空的边列表,然后遍历与每个顶点关联的边值。形成一个列表,其中包含从顶点找到的不同边组。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def edges(self):
return self.findedges()
# Find the distinct list of edges
def findedges(self):
edgename = []
for vrtx in self.gdict:
for nxtvrtx in self.gdict[vrtx]:
if {nxtvrtx, vrtx} not in edgename:
edgename.append({vrtx, nxtvrtx})
return edgename
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
print(g.edges())
输出
当执行上述代码时,它会产生以下结果:
[{'b', 'a'}, {'b', 'd'}, {'e', 'd'}, {'a', 'c'}, {'c', 'd'}]
添加顶点
添加顶点很简单,我们只需向图字典添加另一个键即可。
示例
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def getVertices(self):
return list(self.gdict.keys())
# Add the vertex as a key
def addVertex(self, vrtx):
if vrtx not in self.gdict:
self.gdict[vrtx] = []
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
g.addVertex("f")
print(g.getVertices())
输出
当执行上述代码时,它会产生以下结果:
['a', 'b', 'c', 'd', 'e','f']
添加边
向现有图中添加边涉及将新顶点视为元组,并验证边是否已存在。如果不存在,则添加边。
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def edges(self):
return self.findedges()
# Add the new edge
def AddEdge(self, edge):
edge = set(edge)
(vrtx1, vrtx2) = tuple(edge)
if vrtx1 in self.gdict:
self.gdict[vrtx1].append(vrtx2)
else:
self.gdict[vrtx1] = [vrtx2]
# List the edge names
def findedges(self):
edgename = []
for vrtx in self.gdict:
for nxtvrtx in self.gdict[vrtx]:
if {nxtvrtx, vrtx} not in edgename:
edgename.append({vrtx, nxtvrtx})
return edgename
# Create the dictionary with graph elements
graph_elements = {
"a" : ["b","c"],
"b" : ["a", "d"],
"c" : ["a", "d"],
"d" : ["e"],
"e" : ["d"]
}
g = graph(graph_elements)
g.AddEdge({'a','e'})
g.AddEdge({'a','c'})
print(g.edges())
输出
当执行上述代码时,它会产生以下结果:
[{'e', 'd'}, {'b', 'a'}, {'b', 'd'}, {'a', 'c'}, {'a', 'e'}, {'c', 'd'}]
Python - 算法设计
算法是一个逐步的过程,它定义了一组指令,这些指令按特定顺序执行以获得所需的输出。算法通常独立于底层语言创建,即,算法可以在多种编程语言中实现。
从数据结构的角度来看,以下是一些重要的算法类别:
搜索 - 在数据结构中搜索项目的算法。
排序 - 按特定顺序对项目进行排序的算法。
插入 - 将项目插入数据结构的算法。
更新 - 更新数据结构中现有项目的算法。
删除 - 从数据结构中删除现有项目的算法。
算法的特征
并非所有过程都可以称为算法。算法应具有以下特征:
明确性 - 算法应清晰明确。它的每个步骤(或阶段)及其输入/输出都应清晰,并且必须只产生一个含义。
输入 - 算法应具有 0 个或多个明确定义的输入。
输出 - 算法应具有 1 个或多个明确定义的输出,并且应与所需的输出匹配。
有限性 - 算法必须在有限的步骤后终止。
可行性 - 应在可用资源下可行。
独立性 - 算法应具有分步说明,这些说明应独立于任何编程代码。
如何编写算法?
没有编写算法的明确标准。相反,它取决于问题和资源。算法永远不会编写为支持特定的编程代码。
众所周知,所有编程语言都共享基本的代码结构,如循环(do、for、while)、流程控制(if-else)等。这些通用结构可用于编写算法。
我们以分步方式编写算法,但这并非总是如此。算法编写是一个过程,在问题域明确定义后执行。也就是说,我们应该知道我们正在为其设计解决方案的问题域。
示例
让我们尝试通过一个示例学习算法编写。
问题 - 设计一个算法来添加两个数字并显示结果。
步骤 1 - 开始
步骤 2 - 声明三个整数 a、b 和 c
步骤 3 - 定义 a 和 b 的值
步骤 4 - 添加 a 和 b 的值
步骤 5 - 将步骤 4的输出存储到 c 中
步骤 6 - 打印 c
步骤 7 - 停止
算法告诉程序员如何编写程序。或者,算法可以写成:
步骤 1 - 开始添加
步骤 2 - 获取 a 和 b 的值
步骤 3 - c ← a + b
步骤 4 - 显示 c
步骤 5 - 停止
在算法的设计和分析中,通常使用第二种方法来描述算法。它使分析师能够轻松地分析算法,而忽略所有不需要的定义。他可以观察正在使用的操作以及流程是如何流动的。
编写步骤编号是可选的。
我们设计算法来获得给定问题的解决方案。一个问题可以通过多种方式解决。
因此,对于给定问题,可以推导出许多解决方案算法。下一步是分析这些提出的解决方案算法并实现最合适的解决方案。
Python - 分治法
在分治法中,手头的难题被分解成更小的子问题,然后每个问题都独立解决。当我们继续将子问题分解成更小的子问题时,我们最终可能会达到无法再进行分解的阶段。这些“原子”最小的子问题(部分)得到解决。最后合并所有子问题的解决方案,以获得原始问题的解决方案。
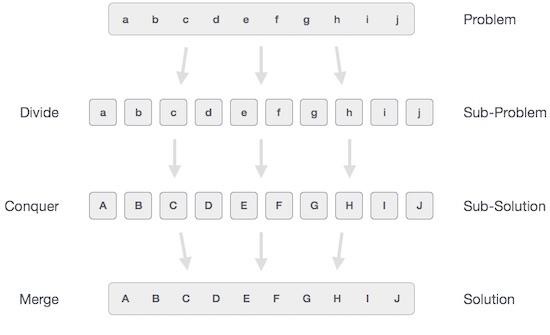
从广义上讲,我们可以将分治方法理解为一个三步过程。
分/分解
此步骤涉及将问题分解成更小的子问题。子问题应代表原始问题的一部分。此步骤通常采用递归方法来划分问题,直到没有子问题可以进一步划分。在此阶段,子问题变得具有原子性,但仍然代表实际问题的一部分。
解决/求解
此步骤接收大量需要解决的较小子问题。通常,在此级别,问题被认为是“自行解决”的。
合并/组合
当较小子问题得到解决时,此阶段递归地将它们组合起来,直到它们形成原始问题的解决方案。这种算法方法以递归方式工作,并且解决和合并步骤非常接近,以至于它们看起来像一个。
示例
以下程序是分治编程方法的一个示例,其中使用 Python 实现二分查找。
二分查找实现
在二分查找中,我们取一个排序的元素列表,并从列表中间开始查找元素。如果搜索值与列表中的中间值匹配,则我们完成搜索。否则,我们通过选择继续处理列表的右侧或左侧一半来消除一半的元素列表,具体取决于搜索项目的价值。
这是可能的,因为列表已排序,并且比线性搜索快得多。在这里,我们划分给定的列表并通过选择列表的适当一半来征服。我们重复此方法,直到找到元素或得出关于其在列表中不存在的结论。
示例
def bsearch(list, val):
list_size = len(list) - 1
idx0 = 0
idxn = list_size
# Find the middle most value
while idx0 <= idxn:
midval = (idx0 + idxn)// 2
if list[midval] == val:
return midval
# Compare the value the middle most value
if val > list[midval]:
idx0 = midval + 1
else:
idxn = midval - 1
if idx0 > idxn:
return None
# Initialize the sorted list
list = [2,7,19,34,53,72]
# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))
输出
当执行上述代码时,它会产生以下结果:
5 None
Python - 递归
递归允许函数调用自身。代码的固定步骤会针对新值重复执行。我们还必须设置标准来决定递归调用何时结束。在下面的示例中,我们看到了二分查找的递归方法。我们取一个排序的列表,并将其索引范围作为输入提供给递归函数。
使用递归的二分查找
我们使用 Python 实现二分查找算法,如下所示。我们使用一个有序的项目列表,并设计一个递归函数,以列表以及起始和结束索引作为输入。然后,二分查找函数会自行调用,直到找到搜索的项目或得出关于其在列表中不存在的结论。
示例
def bsearch(list, idx0, idxn, val):
if (idxn < idx0):
return None
else:
midval = idx0 + ((idxn - idx0) // 2)
# Compare the search item with middle most value
if list[midval] > val:
return bsearch(list, idx0, midval-1,val)
else if list[midval] < val:
return bsearch(list, midval+1, idxn, val)
else:
return midval
list = [8,11,24,56,88,131]
print(bsearch(list, 0, 5, 24))
print(bsearch(list, 0, 5, 51))
输出
当执行上述代码时,它会产生以下结果:
2 None
Python - 回溯法
回溯是一种递归形式。但它只涉及从任何可能性中选择一个选项。我们首先选择一个选项,如果我们到达一个状态,我们得出结论,这个特定选项没有给出所需的解决方案,则从该选项回溯。我们通过遍历每个可用选项重复这些步骤,直到我们获得所需的解决方案。
下面是一个查找给定字母集的所有可能的排列顺序的示例。当我们选择一对时,我们应用回溯来验证该确切的对是否已创建。如果尚未创建,则将该对添加到答案列表中,否则将其忽略。
示例
def permute(list, s):
if list == 1:
return s
else:
return [
y + x
for y in permute(1, s)
for x in permute(list - 1, s)
]
print(permute(1, ["a","b","c"]))
print(permute(2, ["a","b","c"]))
输出
当执行上述代码时,它会产生以下结果:
['a', 'b', 'c'] ['aa', 'ab', 'ac', 'ba', 'bb', 'bc', 'ca', 'cb', 'cc']
Python - 排序算法
排序是指以特定格式排列数据。排序算法指定以特定顺序排列数据的方式。最常见的顺序是按数字或字典顺序。
排序的重要性在于,如果数据以排序的方式存储,则可以将数据搜索优化到非常高的水平。排序还用于以更易读的格式表示数据。下面我们看到五种在 Python 中实现排序的方法。
冒泡排序
归并排序
插入排序
希尔排序
选择排序
冒泡排序
这是一种基于比较的算法,其中比较每对相邻元素,如果不按顺序排列,则交换元素。
示例
def bubblesort(list):
# Swap the elements to arrange in order
for iter_num in range(len(list)-1,0,-1):
for idx in range(iter_num):
if list[idx]>list[idx+1]:
temp = list[idx]
list[idx] = list[idx+1]
list[idx+1] = temp
list = [19,2,31,45,6,11,121,27]
bubblesort(list)
print(list)
输出
当执行上述代码时,它会产生以下结果:
[2, 6, 11, 19, 27, 31, 45, 121]
归并排序
归并排序首先将数组分成相等的两半,然后以排序的方式将它们组合起来。
示例
def merge_sort(unsorted_list):
if len(unsorted_list) <= 1:
return unsorted_list
# Find the middle point and devide it
middle = len(unsorted_list) // 2
left_list = unsorted_list[:middle]
right_list = unsorted_list[middle:]
left_list = merge_sort(left_list)
right_list = merge_sort(right_list)
return list(merge(left_list, right_list))
# Merge the sorted halves
def merge(left_half,right_half):
res = []
while len(left_half) != 0 and len(right_half) != 0:
if left_half[0] < right_half[0]:
res.append(left_half[0])
left_half.remove(left_half[0])
else:
res.append(right_half[0])
right_half.remove(right_half[0])
if len(left_half) == 0:
res = res + right_half
else:
res = res + left_half
return res
unsorted_list = [64, 34, 25, 12, 22, 11, 90]
print(merge_sort(unsorted_list))
输出
当执行上述代码时,它会产生以下结果:
[11, 12, 22, 25, 34, 64, 90]
插入排序
插入排序包括在已排序列表中找到给定元素的正确位置。因此,在开始时,我们比较前两个元素并通过比较它们来排序。然后我们选择第三个元素,并在前两个已排序元素中找到其正确位置。这样,我们逐渐继续将更多元素添加到已排序列表中,方法是将它们放在其正确的位置。
示例
def insertion_sort(InputList):
for i in range(1, len(InputList)):
j = i-1
nxt_element = InputList[i]
# Compare the current element with next one
while (InputList[j] > nxt_element) and (j >= 0):
InputList[j+1] = InputList[j]
j=j-1
InputList[j+1] = nxt_element
list = [19,2,31,45,30,11,121,27]
insertion_sort(list)
print(list)
输出
当执行上述代码时,它会产生以下结果:
[19, 2, 31, 45, 30, 11, 27, 121]
希尔排序
希尔排序涉及对彼此远离的元素进行排序。我们对给定列表的大子列表进行排序,并继续减小子列表的大小,直到所有元素都排序。下面的程序通过将其与列表大小长度的一半相等来找到间隔,然后开始对其中的所有元素进行排序。然后我们继续重置间隔,直到整个列表排序。
示例
def shellSort(input_list):
gap = len(input_list) // 2
while gap > 0:
for i in range(gap, len(input_list)):
temp = input_list[i]
j = i
# Sort the sub list for this gap
while j >= gap and input_list[j - gap] > temp:
input_list[j] = input_list[j - gap]
j = j-gap
input_list[j] = temp
# Reduce the gap for the next element
gap = gap//2
list = [19,2,31,45,30,11,121,27]
shellSort(list)
print(list)
输出
当执行上述代码时,它会产生以下结果:
[2, 11, 19, 27, 30, 31, 45, 121]
选择排序
在选择排序中,我们首先在给定列表中找到最小值,并将其移动到已排序列表。然后我们对无序列表中每个剩余元素重复此过程。进入已排序列表的下一个元素与现有元素进行比较,并放置在其正确的位置。因此,最后所有来自无序列表的元素都已排序。
示例
def selection_sort(input_list):
for idx in range(len(input_list)):
min_idx = idx
for j in range( idx +1, len(input_list)):
if input_list[min_idx] > input_list[j]:
min_idx = j
# Swap the minimum value with the compared value
input_list[idx], input_list[min_idx] = input_list[min_idx], input_list[idx]
l = [19,2,31,45,30,11,121,27]
selection_sort(l)
print(l)
输出
当执行上述代码时,它会产生以下结果:
[19, 2, 31, 45, 30, 11, 121, 27]
Python - 搜索算法
当您将数据存储在不同的数据结构中时,搜索是一个非常基本的需求。最简单的方法是遍历数据结构中的每个元素,并将其与您要搜索的值进行匹配。这称为线性搜索。它效率低下且很少使用,但为此创建程序可以让我们了解如何实现一些高级搜索算法。
线性搜索
在这种类型的搜索中,对所有项目依次进行顺序搜索。检查每个项目,如果找到匹配项,则返回该特定项目,否则搜索将继续到数据结构的末尾。
示例
def linear_search(values, search_for):
search_at = 0
search_res = False
# Match the value with each data element
while search_at < len(values) and search_res is False:
if values[search_at] == search_for:
search_res = True
else:
search_at = search_at + 1
return search_res
l = [64, 34, 25, 12, 22, 11, 90]
print(linear_search(l, 12))
print(linear_search(l, 91))
输出
当执行上述代码时,它会产生以下结果:
True False
插值搜索
此搜索算法基于所需值的探测位置。为了使此算法正常工作,数据集合应以排序形式且均匀分布。最初,探测位置是集合中最中间项目的的位置。如果发生匹配,则返回项目的索引。如果中间项目大于该项目,则在中间项目右侧的子数组中再次计算探测位置。否则,在中间项目左侧的子数组中搜索该项目。此过程也继续在子数组上进行,直到子数组的大小减小到零。
示例
有一个特定的公式来计算中间位置,如下面的程序所示。
def intpolsearch(values,x ):
idx0 = 0
idxn = (len(values) - 1)
while idx0 <= idxn and x >= values[idx0] and x <= values[idxn]:
# Find the mid point
mid = idx0 +\
int(((float(idxn - idx0)/( values[idxn] - values[idx0]))
* ( x - values[idx0])))
# Compare the value at mid point with search value
if values[mid] == x:
return "Found "+str(x)+" at index "+str(mid)
if values[mid] < x:
idx0 = mid + 1
return "Searched element not in the list"
l = [2, 6, 11, 19, 27, 31, 45, 121]
print(intpolsearch(l, 2))
输出
当执行上述代码时,它会产生以下结果:
Found 2 at index 0
Python - 图算法
图是在解决许多重要的数学挑战时非常有用的数据结构。例如,计算机网络拓扑或分析化学化合物的分子结构。它们还用于城市交通或路线规划,甚至用于人类语言及其语法。所有这些应用程序都面临着一个共同的挑战,即使用其边遍历图并确保访问图的所有节点。有两种常用的方法可以执行此遍历,如下所述。
深度优先遍历
也称为深度优先搜索 (DFS),此算法以深度方向遍历图,并使用堆栈来记住在任何迭代中发生死锁时开始搜索的下一个顶点。我们使用集合数据类型在 Python 中为图实现 DFS,因为它们提供了跟踪已访问和未访问节点所需的函数。
示例
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
# Check for the visisted and unvisited nodes
def dfs(graph, start, visited = None):
if visited is None:
visited = set()
visited.add(start)
print(start)
for next in graph[start] - visited:
dfs(graph, next, visited)
return visited
gdict = {
"a" : set(["b","c"]),
"b" : set(["a", "d"]),
"c" : set(["a", "d"]),
"d" : set(["e"]),
"e" : set(["a"])
}
dfs(gdict, 'a')
输出
当执行上述代码时,它会产生以下结果:
a b d e c
广度优先遍历
也称为广度优先搜索 (BFS),此算法以广度方向遍历图,并使用队列来记住在任何迭代中发生死锁时开始搜索的下一个顶点。请访问我们网站中的此链接以了解图的 BFS 步骤的详细信息。
我们使用前面讨论的队列数据结构在 Python 中为图实现 BFS。当我们继续访问相邻的未访问节点并将其添加到队列中时。然后我们仅开始出队没有未访问节点的节点。当没有下一个要访问的相邻节点时,我们停止程序。
示例
import collections
class graph:
def __init__(self,gdict=None):
if gdict is None:
gdict = {}
self.gdict = gdict
def bfs(graph, startnode):
# Track the visited and unvisited nodes using queue
seen, queue = set([startnode]), collections.deque([startnode])
while queue:
vertex = queue.popleft()
marked(vertex)
for node in graph[vertex]:
if node not in seen:
seen.add(node)
queue.append(node)
def marked(n):
print(n)
# The graph dictionary
gdict = {
"a" : set(["b","c"]),
"b" : set(["a", "d"]),
"c" : set(["a", "d"]),
"d" : set(["e"]),
"e" : set(["a"])
}
bfs(gdict, "a")
输出
当执行上述代码时,它会产生以下结果:
a c b d e
Python - 算法分析
可以在两个不同的阶段分析算法的效率,即实现之前和实现之后。它们如下所述。
先验分析 - 这是对算法的理论分析。通过假设所有其他因素(例如处理器速度)都是恒定的并且对实现没有影响来衡量算法的效率。
后验分析 - 这是对算法的经验分析。使用编程语言实现所选算法。然后在目标计算机上执行此操作。在此分析中,收集实际统计信息,例如运行时间和所需空间。
算法复杂度
假设X是一个算法,n是输入数据的大小,算法 X 使用的时间和空间是决定 X 效率的两个主要因素。
时间因素 - 通过计算关键操作的数量(例如排序算法中的比较)来衡量时间。
空间因素 - 通过计算算法所需的最大内存空间来衡量空间。
算法f(n)的复杂度以n(作为输入数据的大小)给出算法的运行时间和/或存储空间。
空间复杂度
算法的空间复杂度表示算法在其生命周期中所需的内存空间量。算法所需的空间等于以下两个组件的总和。
一个固定部分,即用于存储某些数据和变量的空间,这些数据和变量与问题的规模无关。例如,使用的简单变量和常量、程序大小等。
一个可变部分,即由变量所需的空间,其大小取决于问题的规模。例如,动态内存分配、递归堆栈空间等。
任何算法 P 的空间复杂度 S(P) 为 S(P) = C + SP(I),其中 C 是固定部分,S(I) 是算法的可变部分,它取决于实例特征 I。以下是一个简单的示例,试图解释这个概念。
算法:SUM(A, B)
步骤 1 - 开始
步骤 2 - C ← A + B + 10
步骤 3 - 停止
这里我们有三个变量 A、B 和 C 以及一个常量。因此 S(P) = 1 + 3。现在,空间取决于给定变量和常量类型的数据类型,并且将相应地乘以它。
时间复杂度
算法的时间复杂度表示算法运行到完成所需的时间量。时间需求可以定义为数值函数 T(n),其中 T(n) 可以衡量为步骤数,前提是每个步骤消耗恒定时间。
例如,两个 n 位整数的加法需要n个步骤。因此,总计算时间为 T(n) = c ∗ n,其中 c 是两个位加法所需的时间。在这里,我们观察到 T(n) 随着输入大小的增加而线性增长。
Python - 算法类型
必须分析算法的效率和准确性才能比较它们并在某些情况下选择特定的算法。进行此分析的过程称为渐近分析。它指的是用数学计算单位计算任何操作的运行时间。
例如,一个操作的运行时间计算为 f(n),另一个操作的运行时间计算为 g(n2)。这意味着第一个操作的运行时间将随着 n 的增加而线性增加,而第二个操作的运行时间将在 n 增加时呈指数增长。同样,如果 n 非常小,则两个操作的运行时间将几乎相同。
通常,算法所需的时间分为三种类型。
最佳情况 - 程序执行所需的最小时间。
平均情况 - 程序执行所需的平均时间。
最坏情况 - 程序执行所需的最大时间。
渐近表示法
常用的渐近表示法来计算算法的运行时间复杂度。
Ο 表示法
Ω 表示法
θ 表示法
大 O 表示法,Ο
Ο(n) 表示法是表达算法运行时间上界的正式方法。它衡量最坏情况时间复杂度或算法可能完成所需的最长时间。
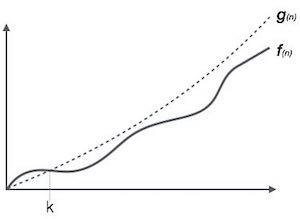
例如,对于函数f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
Omega 表示法,Ω
Ω(n) 表示法是表达算法运行时间下界的正式方法。它衡量最佳情况时间复杂度或算法可能完成所需的最短时间。
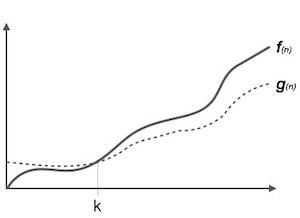
例如,对于函数f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
Theta 表示法,θ
θ(n) 表示法是表达算法运行时间下界和上界的正式方法。它表示如下。
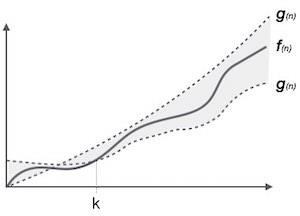
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
常用渐近表示法
下面列出了一些常用的渐近表示法。
| 常数 | — | Ο(1) |
| 对数 | — | Ο(log n) |
| 线性 | — | Ο(n) |
| n log n | — | Ο(n log n) |
| 二次 | — | Ο(n2) |
| 三次 | — | Ο(n3) |
| 多项式 | — | nΟ(1) |
| 指数 | — | 2Ο(n) |
Python - 算法类别
算法是不明确的步骤,应该通过处理零个或多个输入来为我们提供明确的输出。这导致了在设计和编写算法方面的许多方法。据观察,大多数算法可以分为以下几类。
贪心算法
贪婪算法试图找到局部最优解,这最终可能导致全局最优解。但是,通常贪婪算法并不能提供全局最优解。
因此,贪婪算法在那个时间点寻找一个简单的解决方案,而不考虑它如何影响未来的步骤。这类似于人类在没有完全了解所提供输入的情况下解决问题的方式。
大多数网络算法都使用贪婪方法。以下是一些示例:
旅行商问题
Prim 最小生成树算法
Kruskal 最小生成树算法
Dijkstra 最小生成树算法
分治法
这类算法涉及将给定问题分解成更小的子问题,然后独立地解决每个子问题。当问题无法进一步细分时,我们开始合并每个子问题的解决方案,以得出更大问题的解决方案。
分治算法的重要示例包括:
归并排序
快速排序
Kruskal 最小生成树算法
二分查找
动态规划
动态规划也涉及将更大的问题分解成更小的子问题,但与分治法不同,它不涉及独立地解决每个子问题。相反,它会记住较小子问题的结果,并在类似或重叠的子问题中使用它们。
通常,这些算法用于优化。在解决手头的子问题之前,动态算法会尝试检查先前解决的子问题的结果。动态算法的目的是对问题进行整体优化,而不是局部优化。
动态规划算法的重要示例包括:
斐波那契数列
背包问题
汉诺塔
Python - 均摊分析
摊还分析涉及估计程序中一系列操作的运行时间,而不考虑输入值中数据分布的范围。一个简单的例子是在排序列表中查找值比在未排序列表中查找值更快。
如果列表已排序,则数据分布方式无关紧要。但当然,列表的长度会产生影响,因为它决定了算法必须经历多少步骤才能获得最终结果。
因此,我们看到,如果获得排序列表的单个步骤的初始成本很高,则随后查找元素的步骤的成本会大大降低。因此,摊还分析有助于我们找到一系列操作的最坏情况运行时间的界限。摊还分析有三种方法。
会计方法 - 这涉及为执行的每个操作分配一个成本。如果实际操作完成得比分配的时间快,则分析中会累积一些正信用。
势能方法 - 在这种方法中,保存的信用作为数据结构状态的数学函数用于将来的操作。数学函数的评估和摊还成本应该相等。因此,当实际成本大于摊还成本时,势能会下降,并用于利用未来成本较高的操作。
聚合分析 - 在这种方法中,我们估计 n 步总成本的上限。摊还成本是总成本除以步数 (n) 的简单除法。
在相反的情况下,它将是负信用。为了跟踪这些累积的信用,我们使用堆栈或树数据结构。早期执行的操作(如排序列表)具有较高的摊还成本,但序列中较晚的操作具有较低的摊还成本,因为累积的信用被利用了。因此,摊还成本是实际成本的上限。
Python - 算法论证
为了断言某个算法是高效的,我们需要一些数学工具作为证明。这些工具帮助我们对算法的性能和准确性提供数学上令人满意的解释。下面列出了一些可用于证明一个算法优于另一个算法的数学工具。
直接证明 - 它通过使用直接计算来直接验证陈述。例如,两个偶数的和始终是偶数。在这种情况下,只需将您正在研究的两个数字相加并验证结果为偶数即可。
数学归纳法 - 在这里,我们从一个特定的事实实例开始,然后将其推广到所有可能属于该事实的值。这种方法是采用一个经过验证的事实案例,然后证明在相同给定条件下,它对于下一个案例也成立。例如,所有形式为 2n-1 的正数都是奇数。我们证明了它对于某个 n 值成立,然后证明它对于下一个 n 值也成立。这通过归纳证明建立了该陈述通常是正确的。
反证法 - 这种证明基于条件“如果非 A 蕴含非 B,则 A 蕴含 B”。一个简单的例子是,如果 n 的平方是偶数,则 n 必须是偶数。因为如果 n 的平方不是偶数,则 n 不是偶数。
穷举证明 - 这类似于直接证明,但它是通过分别访问每个案例并证明每个案例来建立的。这种证明的一个例子是四色定理。