二阶导数

---

简介

在微积分中，导数是解决问题和微分方程的基本工具。科学家们使用导数作为工具来分析动态系统，以确定变量的变化，并利用这些变化来构建微分方程，并使用积分来预测未来的变化。简单来说，二阶导数是一个函数的两个连续导数，或者说是该函数的一阶导数的导数。在本教程中，我们将学习导数、导数的阶数、二阶导数、参数函数的二阶导数以及一些解题示例。

导数

由实变量组成的函数的导数，衡量该函数的斜率或其值相对于其他变量的变化。输出称为函数值，而输入称为参数。导数用 $\mathrm{\frac{dy}{dx}}$ 表示。也写成 $\mathrm{\frac{d}{dx}(y)}$ 表示 y 相对于 x 的变化。导数给出了函数在图形上的斜率。

导数的阶数

给出函数的斜率，而二阶导数给出例如，测量距离随时间变化的速率，即速度，可以用函数的一阶导数给出，而速度的变化，即加速度，可以用该函数的二阶导数给出。函数的一阶导数可以写成 $\mathrm{\frac{dy}{dx}}$，而二阶导数可以用 $\mathrm{\frac{d^{2}y}{dx^{2}}}$ 表示。一阶导数曲线形状。

二阶导数

一种用于计算阶数为 2 的函数导数的特殊类型的微分方程称为二阶导数。它可以表示为

$\mathrm{y"\:,\:d^{2}y\:/\:dx^{2}\:,\:y"(x )}$

一个具有可变系数的二阶微分方程可以简单地写成 $\mathrm{y"\:+\:p(x)y'\:+\:q(x)y\:=\:f(x)\:,\:Where\:p(x)\:,\:q(x)\:,\:and\:f(x)}$ 是方程中 x 的函数。而对于常系数，它可以表示为 $\mathrm{y"\:+\:py'\:+\:qy\:=\:0}$ 。

参数函数的二阶导数

在某些情况下，使用函数来建立自变量和因变量之间的关系变得复杂。因此，使用第三个变量来简化计算。使用的第三个变量称为参数，表达式称为参数方程。

因此，现在有三个变量 x、y 和 t。由于 t 是参数，它成为自变量，而 x 和 y 成为因变量。因此，x 和 y 表示为 t 的方程。

因此，参数函数的二阶导数可以表示为 -

$$\mathrm{\frac{d^{2}y}{dx^{2}}\:=\:\frac{d}{dx}\:.\:\frac{dy}{dx}(t)}$$

但是当我们应用导数时，函数是变量 t 的函数，我们正在对 x 求导，根据链式法则，项 $\mathrm{\frac{dt}{dx}}$ 会相乘，为了抵消它，我们将乘以 $\mathrm{\frac{dx}{dt}}$。

$$\mathrm{\frac{d^{2}y}{dx^{2}}\:=\:(\frac{d^{2}y}{dx^{2}}\:.\:\frac{dt}{dx})\:.\:\frac{dx}{dt}}$$

解题示例

1. 求解二阶微分方程 $\mathrm{b"\:-\:6b'\:+\:5b\:=\:0}$

解：假设 $\mathrm{b\:=\:e^{ra}}$ 并求其一阶和二阶导数 - $\mathrm{b'\:=\:re^{ra}\:,\:b"\:=\:r^{2}e^{ra}}$

接下来，将 $\mathrm{b,\:b'\:,\:and\:b"\:in\:b"\:-\:6b'\:+\:5b\:=\:0}$ 的值代入

$$\mathrm{r^{2}e^{ra}\:-\:6re^{ra}\:+\:5e^{ra}}$$

$$\mathrm{=\:e^{ra}(r^{2}\:-\:6r\:+\:5)}$$

$\mathrm{=\:r^{2}\:-\:6r\:+\:5}$

$\mathrm{\Longrightarrow\:(r\:-\:5)(r\:-\:1)\:=\:0}$

$\mathrm{\Longrightarrow\:r\:=\:1\:and\:5}$

给定微分方程的解可以表示为 $\mathrm{b\:=\:Ae^{a}\:+\:Be^{5a}}$，因为微分方程的根是实数。

2. 考虑给定的方程 $\mathrm{q"\:-\:8q'\:+\:16q\:=\:0}$ 并求其二阶导数。

解 - 假设 $\mathrm{q\:=\:e^{rp}}$，一阶导数由 - $\mathrm{q'\:=\:re^{rp}}$ 给出，二阶导数由 - $\mathrm{q"\:=\:r^{2}e^{rp}}$ 给出

接下来，将 $\mathrm{q\:,\:q'\:and\:q"\:in\:q"\:-\:8q'\:+\:16q\:=\:0}$ 的值代入 我们有，

$$\mathrm{r^{2}e^{rp}\:-\:8re^{rp}\:+\:16e^{rp}\:=\:=}$$

$\mathrm{\Longrightarrow\:e^{rp}(r^{2}\:-\:8r\:+\:16)\:=\:0}$

$\mathrm{\Longrightarrow\:r^{2}\:-\:8r\:+\:16\:=\:0}$

$\mathrm{\Longrightarrow\:r^{2}\:-\:8r\:+\:16\:=\:0}$

$\mathrm{(r\:-\:4)(\:-\:4)\:=\:0}$

$\mathrm{r\:=\:4\:and\:4}$

给定微分方程的解可以表示为 $\mathrm{q\:=\:Ae^{4p}\:+\:Bpe^{4p}}$，因为微分方程的根是相同的实数。

示例 3：考虑给定的方程 $\mathrm{9q"\:+\:12q'\:+\:29q\:=\:0}$，并求其二阶导数。

解：假设 $\mathrm{q\:=\:e^{rp}}$，一阶导数由 - $\mathrm{q'\:=\:re^{rp}}$ 给出，二阶导数由 - $\mathrm{q"\:=\:r^{2}e^{rp}}$ 给出

接下来，将 $\mathrm{q\:,\:q'\:,\:and\:q"\:in\:9q"\:+\:12q'\:+\:29q\:=\:0}$ 的值代入 我们有，

$$\mathrm{9q"\:+\:12q'\:+\:29q\:=\:0}$$

$\mathrm{\Longrightarrow\:e^{rp}(9r^{2}\:+\:12qr\:+\:29\:=\:0)}$

$\mathrm{\Longrightarrow\:9r^{2}\:+\:12r\:+\:29\:=\:0\:\:\rightarrow\:特征方程}$

$\mathrm{\Longrightarrow\:r\:=\:[\frac{-12\:\pm\:\sqrt{12^{2}\:-\:4\:\times\:9\:\times\:29}}{2\:\times\:9}]}$

$\mathrm{\Longrightarrow\:r\:=\:(-2\:/\:3)\:\pm\:(5\:/\:3)i}$

给定微分方程的解可以表示为 $\mathrm{q\:=\:e^{(-2\:3)x}[A\:\sin\:(5\:/\:3)x\:+\:B\:\cos\:(5\:/\:3)x]}$，因为微分方程的根是复数。

结论

在本教程中，我们学习了微积分和函数的二阶导数及其意义。在微积分中，导数是解决问题和微分方程的基本工具。由实变量组成的函数的导数衡量输出相对于输入的变化。函数的一阶导数可以写成 $\mathrm{\frac{dy}{dx}}$，而二阶导数可以用 $\mathrm{\frac{d^{2}y}{dx^{2}}}$ 表示。一种用于计算阶数为 2 的函数导数的特殊类型的微分方程称为二阶导数。

常见问题

1. 一阶和二阶导数告诉我们关于函数图形的什么信息？

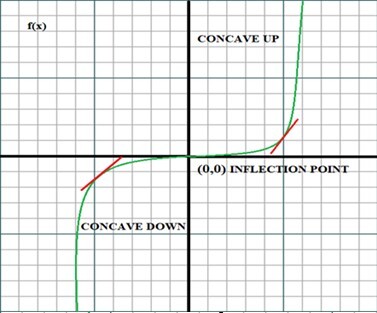
一阶导数给出函数的斜率，如果一阶导数为正，则函数的图形递增，负数表示递减，0 表示中性。而二阶导数给出函数曲线的形状，如果二阶导数为正，则图形向上凹，点为局部最小值，而如果为负，则图形向下凹，点为局部最大值，零表示无凹度，点称为拐点。

2. 定义一个具有常系数的二阶微分方程？

一个微分方程 $\mathrm{y"\:+\:py'\:+\:qy\:=\:f(x)}$，其中 p、q 表示常系数，被称为具有常系数的二阶微分方程。

3. 给出参数函数的二阶导数的方程。

$\mathrm{\frac{dy/dx}{dx/dt}}$ 其中因变量为“x”和“y”，而自变量为“t”

4. 函数的二阶导数中向上凹和向下凹是什么？

如果给定函数的二阶导数大于零，则称为向上凹，如果小于零，则称为向下凹。

5. 什么是拐点？

此点的二阶导数等于零。换句话说，在拐点处既不是向上凹也不是向下凹。