数据结构中虚拟树中的伸展树

在虚拟树中，一些边被视为实线，一些被视为虚线。通常的伸展操作只在实线树中执行。为了在虚拟树中的节点 y 上执行伸展操作，实现了以下方法。

该算法查看树三次，每次遍历一次，并对其进行更改。在第一次遍历中，仅在实线树中执行伸展操作，从节点 y 开始，从 y 到整个树根的路径变为虚线。这条路径通过拼接变为实线。现在，在节点 y 上进行最终的伸展操作将使 y 成为树的根。非正式地说，该算法解释如下

伸展(y) 算法

第一遍 沿着虚拟树向上遍历，但伸展操作仅在实线子树内执行。在这一遍结束时，从 y 到根的路径变为虚线。

第二遍 从节点 y 向上遍历，在 y 的每个真祖先节点处进行拼接。在这一步结束时，从 y 到根的路径变为实线。除此之外，节点 y 及其在原始树（第一遍之前的树）中的所有子节点现在都成为左子节点。

第三遍 从节点 y 向上遍历到根，以正常方式执行伸展操作。

这使我们能够利用先验知识来改进我们的概率估计。对于给定的叶子集。因此，目标是构建一个具有最小外部路径权重的树。

下面给出一个例子

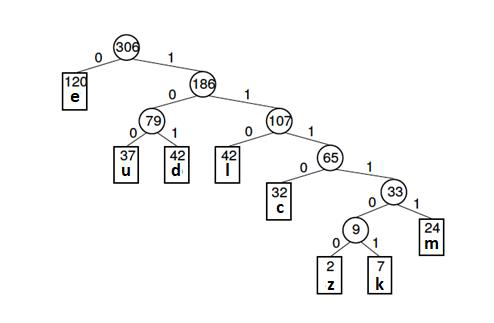
字母频率表

霍夫曼编码

霍夫曼树（以上例为例）如下所示

Arnab Chakraborty

更新于: 2020-01-07

138 次查看

开启你的 职业生涯

通过完成课程获得认证

立即开始