
利用平面展开图求长方体表面积
引言
在本课中,我们将使用立体图形的平面展开图来求立体图形的表面积。
立体图形的平面展开图是将立体图形沿其棱展开,并将各个面以二维图案展开的结果。
长方体的平面展开图由矩形和平方构成。
利用平面展开图求长方体表面积
求出长方体平面展开图中每个矩形和平方的面积,并将这些面积加起来,即可得到棱柱的表面积或总表面积。
例如,如果正方体一个边的长度为4个单位,则其一个面的面积为4 × 4 = 16平方单位。从平面展开图中,我们可以看到共有六个相等的表面,因此总表面积为6 × 16 = 96平方单位。
利用平面展开图求长方体的表面积
长方体或长方体是由如图所示的平面展开图折叠而成的:
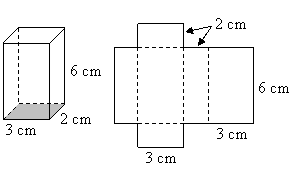
从展开图中我们可以看到,有两个矩形尺寸为3厘米×6厘米,有两个矩形尺寸为2厘米×6厘米,还有两个矩形尺寸为2厘米×3厘米。则总表面积为:
2 × 3 × 6 + 2 × 2 × 6 + 2 × 2 × 3 = 72 cm2
例1
求出给定长方体的表面积(单位:平方厘米)。
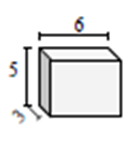
解:
步骤1
利用平面展开图求长方体的表面积
= 2(l w + w h + l h);l = 6;w = 5;h = 3
步骤2
给定棱柱的表面积 = 2(6 × 5 + 6 × 3 + 3 × 5)
= 2(30 + 18 + 15)
= 126 平方厘米
例2
求出给定长方体的表面积(单位:平方厘米)。
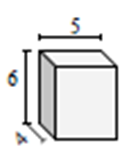
解:
步骤1
利用平面展开图求长方体的表面积
= 2(l w + w h + l h);l = 5;w = 6;h = 4
步骤2
给定棱柱的表面积 = 2(5 × 6 + 5 × 4 + 6 × 4)
= 2(30 + 20 + 24)
= 148 平方厘米
广告