
利用平面展开图求三角柱的表面积
引言
在本课中,我们使用三角柱的平面展开图来求三角柱的表面积。
立体图形的平面展开图是指将立体图形沿着它的边展开,并将它的各个面以二维图案的形式铺展开。
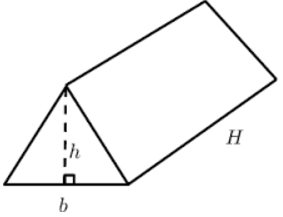
三角柱的平面展开图由矩形和三角形组成。
利用平面展开图求长方体的表面积
求出三角柱平面展开图中每个矩形和三角形的面积,并将这些面积加起来,即可得到三角柱的表面积或总表面积。
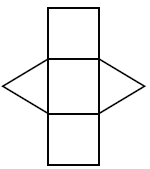
例如,假设一个直角三角形是三角柱的底面,它的两条直角边分别为 3 个单位和 4 个单位,棱柱的高为 10 个单位。从平面展开图中,我们可以看到有两个全等的三角形面和三个矩形面,它们的面积如下:6 平方单位和 (3 + 4 + 5)10 = 120 平方单位。那么棱柱的表面积 = 2(6) + 120 = 132 平方单位。
利用平面展开图求三角柱的表面积
例 1
利用平面展开图求下列三角柱的表面积。
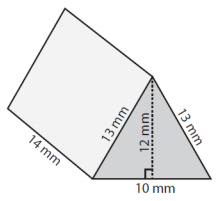
解答
步骤 1
利用平面展开图求三角柱的表面积
三角形底边的边长
a = 13mm;b = 13mm;c = 10mm;高 h = 14mm
三角形面积 = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{18\left ( 18-13 \right )\left ( 18-13 \right )\left ( 18-10 \right )}$
= 60 平方毫米
步骤 2
棱柱的表面积 = 2 × 三角形面积 + h (a + b + c)
= 2(60) + (13 + 13 + 10)14
= 120 + 504
= 624 平方厘米
例 2
利用平面展开图求下列三角柱的表面积。
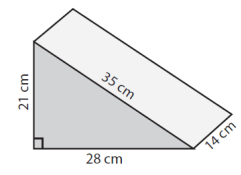
解答
步骤 1
利用平面展开图求三角柱的表面积
三角形底边的边长
a = 21cm;b = 28cm;c = 35cm;高 h = 14cm
三角形面积 = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{42\left ( 42-21 \right )\left ( 42-28 \right )\left ( 42-35 \right )}$
= 294
步骤 2
棱柱的表面积 = 2 × 三角形面积 + h (a + b + c)
= 2(294) + (21 + 28 + 35)14
= 588 + 1176
= 1764 平方厘米