数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学MATLAB中的频域上采样
上采样的介绍
在数字信号处理中，允许提高信号采样率的技术被称为上采样。对于在频域表示的信号，上采样是通过在频域中添加零来实现的。
在数字信号处理中，频域上采样通常用于对数字信号进行插值或扩展带宽。
在MATLAB中，上采样过程分为以下三个阶段
步骤1 - 执行离散傅里叶变换 (DFT)
在这个阶段/步骤中，给定的信号通过对其执行离散傅里叶变换从时域转换为频域。在这个过程中，信号被分解成其基本频率成分。这个分解后的信号表示为复指数函数的和。
DFT运算将一系列离散样本或数字信号转换为一系列复数，称为频谱。频谱指定信号频率成分的幅度和相位。
步骤2 - 执行零填充
在这个阶段，在频域表示的信号中添加一些额外的零。这个过程称为零填充。零填充通过引入新的频率项来增加频谱的长度。因此，它增加了信号的采样率和分辨率。
步骤3 - 执行逆离散傅里叶变换 (IDFT)
此步骤涉及第一步的逆运算，即离散傅里叶变换。执行逆离散傅里叶变换将频域信号转换为时域信号，以获得时域中的上采样信号。此过程根据其频率成分重建原始信号。
这就是我们如何使用MATLAB在频域中执行数字信号的上采样以产生具有更高采样率和更长持续时间的上采样信号。
频域上采样广泛应用于数字信号处理、信号插值、信号重采样等。
现在，让我们讨论一个用于在频域执行上采样的MATLAB程序。
示例
% MATLAB program demonstrate the up-sampling in frequency domain
% Define the original sampling rate
f = 80;
% Create a time vector
t = 0:1/f:1;
% Define the original signal
a = cos(2*pi*50*t);
% Perform the DFT of the original signal
A = fft(a);
% Specify the up-sampling factor
uf = 2; % Adjust as per needs
% Perform zero-padding of the signal in the frequency-domain
upsampled_A = [A zeros(1, (uf-1)*length(A))];
% Perform the IDFT on the zero-padded signal to get the up-sampled signal in time domain
upsampled_a = ifft(upsampled_A);
% Perform the up-sampling of time vector
upsampled_t = 0:1/(f*uf):(1+(1/f)-(1/(f*uf)));
% Plot the original and up-sampled signals
figure;
subplot(2,1,1);
plot(t, a);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');
subplot(2,1,2);
plot(upsampled_t, upsampled_a);
title('Upsampled Signal');
xlabel('Time');
ylabel('Amplitude');
输出
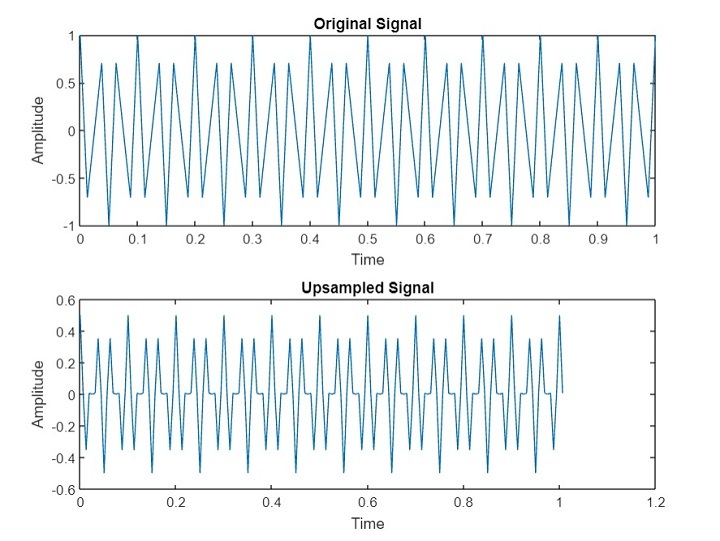
解释
在这个MATLAB代码中，我们演示了在频域中对信号进行上采样的过程。在这个程序中，我们首先定义信号“f”的原始采样率。接下来，我们使用频率“f”创建一个时间向量“t”。该向量从0开始，以“1/f”的速率递增到1。
之后，我们创建原始信号“a”，它是一个频率为“50 Hz”的余弦信号。然后，我们使用“fft”函数对信号“a”执行离散傅里叶变换，以获得复数频谱“A”。接下来，我们指定上采样因子“uf”。在这种情况下，“uf = 2”将使信号上采样2倍。
然后，我们对DFT信号“A”执行零填充，通过添加额外的零来增加其长度。之后，我们使用“ifft”函数对上采样信号执行逆离散傅里叶变换，将其转换回时域，并将结果存储在“upsampled_a”变量中。
接下来，我们对时间向量“t”执行上采样，并将结果存储在“upsampled_t”变量中。这是通过将原始采样率增加上采样因子“uf”来完成的。
最后，我们在一个带有标题“原始信号”和“上采样信号”的图中，在两个子图中绘制原始信号和上采样信号。
因此，这就是我们如何使用MATLAB在频域中对给定信号进行上采样的方法。
浏览量：358
