
- VLSI设计教程
- VLSI设计 - 首页
- VLSI设计 - 数字系统
- VLSI设计 - FPGA技术
- VLSI设计 - MOS晶体管
- VLSI设计 - MOS反相器
- 组合MOS逻辑电路
- 时序MOS逻辑电路
- VHDL编程
- VHDL - 简介
- VHDL - 组合电路
- VHDL - 时序电路
- Verilog
- Verilog - 简介
- 行为建模与时序
- VLSI设计有用资源
- VLSI设计 - 快速指南
- VLSI设计 - 有用资源
- VLSI设计 - 讨论
组合MOS逻辑电路
组合逻辑电路或门,对多个输入变量执行布尔运算,并确定输出作为输入的布尔函数,是所有数字系统的基本构建块。我们将检查简单的电路配置,例如双输入与非门和或非门,然后将我们的分析扩展到多输入电路结构的更一般情况。
接下来,将以类似的方式介绍CMOS逻辑电路。我们将强调nMOS耗尽负载逻辑和CMOS逻辑电路之间的异同,并举例说明CMOS门的优势。在其最一般的形式中,执行布尔函数的组合逻辑电路或门可以表示为多输入、单输出系统,如图所示。
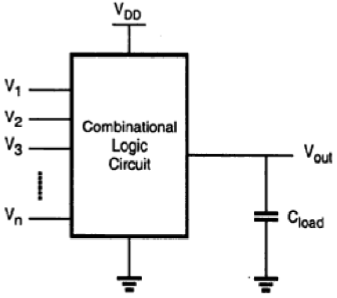
节点电压(相对于接地电位)表示所有输入变量。使用正逻辑约定,“1”的布尔(或逻辑)值可以用VDD的高电压表示,“0”的布尔(或逻辑)值可以用0的低电压表示。输出节点加载了电容CL,它表示电路中寄生器件的组合电容。
CMOS逻辑电路
CMOS双输入或非门
该电路由并联连接的n网络和串联连接的互补p网络组成。输入电压VX和VY施加到一个nMOS晶体管和一个pMOS晶体管的门上。
当一个或两个输入都为高时,即当n网络在输出节点和地之间形成导电路径时,p网络被截止。如果两个输入电压都为低,即n网络被截止,则p网络在输出节点和电源电压之间形成导电路径。
对于任何给定的输入组合,互补电路结构使得输出通过低阻抗路径连接到VDD或接地,并且对于任何输入组合都不会在VDD和地之间建立直流电流路径。CMOS双输入或非门的输出电压将获得VOL = 0的逻辑低电压和VOH = VDD的逻辑高电压。开关阈值电压Vth的方程由下式给出
$$V_{th}\left ( NOR2 \right ) = \frac{V_{T,n}+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}}}$$
CMOS双输入或非门的布局
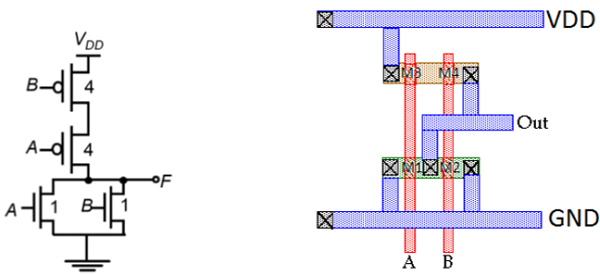
该图显示了使用单层金属和单层多晶硅的CMOS双输入或非门的示例布局。此布局的特征为:
- 每个输入的单根垂直多晶硅线
- 分别用于N和P器件的单个有源形状
- 水平运行的金属总线
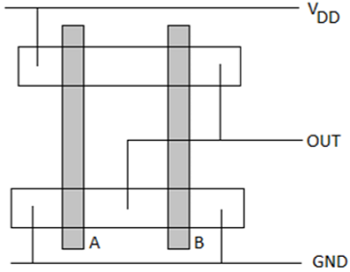
CMOS N0R2门的线框图如下所示;它直接对应于布局,但不包含W和L信息。扩散区域由矩形表示,金属连接和实线分别表示触点,交叉阴影条表示多晶硅柱。线框图可用于规划最佳布局拓扑。
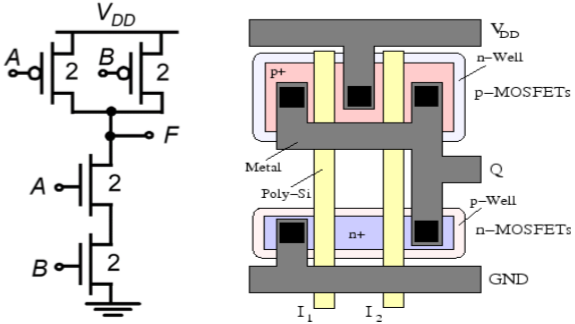
CMOS双输入与非门
双输入CMOS与非门的电路图如下所示。
该电路的工作原理与CMOS双输入或非门的工作原理完全对偶。如果两个输入电压都为逻辑高,则由两个串联连接的nMOS晶体管组成的n网络将在输出节点和地之间形成导电路径。p网络中的两个并联连接的pMOS晶体管都将关闭。
对于所有其他输入组合,一个或两个pMOS晶体管将导通,而p网络被截止,从而在输出节点和电源电压之间形成电流路径。该门的开关阈值获得如下:
$$V_{th}\left ( NAND2 \right ) = \frac{V_{T,n}+2\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+2\sqrt{\frac{k_{p}}{k_{n}}}}$$
此布局的特征如下:
- 用于输入的单根多晶硅线垂直穿过N和P有源区域。
- 单个有源形状用于构建两个nMOS器件和两个pMOS器件。
- 电源布线在布局的顶部和底部水平运行。
- 输出线水平运行,便于连接到相邻电路。
复杂逻辑电路
NMOS耗尽负载复杂逻辑门
为了实现多个输入变量的复杂函数,可以将为或非门和与非门开发的基本电路结构和设计原理扩展到复杂逻辑门。能够使用少量晶体管实现复杂逻辑函数是nMOS和CMOS逻辑电路最吸引人的特性之一。以下面的布尔函数为例。
$$\overline{Z=P\left ( S+T \right )+QR}$$
用于实现此函数的nMOS耗尽负载复杂逻辑门如图所示。在此图中,由三个驱动晶体管组成的左侧nMOS驱动分支用于执行逻辑函数P (S + T),而右侧分支执行函数QR。通过将两个分支并联连接,并将负载晶体管置于输出节点和电源电压VDD之间,我们获得了给定的复杂函数。每个输入变量仅分配给一个驱动器。
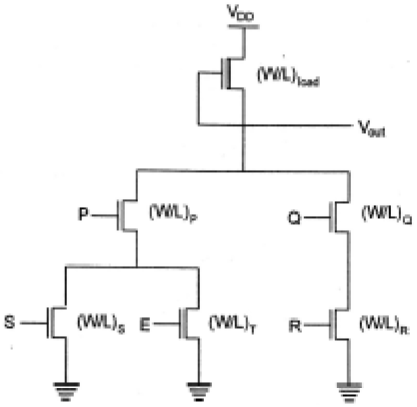
检查电路拓扑结构可以得到下拉网络的简单设计原则:
- 或运算由并联连接的驱动器执行。
- 与运算由串联连接的驱动器执行。
- 反转由MOS电路操作的性质提供。
如果实现该函数的电路中所有输入变量都为逻辑高,则由五个nMOS晶体管组成的下拉网络的等效驱动器(W/L)比率为
$$\frac{W}{L}=\frac{1}{\frac{1}{\left ( W/L \right )Q}+\frac{1}{\left ( W/L \right )R}}+\frac{1}{\frac{1}{\left ( W/L \right )P}+\frac{1}{\left ( W/L \right )S+\left ( W/L \right )Q}}$$
复杂CMOS逻辑门
n网络或下拉网络的实现基于与nMOS耗尽负载复杂逻辑门相同的基本设计原则。pMOS上拉网络必须是n网络的对偶网络。
这意味着nMOS网络中的所有并联连接都将对应于pMOS网络中的串联连接,并且nMOS网络中的所有串联连接都对应于pMOS网络中的并联连接。该图显示了从n网络(下拉)图构建对偶p网络(上拉)图的简单构造。
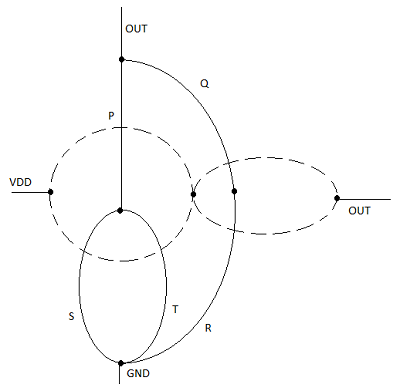
下拉网络中的每个驱动晶体管由ai表示,每个节点由下拉图中的一个顶点表示。接下来,在下拉图中的每个封闭区域内创建一个新的顶点,并且相邻的顶点通过边连接,这些边仅穿过下拉图中的每条边一次。此新图显示了上拉网络。
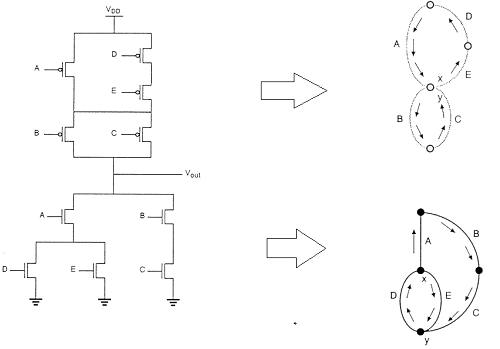
使用欧拉图方法的布局技术
该图显示了复杂函数的CMOS实现及其使用任意门排序完成的线框图,这为CMOS门提供了非常非最佳的布局。
在这种情况下,多晶硅柱之间的间距必须允许它们之间进行扩散到扩散的间距。这当然会消耗相当多的额外硅面积。
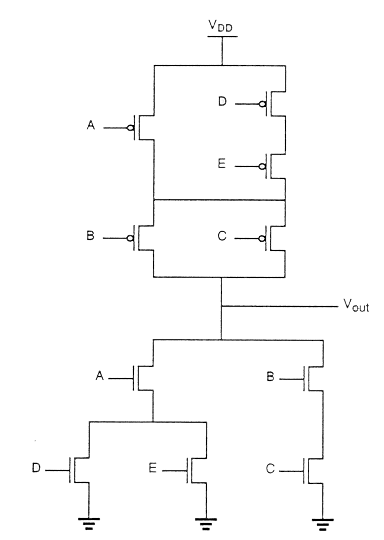
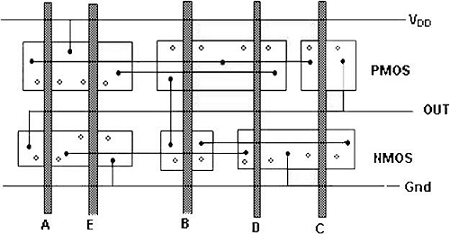
通过使用欧拉路径,我们可以获得最佳布局。欧拉路径定义为一条不间断的路径,该路径恰好遍历图的每条边(分支)一次。在下拉树图和上拉树图中找到具有相同输入排序的欧拉路径。