星形和三角形连接系统中的电压和电流

星形（Y 形）连接系统

设 V_R、V_Y 和 V_B 表示三相电压，而 V_RY、V_YB 和 V_BR 表示线电压。假设系统是平衡的，因此

$$\mathrm{\lvert\:V_{R}\rvert=\lvert\:V_{Y}\rvert=\lvert\:V_{B}\rvert=\lvert\:V_{ph}\rvert}$$

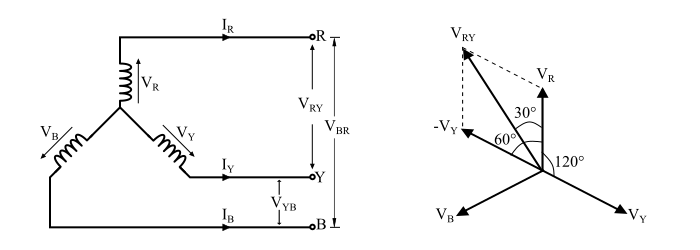
从星形连接负载的电路和相量图可以看出，线电压 V_RY 是 V_R 和 V_Y 的矢量差，或者 V_R 和 –V_Y 的矢量和，即

$$\mathrm{V_{RY}=V_{R}+(-V_{Y})=V_{R}-V_{Y}}$$

应用平行四边形法则得到其大小，我们得到：

$$\mathrm{V_{RY}=\sqrt{V_R^2+V_Y^2+2V_RV_{Y}\cos\:60^{\circ}}}$$

$$\mathrm{\Rightarrow\:V_{RY}=\sqrt{V_{ph}^2+V_{ph}^2+2V_{ph}^2\cos\:60^{\circ}}=\sqrt{3}V_{ph}}$$

同样地，

$$\mathrm{V_{YB}=V_{Y}-V_{B}=\sqrt{3}V_{ph}}$$

$$\mathrm{V_{BR}=V_{B}-V_{R}=\sqrt{3}V_{ph}}$$

$$\mathrm{\because\:V_{RY}=V_{YB}=V_{BR}=V_{L}=线电压}$$

$$\mathrm{\therefore\:V_{L}=\sqrt{3}V_{ph}}$$

因此，在星形连接系统中，

线电压 = √3 × 相电压

再次，参考星形连接系统的电路，可以看出每条线都与其各自的相绕组串联。因此，在星形连接中，每条线的线电流等于相应相绕组中的电流。

设 I_R、I_Y 和 I_B 分别为 R、Y 和 B 线中的电流。由于负载是平衡的，因此，

$$\mathrm{I_{R}=I_{Y}=I_{B}=I_{ph}(假设)}$$

然后，

$$\mathrm{I_{L}=I_{ph}}$$

⇒线电流 = 相电流

注意 – 对于平衡的星形连接系统，线电流的矢量和等于零，

即

$$\mathrm{I_{R}+I_{Y}+I_{B}=I_{n}=0}$$

其中，I_n 是中性线电流。

三角形连接系统

设 I_RY、I_YB 和 I_BR 是三角形连接系统中的相电流，而 I_R、I_Y 和 I_B 是线电流。

通过参考电路和相量图，可以看出每条线中的电流是相应相电流的矢量差，并给出如下：

$$\mathrm{I_{R}=I_{BR}-I_{RY}}$$

$$\mathrm{I_{Y}=I_{RY}-I_{YB}}$$

$$\mathrm{I_{B}=I_{YB}-I_{BR}}$$

现在，电流 I_R 的大小可以通过平行四边形法则求得，如下所示：

$$\mathrm{I_{R}=\sqrt{I_{BR}^{2}+I_{RY}^2+2I_{BR}I_{RY}\cos\:60^{\circ}}}$$

假设系统是平衡的，因此，

$$\mathrm{\lvert\:I_{RY}\rvert=\lvert\:I_{BR}\rvert=\lvert\:I_{YB}\rvert=I_{ph}}$$

$$\mathrm{\Rightarrow\:I_{R}=\sqrt{I_{ph}^{2}+I_{ph}^2+2I_{ph}^2\cos\:60^{\circ}}=\sqrt{3}I_{ph}}$$

同样地，

$$\mathrm{I_{Y}=\sqrt{3}I_{ph}\:\:和\:\:I_{B}=\sqrt{3}I_{ph}}$$

由于系统是平衡的，因此通过每条线的电流将相同，即

$$\mathrm{I_{R}=I_{Y}=I_{B}=I_{L}=线电流}$$

$$\mathrm{\therefore\:I_{L}=\sqrt{3}\:I_{ph}}$$

$$\mathrm{\Rightarrow\:线电流=\sqrt{3}\times\:相电流}$$

由于在三角形连接系统中不存在中性点，因此相电压和线电压相同。参考电路图，

$$\mathrm{V_{RY}=V_{YB}=V_{BR}=V_{L}}$$

$$\mathrm{\Rightarrow\:V_{L}=V_{ph}}$$

Manish Kumar Saini

更新于：2021-07-09

13K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习