数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学一辆以52千米/小时速度行驶的汽车，驾驶员踩下刹车，并以均匀的加速度向相反方向运动。汽车在5秒内停止。另一辆车以3千米/小时的速度行驶，驾驶员缓慢踩下刹车，并在10秒内停止。在同一张图纸上，绘制两辆车的速度-时间图。哪辆车在踩下刹车后行驶的距离更远？
已知：一辆汽车以52千米/小时的速度行驶，驾驶员踩下刹车，并以均匀的加速度向相反方向运动。汽车在5秒内停止。另一辆车以3千米/小时的速度行驶，驾驶员缓慢踩下刹车，并在10秒内停止。
要求：在同一张图纸上绘制两辆车的速度-时间图。找出在踩下刹车后行驶距离更远的汽车。
解题步骤
对于汽车₁
初始速度 u = 52 千米/小时 [已知]
= 52 × 5/18 米/秒 [将千米/小时转换为米/秒]
= 14.44 米/秒
最终速度 v = 0
时间 t = 5 秒
这里：
当 t = 0 时，速度 = 14.44 米/秒，我们假设这是点 A(0, 14.44)。
当 t = 5 时，速度 = 0，我们假设这是点 B(5, 0)。
对于汽车₂
初始速度 u = 3 千米/小时 [已知]
= 3 × 5/18 米/秒 [将千米/小时转换为米/秒]
= 0.83 米/秒
时间 t = 10 秒
最终速度 v = 0
这里：
当 t = 0 秒时，速度 = 0.83 米/秒，我们假设这是点 C(0, 0.83)
当 t = 10 秒时，速度 = 0，我们假设这是点 D(10, 0)
两辆车的速度-时间图：
在坐标图上绘制点 A(0, 14.44) 和 B(5, 0)，我们得到表示汽车₁速度-时间图的线段 AB。
在坐标图上绘制点 C(0, 0.83) 和 D(10, 0)，我们得到表示汽车₂速度-时间图的线段 CD。
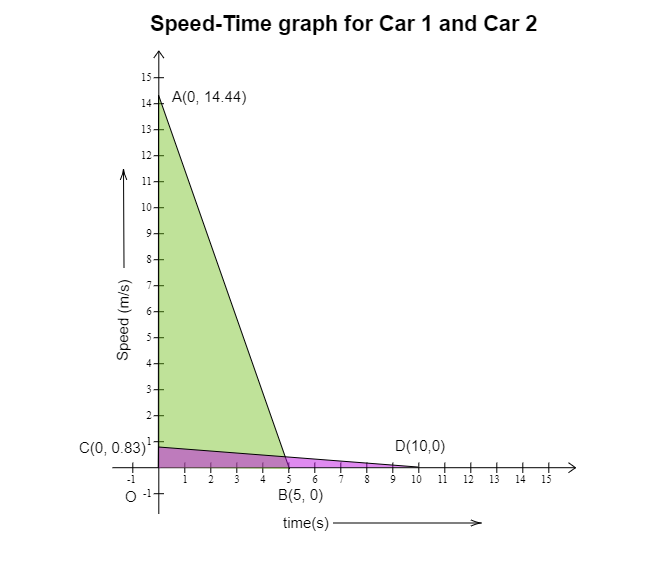
汽车₁行驶的距离 = 三角形 AOB 的面积
= 1/2 × AO × OB
= 1/2 × 14.44 × 5
= 7.22 × 5
= 36.10 米
汽车₂行驶的距离 = 三角形 COD 的面积
= 1/2 × CO × OD
= 1/2 × 0.83 × 10
= 0.41 × 10
= 4.1 米
因此，汽车₁在踩下刹车后行驶的距离更远。
浏览量：153
