圆的几分之几

定义

一个完整的圆圈视为1，圆圈的部分则用分数表示。例如，如果一个圆圈被分成8等份，每一份都表示分数1/8。这样的圆圈的三份就表示3/8，以此类推。
这里我们处理的是一种问题类型，其中给出了表示圆圈中某些部分的分数，我们需要找到表示圆圈中剩余未知部分的分数。为了解决这类问题，我们将表示分数部分的分数加起来，然后从1（整个圆圈）中减去这个和。结果就是表示圆圈未知分数部分的分数。

例题1

未阴影部分占圆圈的多少？请用最简分数表示你的答案。

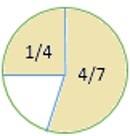
解答

步骤1

首先我们找到图形中阴影部分的总分数。

$\frac{1}{4}$ + $\frac{4}{7}$ = $\frac{7}{28}$ + $\frac{16}{28}$ = $\frac{(7+16)}{28}$ = $\frac{23}{28}$

步骤2

为了找到图形中未阴影部分的分数，我们从1中减去我们得到的结果($\frac{23}{28}$)。

1 − $\frac{23}{28}$ = $\frac{28}{28}$ − $\frac{23}{28}$ = $\frac{(28−23)}{28}$ = $\frac{5}{28}$

所以，图形中未阴影部分的分数是$\frac{5}{28}$。

例题2

阴影部分占圆圈的多少？请用最简分数表示你的答案。

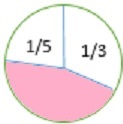
解答

步骤1

首先我们计算图形中未阴影部分的多少。

$\frac{1}{5}$ + $\frac{1}{3}$ = $\frac{3}{15}$ + $\frac{5}{15}$ = $\frac{(3+5)}{15}$ = $\frac{8}{15}$

步骤2

为了找到图形中未阴影部分的分数，我们从1中减去我们得到的结果($\frac{8}{15}$)。

1 − $\frac{8}{15}$ = $\frac{15}{15}$ − $\frac{8}{15}$ = $\frac{(15−8)}{15}$ = $\frac{7}{15}$

所以，图形中阴影部分的分数是$\frac{7}{15}$。