复数的辐角

---

简介

复数的辐角可以描述为复数所形成的直线与阿根图平面的正x轴所成的角。复数的辐角描述了复数的虚部和实部之间的关系。在本教程中，我们将了解复数、复数的极坐标形式、复数的辐角以及一些基于复数的示例。

复数

复数是数系中的元素，由实数和虚数单位 i 组成，其中 i 满足条件：i²=-1。当复数在阿根图平面上绘制时，复数的实部和虚部分别标记在 x 轴和 y 轴上。阿根图平面上的点 X(a, b) 可以表示直线 Z = a + ib，并且直线 OX 与正 x 轴成一定角度。下图显示了给定的复数 Z = a + ib 在复平面上表示。此平面用于表示复数的几何形式。该平面与笛卡尔平面相似，其中 X 轴表示实部，Y 轴表示虚部。

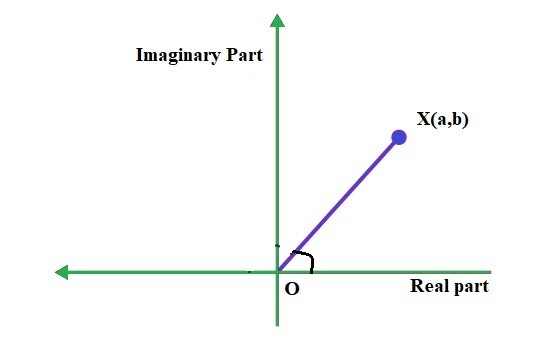
对于复数 Z = a + ib，复数的辐角是角度的度量，它等于复数虚部除以实部所得结果的反三角正切函数。

$$\mathrm{复数的辐角 = θ = Tan^{-1} (b/a)}$$

极坐标形式

复数的极坐标形式可以表示为 A = r(Cosα + i Sinα)。其中角度 α 和 r 分别为复数的辐角和复数的模。它是表示复数极坐标形式的关键方法之一。复数极坐标形式的坐标可以表示为 (rCosα, rSinα)。

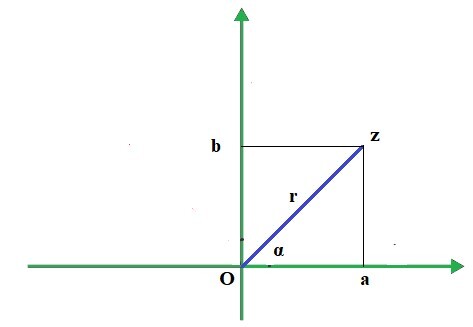
上图显示了在阿根图平面上表示的具有坐标 (a,b) 的复数“z”。角度 α 是该直线与正 x 轴所成的角。

复数的辐角

阿根图平面上的复数可以通过其两个重要特征来定义：复数的辐角和模。可以通过计算复数的模来计算复数坐标到原点的距离。而复数所形成的直线与正 x 轴所成的角则构成复数的辐角。

arg Z 表示复数 Z =x + iy 的辐角。对于由坐标 Z(x, y) 表示的复数 Z = x + iy，以及由 O(0, 0) 表示的直线的原点，直线 OZ 逆时针与正 x 轴所成的角称为复数的辐角。这样由复数 Z = x + iy 形成的角度是虚部与实部形成的分数的反正切函数。

$$\mathrm{复数的辐角 =α = Tan^{-1} (y/x)}$$

例题

1)求下列复数的极坐标形式。

• 3 + 3√3i

• 1+2i.

• 9+9i

答案

a) 令 Z=3 + 3√3i。

根据公式，我们知道方程的实部 x = 3，虚部 y = 3√3

我们知道，复数的辐角可以通过以下公式计算

$$\mathrm{arg (z) = tan^{-1} (y/x)}$$

$$\mathrm{arg (z) = tan^{-1} (3\sqrt{3}/3)}$$

$$\mathrm{arg (z) = tan^{-1} (\sqrt{3})}$$

$$\mathrm{arg (z) = (π/3)}$$

因此，复数的辐角为 π/3 弧度。

b) 令 Z=√3+i

根据公式，我们知道方程的实部 x = √3，虚部 y =1

我们知道，复数的辐角可以通过以下公式计算

$$\mathrm{arg (z) = tan^{-1} (y/x)}$$

$$\mathrm{arg (z) = tan^{-1} (1/\sqrt{3})}$$

$$\mathrm{arg (z) = (π/6)}$$

因此，复数的辐角为 π/6 弧度。

c) 9+9i

根据公式，我们知道方程的实部 x = 9，虚部 y =9

我们知道，复数的辐角可以通过以下公式计算

$$\mathrm{arg (z) = tan^{-1} (y/x)}$$

$$\mathrm{arg (z) = tan^{-1} (9/9)}$$

$$\mathrm{arg (z) = tan^{-1} (1)}$$

$$\mathrm{arg (z) = (π/4)}$$

因此，复数的辐角为 π/4 弧度。

2) 求下列复数的模和辐角。

• 3-4i

• -5i

• -4

解答

我们知道复数的极坐标形式可以表示为

$$\mathrm{A = r(Cosα + iSinα)}$$

其中 r=|Z| 和 α=arg(Z)

a)

$$\mathrm{|Z|=\sqrt{3^2+(-4)^2}}$$

$$\mathrm{|Z|=\sqrt{25}}$$

$$\mathrm{|Z|=5}$$

我们知道 r=|Z|=5

$$\mathrm{α=arg(Z)}$$

$$\mathrm{arg (z) =tan^{-1} (-4/3)}$$

因此，复数的极坐标形式可以写成：

$$\mathrm{A=5 Cos (Tan^{-1} (-4/3))+i Sin(Tan^{-1} (-4/3))}$$

b) $\mathrm{|Z|=\sqrt{0^2+(-5)^2}}$

$$\mathrm{|Z|=\sqrt{25}}$$

$$\mathrm{|Z|=5}$$

我们知道 r=|Z|=5

$$\mathrm{α=arg(Z)}$$

$$\mathrm{arg (z) = tan^{-1} (-5/0)}$$

$$\mathrm{arg (z) = -tan^{-1} \frac{π}{2}}$$

$$\mathrm{arg (z) = -\frac{π}{2}}$$

因此，复数的极坐标形式可以写成：

$$\mathrm{A=5 Cos (-\frac{π}{2})+i Sin(-\frac{π}{2})}$$

c) $\mathrm{ |Z|=\sqrt{4^2+(0)^2}}$

$$\mathrm{|Z|=\sqrt{16}}$$

$$\mathrm{|Z|=4}$$

我们知道 r=|Z|=4

$$\mathrm{α=arg(Z)}$$

$$\mathrm{arg (z) = tan^{-1} (0/4)}$$

$$\mathrm{arg (z) = tan^{-1} π}$$

$$\mathrm{arg (z) =π}$$

因此，复数的极坐标形式可以写成：

$$\mathrm{A=4 Cos (π)+i Sin(π)}$$

结论

复数的辐角可以描述为复数所形成的直线与阿根图平面的正x轴所成的角。复数是数系中的元素，由实数和虚数单位 i 组成，其中 i 满足条件：i²=-1。复数的极坐标形式可以表示为 A = r(Cosα + i Sinα)。可以通过计算复数的模来计算复数坐标到原点的距离。

表达式	含义
Z=a+ib	(a,b) 表示阿根图平面上的坐标。
A = r(Cosα + i Sinα)	表示复数的极坐标形式。
r=|Z|	表示复数的模。
α=arg(Z)	表示复数的辐角。

常见问题

1. 复数辐角的常用范围是多少？

复数辐角的常用范围是 (-π,π)

2. 对于两个复数，arg(Z₁/Z₂) 的值是多少？

根据复数辐角的性质，arg(Z₁/Z₂)=arg(Z₁)-arg(Z₂)

3. 对于两个复数，arg(Z₁×Z₂) 的值是多少？

根据复数辐角的性质，arg(Z₁×Z₂)=arg(Z₁)+arg(Z₂)

4. 在复数形式 Z=a+ib 中，“i” 是什么？

“i” 称为虚数单位。虚数单位表示 -1 的平方根，即 √(-1)

5. 什么是阿根图？

阿根图用于表示复数，其中横轴表示实部，纵轴表示虚部。