复数

---

引言

• 复数使得求负数的平方根变得更简单。

• 复数的概念首次出现是在公元一世纪，当时希腊数学家亚历山大的希罗试图计算负数的平方根。

• 然而，他将整数的负值变为正值，并得到了它们的根值。

• 此外，当十六世纪意大利数学家杰罗拉莫·卡尔达诺发现三阶和二阶多项式的负根时，复数的特性得到了确立。

• 许多科学研究都使用了复数，包括信号处理、电磁学、流体物理学、量子力学和振动分析。

• 在这里，我们将了解复数的定义、术语、可视化、性质和运算。在本教程中，我们将讨论复数。

定义

复数是由实数和虚数组合而成的。复数的格式为$\mathrm{a\:+\:ib}$，其中$\mathrm{ib}$是虚部，a是实部。

因此，复数是两个数（实数和虚数）相加的简单表达式。a是纯实数，b是纯虚数。

• 实数 - 在数系表示法中存在的所有数，例如正数、负数、零、整数、有理数、无理数和分数，都是实数。

• 虚数 - 不是实数的数就是虚数。虚数的平方结果为负数，表示为$\mathrm{i\:=\:\sqrt{-1}}$

虚数单位iota

• iota是虚数单位，用i表示，其值为$\mathrm{\sqrt{-1}}$或$\mathrm{i\:=\:\sqrt{-1}}$

• iota是一个希腊字母，在数学中广泛用于表示复数的虚部。

• 你可能遇到过这种情况：在求解二次方程时，判别式为负数。

• 例如，二次方程𝑥² + 𝑥 + 1 = 0。使用二次方程求解，结果得到一个负的判别式（平方根内的部分）。

极坐标形式

• 复数的极坐标形式以不同于直角坐标形式的方式表示复数。

• 复数是实数和虚数的组合。

• 复数的格式为$\mathrm{a\:+\:ib}$。

• 其中ib是虚部，a是实部。

• 然而，在极坐标形式中，复数表示为模和幅角的组合。

• 复数的模也称为绝对值。这种极坐标形式使用坐标系的实轴和虚轴（虚数）极坐标来表示。

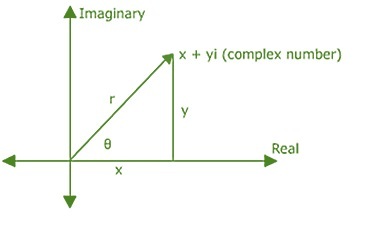
• 这里，垂直轴表示虚轴，水平轴表示实轴。

• 计算r和θ以确定坐标的实部和虚部。r是向量的长度，θ是向量与实轴所成的角。

$$\mathrm{z\:=\:x\:+\:iy}$$

$$\mathrm{z\:=\:r(\cos\theta\:+\:i\:\sin\theta)}$$

对于复数，r表示绝对值或模，角度θ称为复数的幅角，$\mathrm{r\:=\:\lvert\:Z\:\rvert\:=\:\sqrt{x^{2}\:+\:y^{2}}}$

欧拉公式和棣莫弗定理

欧拉公式描述了复指数函数和三角函数之间的关系。

欧拉公式指出：对于任何实数x，$\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\:sin\:x}$

$$\mathrm{z\:=r\:(\:\cos\:x\:+\:i\:sin\:x)}$$

$$\mathrm{z\:=r\:e^{ix}}$$

其中i = 虚数单位，x = 以弧度表示的角度

棣莫弗定理也是用于复数的定理。该定理用于将复数提高到不同的幂。

$$\mathrm{r\:(\cos\:x\:+\:i\sin\:x)^{n}}$$

$$\mathrm{r\:(e^{ix})^{n}}$$

$$\mathrm{=\:r\:e^{ix}}$$

因此，

$$\mathrm{z^{n}\:=\:re^{inx}\:=\:r\:(cos\:nx\:+\:i\:sin nx)}$$

代数形式下复数的平方根

复数的平方根是另一个复数，其平方等于给定的复数。例如，如果复数

$\mathrm{a\:+\:ib}$的平方根是$\mathrm{\sqrt{a\:+\:ib}\:=\:x\:+\:iy}$

两边平方，得到：

$$\mathrm{a\:+\:ib\:=\:(x\:+\:iy)^{2}}$$

$$\mathrm{a\:+\:ib\:=\:x^{2}\:+\:(iy)^{2}\:+\:i2xy}$$

$$\mathrm{a\:+\:ib\:=\:x^{2}\:-\:y^{2}\:+\:i2xy}$$

现在比较实部和虚部

$\mathrm{a\:=\:x^{2}\:-\:y^{2}}$ 和 $\mathrm{b\:=\:2xy}$

我们知道，

$$\mathrm{(x^{2}\:+\:y^{2})^{2}\:=\:(x^{2}\:-\:y^{2})^{2}\:+\:(2xy)^{2}}$$

现在代入它们的值

$$\mathrm{(x^{2}\:+\:y^{2})^{2}\:=\:(a)^{2}\:+\:(b)^{2}}$$

$\mathrm{x^{2}\:+\:y^{2}\:=\:\sqrt{(a)^{2}\:+\:b^{2}}}$ 和 $\mathrm{a\:=\:x^{2}\:-\:y^{2}}$

通过求解这些方程，我们得到

$\mathrm{x\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:+\:a}\:)}{2}}\:and\:y\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:−\:a}\:)}{2}}}$

由于𝑏 = 2𝑥𝑦，所以

如果x和y具有相同的符号，则𝑏 > 0。

如果x和y具有相反的符号，则𝑏 < 0。

因此，复数𝑎 + 𝑖𝑏的平方根由下式给出

$$\mathrm{\sqrt{a\:+\:ib}\:=\:x\:+\:iy}$$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:+\:a}\:)}{2}}\:\pm\:\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:−\:a}\:)}{2}}}$$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{\lvert\:z\:\rvert\:+\:a}{2}}\pm\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{\lvert\:z\:\rvert\:-\:a}{2})}}$$

例题

例1 - 求复数$\mathrm{z\:+\:1\:+\:2i}$的模

解：给定的复数是$\mathrm{z\:+\:1\:+\:2i}$，我们需要求其模，即

$\mathrm{\lvert\:z\rvert\:=\:\sqrt{(1)^{2}\:+\:(2)^{2}}}$

$\mathrm{\lvert\:z\rvert\:=\:\sqrt{5}}$

例2 - 简化复数$\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}}$

解 - 给定的复数是$\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}}$

现在在分子和分母中乘以其共轭复数

$$\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}\times\:\frac{\sqrt2\:-\:i}{\sqrt2\:-\:i}}$$

$$\mathrm{z\:=\:\frac{3\sqrt2\:+\:4\sqrt2i\:-\:3i\:+\:4}{2\:-\:1}}$$

$$\mathrm{z\:=\:{(3\sqrt2\:+\:4)\:+\:i(4\sqrt{2}\:-\:3)}}$$

例3 - 求复数$\mathrm{z\:=\:4\:+\:3i}$的平方根

解 - 给定的复数是$\mathrm{z\:=\:4\:+\:3i}$

$$\mathrm{\lvert\:z\:\rvert\:=\:\sqrt{(4)^{2}\:+\:(3)^{2}}}$$

$$\mathrm{\lvert\:z\:\rvert\:=\:\sqrt{25}}$$

$\mathrm{\lvert\:z\:\rvert\:=\:5}$

并且$\mathrm{a\:=\:4}$，$\mathrm{b\:=\:3}$

现在使用复数平方根的公式

$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{\lvert\:z\:\rvert\:+\:a}{2}}\pm\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{\lvert\:z\:\rvert\:-\:a}{2})}}$

现在代入值

$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{5\:+\:4}{2}}\pm\frac{i3}{\lvert\:3\:\rvert}\sqrt{\frac{5\:-\:3}{2})}}$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\frac{3}{2}\:+\:i)}$$

结论

复数是由虚数和实数相加而成的。复数通常具有$\mathrm{a\:+\:ib}$的形式，并用符号z表示。在这种情况下，由于a和b都是实数，所以用Re(z)表示实部“a”的值，用Im(z)表示虚部“b”的值，ib也被称为虚数。

常见问题

1. 复数是什么意思？

复数是由实数和虚数组合而成的。复数的格式为𝑎 + 𝑖𝑏，其中ib是虚部，a是实部。

2. 在复数中，iota是什么？

iota是虚数单位，用i表示，其值为$\mathrm{\sqrt{-1}}$或$\mathrm{i\:=\sqrt{-1}}$

3. 复数的极坐标形式是什么意思？

与直角坐标形式不同，复数在极坐标形式中以不同的方式表示。复数通常表示为$\mathrm{z\:=\:x\:+\:iy}$

4. 欧拉公式是什么？

欧拉公式描述了复指数函数和三角函数之间的关系。

$\mathrm{z\:=\:r(\cos\theta\:+\:i\:sinx)}$

$\mathrm{z\:=\:r\:e^{ix}}$

5. 复数中的模是什么？

复数$\mathrm{z\:=\:a\:+\:ib}$在阿甘图平面中与原点的距离称为复数的模。它用符号$\mathrm{\lvert\:z\:\rvert}$表示，等于$\mathrm{z\:=\:\sqrt{(a)^{2}\:+\:(b)^{2}}}$。复数的绝对值是表示复数在阿甘图平面中为向量的向量的长度。