复数的极坐标形式

---

简介

复数 $\mathrm{z\:=\:x\:+\:iy}$ 的极坐标形式为 $\mathrm{r(\cos\theta\:+\:i\:\sin\theta)}$。在数学中，有各种坐标系来表示实数。然而，复数系统可以通过两种方式表示，即直角坐标系和极坐标系。在本教程中，我们将学习复数、其极坐标表示以及一些与复数相关的基本公式，并辅以解题示例。

复数

复数是与虚数相关的数系的一种。换句话说，复数是实数和虚数的总和。虚数不过是负整数的平方根。复数通常表示为 $\mathrm{p\:+\:iq}$ 的形式。在这种情况下，p 是实部，q 是虚部。此外，i 是一个虚数，其值为 $\mathrm{\sqrt{-1}}$。一些复数的例子包括 5 + 6𝑖、−3𝑖、−1 + 9𝑖 等。

复数的极坐标形式

在极坐标形式中，复数可以用模和辐角的组合来表示。让我们考虑一个复数，即 $\mathrm{z\:=\:p\:+\:iq}$。给定复数的极坐标形式可以写成

$$\mathrm{z\:=\:r\:(\cos\theta\:+\:i\sin\theta)}$$

其中 $\mathrm{r\:=\:\lvert\:z\:\rvert\:=\:\sqrt{p^{2}\:+\:q^{2}}\:=\:复数的模}$

$\mathrm{p\:=\:r\cos\theta\:,\:q\:=\:r\sin\theta}$

因此，$\mathrm{\theta\:=\:\tan^{-1}(\frac{q}{p})\:=\:复数的辐角}$

极坐标图的表示

让我们考虑一个复数，即 $\mathrm{z\:=\:p\:+\:iq}$。复数在极坐标形式中的图形表示如图所示。

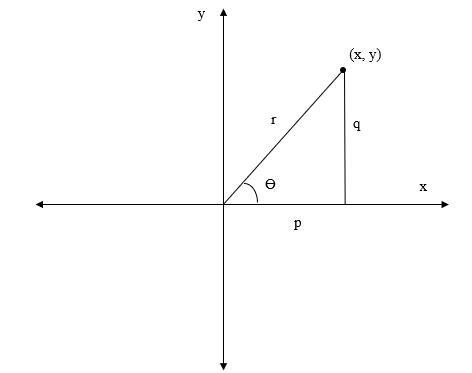
我们可以看到，X 轴表示实部，Y 轴表示复数的虚部。此外，r 是向量的长度，𝜃 是向量与 X 轴所成的角。

现在，使用勾股定理，

$$\mathrm{斜边^{2}\:=\:底边^{2}\:+\:高^{2}}$$

$$\mathrm{r^{2}\:=\:P^{2}\:+\:q^{2}}$$

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{p^{2}\:+\:q^{2}}}$$

同样，$\mathrm{\cos\theta\:=\:\frac{底边}{斜边}\:=\:\frac{p}{r}}$（∵使用三角函数）

$$\mathrm{\Longrightarrow\:p\:=\:r\cos\theta}$$

类似地，$\mathrm{\sin\theta\:=\:\frac{高}{斜边}\:=\:\frac{q}{r}}$（∵使用三角函数）

$$\mathrm{\Longrightarrow\:q\:=\:r\sin\theta}$$

现在，将 p 和 q 的值代入复数的原始方程。我们得到

$$\mathrm{z\:=\:p\:+\:iq\:=\:r(\cos\theta\:+\:i\sin\theta)}$$

得到的表达式是复数的所需极坐标形式。

欧拉公式和棣莫弗定理

欧拉公式建立了复指数与三角函数之间的关系。棣莫弗定理用于将复数提升到不同的幂。让我们详细讨论这两个公式和定理。

欧拉公式

复数的欧拉公式为 $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

让我们推导出这个公式。

欧拉公式的推导 -

$\mathrm{e^{x}}$ 的泰勒级数展开式为

$$\mathrm{e^{x}\:=\:1\:+\:x\:+\:\frac{x^{2}}{2!}\:+\:\frac{x^{3}}{3!}\:+\:\frac{x^{4}}{4!}\:+\:.........}$$

$\mathrm{现在，令\:x\:=\:i\theta}$

因此，$\mathrm{e^{i\theta}\:=\:1\:+\:i\theta\:+\:\frac{(i\theta)^{2}}{2!}\:+\:\frac{(i\theta)^{3}}{3!}\:+\:\frac{(i\theta)^{4}}{4!}\:+\:.........}$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:1\:+\:i\theta\:-\:\frac{\theta^{2}}{2!}\:-\:\frac{i\theta^{3}}{3!}\:+\:\frac{\theta^{4}}{4!}\:+\:.........}$$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:+\:i\:(\theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)}$$

从泰勒级数展开式，

$\mathrm{(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:=\:\cos\theta\:和\:( \theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)\:=\:\sin\theta}$

因此，$\mathrm{e^{i\theta}\:=\:\cos\theta\:+\:i\:\sin\theta}$ 或 $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

棣莫弗定理

与棣莫弗定理相关的公式为

$$\mathrm{(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$$

棣莫弗公式的推导 -

我们将使用数学归纳法的原理来证明上述公式。

令 $\mathrm{Z(m)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$

情况 1 -

考虑 m = 1

$\mathrm{LHS\:=\:(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:(p(\cos\theta\:+\:i\:\sin\theta))^{1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

$\mathrm{RHS\:=\:p^{m}\:(\cos\:m\theta\:+\:i\sin\:m\theta)\:=\:p^{1}\:(\cos\:1.\theta\:+\:i\:\sin\:1.\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

由于 LHS = RHS，因此 Z (m) 对 m = 1 成立。

情况 2 -

假设上述公式对 m = n 成立

因此，

$\mathrm{Z(n)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{n}\:=\:p^{n}(\cos\:n\theta\:+\:i\:\sin\:n\theta)}$

情况 3 -

考虑 $\mathrm{m\:=\:n\:+\:1}$

$\mathrm{LHS\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{m}\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n\:+\:1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n}\:\times\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:p^{n}(\cos\:n\:\theta\:+\:𝑖i\:\sin\:n\theta)\:\times\:p(\cos\:\theta\:+\:i\:\sin\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}(\cos\:n\theta\:.\:\cos\theta\:+\:\cos\:n\theta\:.\:i\:\sin\theta\:+\:i\:\sin\:n\theta\:.\:\cos\:\theta\:+\:\sin\:n\theta\:.\:i\sin\:\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:n\theta\:.\:\cos\:\theta\:-\:\sin\:n\theta\:.\:\sin\theta)\:+\:i(\cos\:n\theta\:.\:\sin\:\theta\:+\:\sin\:n\theta\:.\:\cos\:\theta)]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:(n\theta\:+\:\theta))\:+\:i(\sin\:(n\theta\:+\:\theta))]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos(n\:+\:1)\theta)\:+\:i(\sin(n\:+\:1)\theta)]\:=\:RHS}$

由于 LHS = RHS，因此 Z (m) 对 m = n+1 成立。

因此，上述陈述对于 m 的所有值都成立。

解题示例

1)求给定复数 $\mathrm{2\:+\:2i}$ 的辐角和模。

答案 - 给定的复数为

$$\mathrm{z\:=\:2\:+\:2i}$$

复数的辐角由下式给出

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{2}{2}\:=\:\tan^{-1}\:=\:\frac{\pi}{4}}$$

复数的模由下式给出

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{2^{2}\:+\:2^{2}}\:=\:\sqrt{8}\:=\:2\sqrt{2}}$$

∴ 复数的辐角和模分别为 $\mathrm{\frac{\pi}{4}\:和\:2\sqrt{2}}$

2) 使用欧拉公式将 $\mathrm{7e^{3i}}$ 表示为复数的直角坐标形式 (p + iq)。

答案 - 使用欧拉公式，

$$\mathrm{e^{i\theta}\:=\:\cos\:\theta\:+\:i\sin\:\theta}$$

这里，$\mathrm{\theta\:=\:3}$

因此，$\mathrm{e^{3i}\:=\:\cos\:3\:+\:i\sin\:3\:=\:-0.99\:+\:i(0.14)}$

$$\mathrm{7e^{3i}\:=\:7(-0.99\:+\:i(0.14))\:=\:-6.93\:+\:0.98i}$$

因此，$\mathrm{7\:e^{3i}\:=\:-6.93\:+\:0.98i}$

3) 使用棣莫弗公式确定给定复数的值：$\mathrm{(\sqrt{3}\:+\:i)^{6}}$

答案 - 给定的复数为 $\mathrm{\sqrt{3}\:+\:i}$

我们必须将给定的复数转换为其极坐标形式。

复数的辐角由下式给出

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{1}{\sqrt{3}}\:=\:\frac{\pi}{6}}$$

复数的模由下式给出

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{(\sqrt{3})^{2}\:+\:1^{2}}\:=\:\sqrt{4}\:=\:2}$$

复数的极坐标形式为 $\mathrm{\sqrt{3}\:+\:i\:=\:2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})}$

现在，$\mathrm{(\sqrt{3}\:+\:i)^{6}\:=\:[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}}$

使用棣莫弗公式，

$$\mathrm{[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}\:=\:2^{6}\:(\cos\:\frac{\pi}{6}\:\times\:6\:+\:i\:\sin\:\frac{\pi}{6}\times\:6)}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2^{6}\:(\cos\:\pi\:+\:i\sin\:\pi)\:=\:64\:(-1\:+\:i\:.\:0)\:=\:-64}$$

因此，$\mathrm{(\sqrt{3}\:+\:i)^{6}\:的值为-64}$

结论

本教程简要介绍了复数及其极坐标表示。本教程解释了复数的基本定义及其极坐标表示。此外，还说明了与复数相关的两个重要公式，例如欧拉公式和棣莫弗公式。此外，还提供了一些解题示例，以更好地阐明这一概念。总之，本教程可能有助于理解复数极坐标形式的基本概念。

常见问题

1. 欧拉公式有哪些应用？

欧拉公式被广泛用于确定多面体的边和顶点之间的关系以及追踪单位圆。

2. 我们可以将棣莫弗定理应用于以直角坐标形式表示的复数吗？

是的。但是，复数应首先转换为其极坐标形式。然后，我们可以使用棣莫弗公式确定其值。

3. 复数主辐角的范围是多少？

主辐角的范围在 $\mathrm{-\pi\:到\:\pi}$ 之间。这意味着 $\mathrm{-\pi\:<\:\theta\:\leq\:\pi}$

4. 复数有哪些应用？

复数广泛应用于电路分析、信号处理、量子力学等领域。

5. 复数的模可以为负数吗？

不可以。复数的模是向量的模长。因此，模长始终为正整数。